Точно так же доказываем, что момент относительно начала координат равен

L=QrXlnq*-2q{nq}\dS, (2)

<8)

где S -любая поверхность, взаимно переводимая с поверхностью S, причем в жидкости ие имеется никаких особенностей.

3.64. Импульсивное движение. Предположим, что на движущуюся жидкость действуют внешние импульсы и импульсивное давление.

Если qi -скорость элемента, который ранее двигался со скоростью q, I -внешний импульс, отнесенный к единице массы, и ш -импульсивное давление, то, приравнивая полный импульс изменению количества движения жидкости, ограниченной замкнутой поверхностью S, мы получим, как в п. 3.41,

5ndS-b J iQdx = Q(qi -q)dT. Применяя теорему Гаусса, получаем отсюда

S {lQ-?5-Q(q,-q)}dT-0. Так как объем интегрирования произвольный, то мы имеем

ivS = qi-q.

Это - общее уравнение импульсивного движения.

Это уравнение дает физическую интерпретацию потенциала скоростей следующим образом.

Пусть внешние импульсы отсутствуют и пусть ф - потенциалы скоростей движения, начинающегося из состояния покоя под действием импульсивного давления ш. Тогда в вышеупомянутом уравнении I = О, q = О, qi = - Vф и, следовательно, получим равенство

Vft) = дГф,

которое в случае однородной жидкости приводится к виду

ш = Оф-}-const.

Константой в этом равенстве можно пренебречь, поскольку постоянное давление во всей жидкости ие оказывает никакого результирующего действия на движение, и мы видим, что величина оф является импульсивным давлением, которое мгновенно создает реально существующее движение из состояния покоя (ср. пример 32 гл. 3).

Обратно, движение, возникшее из состояния покоя под действием только импульсивного давления, обязательно является безвихревым, при этом потенциал скоростей равен со/д. Это должно иметь место в том случае, если движение начинается, например, из состояния покоя при внезапном передвижении границ. Доказательство верно также для вязкой жидкости, когда рассматривают только начальное движение (см. фото 1 и 7). Однако вихревые слои (п. 13.70) могут образоваться даже в невязкой жидкости при смыкании слоев жидкости, которые ранее были разделены, а после смыкания движутся с различными скоростями. Наличие даже незначительной вязкости может быть причиной того, что тн слои свертываются и образуют концентрированные вихри (см. фото 1-12).

3.70. Связность. Определение. Область называется связной, если мы можем перейти от какой-либо точки области к другой ее точке, двигаясь вдоль траектории, каждая точка которой лежит в данной области.

Таким образом, внутренняя область сферы (рис. 57), или область между двумя коаксиальными бесконечно длинными цилиндрами (рис. 58), является связной.

Определение. Замкнутая линия, все точки которой лежат в данной области, называется приводимой, если ее можно стянуть в точку области, не выходя за пределы области.

Замкнутая линия PRQS на рис. 57, 58 является приводимой. Линия PRQS на рис. 58 не приводима, так как она не может быть сделана меньше, чем окружность внутреннего цилиндра.

Определение. Область, в которой всякий замкнутый контур приводим, называется односвязной.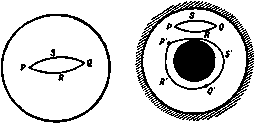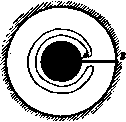

Рис. 57.

Р и с. 58.

Рис. 59.

Примерами односвязных областей являются: внутренняя область сферы; внешняя область сферы; область, внешняя по отношению к некоторому числу сфер; область между двумя концентрическими сферами; неограниченное пространство.

Область между двумя концентрическими цилиндрами на рис. 58, несомненно, не является односвязной, так как она содержит неприводимые замкнутые линии. Однако мы можем сделать эту область односвязной, проводя пере-городку или границу, которая не пересекает сама себя, как, например, плоскость АВ, содержащую образующую каждого цилиндра (рис. 59).

Если провести эту перегородку, то каждая замкнутая линия в видоизмененной области становится приводимой и видоизмененная область является поэтому односвязной.

Кроме того, мы заметаем, что проведение добавочной перегородки между внутренним и внешним цилиндрами разделяет область на две части, из которых каждая в отдельности является связной областью, а в совокупности они не образуют связную область. Таким образом, мы пришли к следующему определению.

Определение. Область называется двусвязной, если она может быть сделана односвязной с помощью проведения одной перегородки. Область называется п-связной, если она может быть сделана односвязной с помощью проведения (п - 1) перегородки.

Примерами двусвязных областей являются: область между двумя коаксиальными бесконечно длинными цилиндрами; область, внутренняя по отношению к тору; область, внешняя по отношению к тору; область, внешняя по отношению к бесконечно длинному цилиндру.

Другая полезная идея содержится в следующем определении.

Определение. Траектории, соединяющие две точки Р и Q области, называются взаимно переводимыми, если одна из них может быть непрерывно деформирована в другую, не выходя из области.

Таким образом, на рис. 57, 58 траектории PRQ, PSQ взаимно переводимы. На рис. 58 траектории PRQ и PSQ взаимно непереводимы. Ясно, что две

взаимно переводимые траектории, взятые вместе, образуют приводимую замкнутую кривую линию.

Определение. Две замкнутые кривые линии называются взаимно переводимыми, если каждая из них может быть непрерывно деформирована в другую, не выходя из области.

Взаимно переводимые кривые линии не всегда являются приводимыми.

Термин взаимно переводимый также может быть применен к поверхности (ср. п. 3.62). Таким образом, поверхности в теореме Стокса, выражаемой формулой (1) п. 2.51, должны быть взаимно переводимыми внутри объема, занятого жидкостью.

Вышеуказанные свойства областей надо называть скорее топологическими, чем просто геометрическими, так как они в основном не зависят от частного вида упоминаемых границ. Например, поперечные сечения цилиндров могут быть эллипсами или какими-либо другими простыми замкнутыми кривыми.

3.71. Ациклическое и циклическое безвихревые движения. Если область, занимаемая жидкостью при безвихревом движении, односвязна, то потенциал скоростей однозначен, так как потенциал скоростей в точке Ропределяется следующей формулой (см. п. 2.52):

фр - S Я^г. (1)

Этот интеграл имеет одно и то же значение для всех траекторий, соединяющих точки Он Р, так как все такие траектории взаимно переводимы. Движение, при котором потенциал скоростей однозначен, называется ациклическим. Следовательно, в односвязной области единственно возможным безвихревым движением является ациклическое. Этот результат существенно зависит от возможности построения поверхности, целиком лежащей в жидкости и содержащей две любые траектории, соединяющие точки О и Р, и последующего применения теоремы Стокса (см. п. 2.52).

Если область не односвязна, то две траектории между точками О и Р могут соединяться поверхностью, целиком лежащей в жидкости, только в том случае, если выполняются некоторые топологические условия. Если это не так, то нельзя сделать необходимого заключения из теоремы Стокса и тогда потенциал скоростей может иметь больше одного значения в точке Р, которое зависит от траектории, соединяющей точку О с точкой Р.

Если потенциал скоростей не однозначен, то говорят, что движение циклическое.

При непрерывном движении жидкости скорость в каждой точке должна быть однозначно определена. Таким образом, даже если потенциал ф имеет более одного значения в данной точке, то градиент Тф должен быть однозначен. Саедовательно, хотя две траектории, соединяющие точки О и Р, могут привести к различным значениям потенциала скоростей фр, эти значения могут отличаться только на скалярную величину х, такую, чтобы Vx = 0. Таким образом, величина х не может зависеть от координат точки Р. Эту скалярную величину можно отождествить с циркуляцией по одному из замкнутых контуров семейства взаимно переводимых, но не приводимых линий. Если С - какая-либо линия, то формула (1) показывает, что циркуляция по С равна уменьшению функции ф при обходе один раз по этому контуру.

Позднее у нас будет возможность рассмотреть отдельные типы циклического движения. Сейчас мы рассмотрим только ациклическое безвихревое движение и общие теоремы, которые будут доказаны применительно только к этому типу движения. Поэтому мы будем рассматривать только односвяз-

ад Глава 3

ные области, но при этом следует также помнить, что ациклическое движение возможно также и в многосвязных областях.

3.72. Кинетическая энергия жидкости. Кинетическая энергия определяется интегралом

взятым по объему V, занимаемому жидкостью. Если движение безвихревое, то

q= -Уф.

Следовательно, если потенциал скоростей ф однозначен, то из условия V\ = 0 и теоремы Грина имеем

(V) (S)

Здесь интегралы берутся по граничной поверхности жидкости, при этом dn обозначает элемент нормали, проведенной внутрь жидкости.

Этот результат имеет простую физическую интерпретацию. Так как действительное движение может возникнуть из состояния покоя под действием импульсивного давления Сф и поскольку -йф/йл -скорость жидкости, нормальная к границе, то величина Офв5( - Vj Зф/йп) - работа, совершенная за единицу времени импульсивным давлением, действующим на элемент 6S в соответствии со следующей теоремой динамики.

Работа, совершенная импульсом за единицу времени, равна произведению импульса на полусумму компонент в его направлении начальной и конечной скоростей точки, на которую он действует. Следовательно, поверхностный интеграл представляет собой работу, совершаемую импульсивным давлением, если движение начинается из состояния покоя.

3.73. Теорема Кельвина о минимуме энергии. Безвихревое движение жидкости, занимающей односвязную область, имеет меньшую кинетическую энергию, чем любое другое движение с теми же самыми нормальными компонентами скорости на границе.

Доказательство. Пусть 7-кинетическая энергия, ф -потенциал скоростей безвихревого движения и Г| -кинетическая энергия какого-либо другого движения, заданного соотношениями

q = - ?Ф + Яо, Vqo = 0, nqo = О на границе.

Второе из этих условий является уравнением неразрывности. Тогда

Г,= J-Je{-Vф + qo)dт=r-t-Гo-5 (Vф)qodт,

где

T-oJ-jOqJrfT.

Теперь заметим, что из формулы {VI) п. 2.34 следует соотношение

V (фqo) = qo(Ф) +Ф (Vqo) = qo (ф). Используя теорему Гаусса и граничное условие nqo=0, получаем

J (Vф)qodт= - 5 n<fqodS = 0.

Таким образом,

Ti = T+To.

Так как Т©-положительная величина, то T<Ti.

3.74. Среднее значение потенциала скоростей. Докажем следующую теорему, полученную Гауссом.

Среднее значение функции ф по любой сферической поверхности, внутри которой 7ф = 0, равно значению этой функции в центре сферы.

Доказательство. Опишем из точки Р сферу S. радиуса г. Тогда по формуле (2) п. 2.63 имеем

(8) (S)

Но второй интеграл, согласно формуле (5) п. 2.62, обращается в нуль. Поэтому

Следствие. Функция ф не моокет иметь ни максимума, ни минимума внутри какой-либо области, в которой V*ф = 0.

Действительно, если бы в точке Р значение фр было максимальным, то оно было бы больше любого значения ф во всех точках достаточно малой сферы с центром в точке Р, а это противоречит только что доказанной теореме.

Теперь мы можем доказать следующую теорему.

При безвихревом двиокении скорость достигает максимального значе-ния на границе.

Доказательство. Возьмем за начало координат точку Р внутри жидкости и проведем ось х по направлению движения в точке Р. Тогда если qp, </о - скорости в точках Р и Q (точка Q лежит вблизи Р), то справедливы равенства

Так как производная dffldx удовлетворяет уравнению Лапласа*), то ее значение в точке Р не может быть ни максимумом, ни минимумом. Следовательно, в непосредственной близости от точки Р имеются точки, такие, как, например, Q, в которых {дч>/дх)1 > (dfffdx)p и, значит, qb > qp.

Таким образом, величина qp ие может достигать своего максимального значения внутри жидкости, поэтому максимальное значение скорости, если таковое имеется, должно достигаться на границе.

Следует заметить, что значение q может быть минимумом внутри жидкости, так как оно равно нулю в критической точке.

Из вышеуказанных результатов мы можем вывести следующую теорему.

При установившемся безвихревом движении гидродинамическое давление имеет минимальное значение на границе.

Доказательство. По теореме Бернулли имеем

4 + 4-9const.

>) Действительно, V А v <p = o.

Таким образом, давление р достигает наименьшего значения там, где q* имеет наибольшее значение, а этого не может быть внутри жидкости. Таким образом, давление р должно достигать минимального значения на границе. Максимального значения давление р достигает в критической точке.

3.75. Среднее значение потенциала скоростей в перифрактической области. Область называется перифрактической), если она изнутри ограничивается одной или более замкнутыми поверхностями. Например, такова область, занятая жидкостью, в которую целиком погружено твердое тело.

Рассмотрим жидкость, покоящуюся в бесконечности и ограниченную изнутри замкнутой поверхностью S и не ограниченную снаружи. Опишем сферу 2 достаточно большого радиуса R с центром в точке Р, окружающую поверхность S. Если движение жидкости безвихревое, то применение теоремы Гаусса к перифрактической области, заключенной между 5 и S, приводит к соотношению

(S) (s)

Следовательно, так как dn= -dR на 2, то получим равенство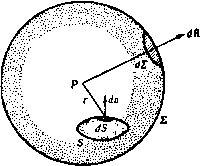

(s) (8)

Рис. 60.

где F -поток внутри рассматриваемой области через внутреннюю границу поверхности S.

Теперь dZ = R}dtu, где d© -телесный угол с вершиной в точке Р, опирающийся на элемент d2. Следовательно, вышеуказанный результат можно записать в виде

d(i)= -

Но если Л1 (ф) -среднее значение ф на сфере 2, то

и, значит,

йЛ<(Ф) F С

где С не зависит от R. Покажем теперь, что С также не зависит от положения центра сферы 2. Для этого переместим центр на расстояние бх, сохраняя R постоянным. Тогда

дС dM(<f) 1 С Эф

4я У дх

dot.

Так как, по предположению, дф/йх->0 в бесконечности, то, делая R достаточно большим, мы сможем сделать dff/dx сколь угодно малым, так чтобы дС/дх=0. Таким образом, С не изменяется, если центр сферы переместить при условии, что поверхность S всегда находится внутри сферы.

) По-гречески яе(}1фООчт(оо - огражденный .

В том случае, когда поверхность 5 является поверхностью твердого тела, сквозь него нет потока жидкости, так что = 0 и, следовательно, среднее значение ф на любой сфере, окружающей твердое тело, постоянно и равно С.

Теперь докажем, что значение фр->С, когда точка Я-оо. В самом деле, применяя результаты п. 2.63 к области между S и S, получаем соотношение

(S) (2)

В силу формул (1) и (2) последний интеграл равен 1

(Г) (2)

Следовательно, получим равенство

4 (<р,-С, = 5 [,(i)-iS.],s. (3)

Если теперь положим, что г-со, то величина 1/л и производная от этой величины по г стремятся к нулю, и, значит, если точка Я->сю, то

фр->С.

3.76. Кинетическая энергия жидкости, занимающей бесконечную область.

При рассмотрении безвихревого движения жидкости, покоящейся в бесконечности и ограниченной изнутри твердым телом S, будем предполагать, что потенциал скоростей ф однозначен. Применяя метод п. 3.72 к области, заключенной между твердым телом S и поверхностью S, окружающей S, мы получим для кинетической энергии жидкости, занимающей эту область, выражение

(S) (2)

Так как внутри области через поверхность S нет потока, то уравнение неразрывности принимает форму [см. уравнение (2) п. 3.20]

(S) (2)

и, следовательно,

(S) (2)

где С -произвольная постоянная. Из уравнения (1) следует, что интеграл {Oiidn)dI, не зависит от Б и равен нулю, так как для твердой границы

интеграл \ {d(f!dn) dS = 0. Следовательно, если мы дадим постоянной С

значение, к которому величина ф стремится в бесконечности, согласно п. 3.75, и затем расширим поверхность Е во всех направлениях, то второй интеграл обратится в нуль и мы получим следующее выражение для кинетической энергии:

(S) (S)

3.77. Теоремы единственности. Докажем теперь некоторые теоремы, касающиеся ациклического безвихревого движения жидкости. Доказательства основываются на следующей эквивалентности выражений для кинетической энергии:

lgJ,dT=-le59dS. (1)

где объемный интеграл берется по всему объему жидкости, а поверхностный интеграл берется по всей границе.

(I) Ациклическое безвихревое движение невозможно в жидкости, целиком ограниченной неподвижными твердыми стенками.

Так как dif/dn = 0 в каждой точке границы, то, следовательно,

qdx = 0. Так как 9? не может быть отрицательно, то q-0 повсюду

и жидкость находится в покое.

(II) Ациклическое безвихревое движение жидкости, ограниченной твердыми стенками, мгновенно прекратится, если стенки привести в состояние покоя.

Это утверждение является непосредственным следствием теоремы (I).

(III) Не может быть двух различных форм ациклического безвихревого движения ограниченной массы жидкости, в которой границы имеют заданные скорости.

Пусть, если это возможно, ф1, фг являются потенциалами скоростей двух различных движений, удовлетворяющими условию д(ру/дп = дц>г/дп в каждой точке границы.

Тогда функция ф=ф1 -Фг является решением уравнения Лапласа и поэтому представляет возможное безвихревое движение, при котором

Эф! . Ф2 Q

дп дп дп

Следовательно, как и в случае (I), q - 0 в каждой точке и, значит, ф1 - ф2 = const, так что движения жидкости по существу одинаковы.

Эта теорема показывает, что безвихревое движение определяется единственным образом, если заданы граничные условия.

(IV) Если данные импулы;ивныг давления прикладываются к границам ограниченной массы жидкости, находящейся в покое, то результирующее движение, если оно ациклическое и безвихревое, определяется единственным образом.

Пусть функции ф1 и фг - потенциалы скоростей двух различных возможных движений жидкости. Импульсивное давление, создающее первое движение, равно Q9i, импульсивное давление, создающее второе движение, равно офг, и так как импульсивные давления задаются на границах, то

Оф1= еф2

в каждой точке границы.

Следовательно, ф = - фг - потенциал скоростей возможного безвихревого движения, такой, что ф = О в каждой точке границы. Таким образом, из формулы (1) вытекает, что q - О в каждой точке жидкости. Отсюда следует, что разность ф, - фг = const, и поэтому движения по существу одинаковы.

(V) Ациклическое безвихревое движение невозможно в жидкости, которая покоится в бесконечности, а изнутри ограничена неподвижными твердыми стенками.

Так как жидкость покоится в бесконечности и нет течения через внутренние границы, то кинетическая энергия по-прежнему задается формулой (1) (см. п. 3.76) и доказательство, следовательно, такое же, как в случае (I).

(VI) Ациклическое безвихревое движение жидкости, покоящейся в бесконечности и ограниченное изнутритвердыми стенками, мгновенно прекращается, если остановить границы.

Это непосредственно следует из теоремы (V).

(VII) Ациклическое безвихревое движение жидкости, покоящейся в бесконечности, обусловленное заданным движением погруженного твердого тела, определяется движением твердого тела единственным образом.

Пусть ф фг - потенциалы скоростей двух различных движений. Граничные условия таковы:

* = на поверхности твердого тела, = 72 = О в бесконечности.

Таким образом, ф = ф, - фг - потенциал скоростей возможного движения, такой, что дф/дл = О на поверхности твердого тела, q = Q ъ бесконечности. Из формулы (1) тогда следует, что = О повсюду, так что ф, - фг = = const и оба движения по существу одинаковы.

(VIII) Если жидкость в бесконечности движется с постоянной скоростью, то ациклическое безвихревое движение, обусловленное зеванным движением погруженного твердого тела, определяется движением твердого тела единственным образом.

Кинематические условия не изменяются, если мы наложим на всю систему твердое тело-жидкость скорость, равную по величине и противоположную по направлению скорости в бесконечности. Это приведет жидкость к состоянию покоя в бесконечности. Тогда результирующее движение определяется теоремой (VII). Возвращаясь к исходному движению, нужно добавить всей системе скорость, равную по величине и направлению заданной скорости в бесконечности.

ПРИМЕРЫ К ГЛАВЕ 3

1. Вывести уравнение неразрывности для несжимаемой жидкости в форме

ди dv , dw li+ ду+-дГ=-

2xuz (дс*-z и

Показать, что и=-, . , , v=-,-s--rL* , =--являются компонентами

скорости возможного движения жидкости. Безвихревое ли это движение?

2. Пусть жидкость движется радиально и скорость и есть функция только от г, t, где г -расстояние от фиксированной точки. Доказать, что уравнение неразрывности имеет вид

3. Пусть каждая частица жидкости движется по сфере. Доказать, что уравнение неразрывности имеет вид

cos е J -l--- (Qqo cos в)+(QQ cos в) = О,

где е. *) -широта и долгота и о. ?а>-соответственно угловые скорости по широте и долготе.

4. Пусть О) -площадь поперечного сечения трубкн тока. Доказать, что уравнение неразрывности имеет вид

д д

аГ (0<а)+-57(о ?)=о.

где ds -элемент дуги нити тока в направлении потока, а q-скорость.

6. Пусть уравнение f (г, 0==0 представляет собой поверхность, всегда состоящую из одиих и тех же частиц жидкости. Показать, что через бесконечно малый промежуток

4-(qV)f=0.

е. Объяснить смысл дифференцирования, следуя за движением частицы жидкости, и иайти условие того, что поверхность F (х, у, г, t)=0 может быть граничной поверхностью. Доказать, что переменный эллипсоид

является возможной формой граничной поверхности жидкости в момент времени /.

7. Некоторое количество жидкости занимает длину 21 прямой трубки малого попе-речного сечения. На жидкость действует сила притяжения, направленная к некоторой неподвижной точке внутри трубки и пропорциональная расстоянию от этой точки.

Определить давление на расстоянии х от указанной неподвижной точки, если ближайшая свободная поверхность находится на расстоянии г.

8. Показать, что в случае цилиндрических координат (см. п. 2.72) ускорение равно

-dr~K~di---Л- j + i- dT-dT

где

dt dt di> Ш дш dx

9. Доказать, что уравнения движения в цилиндрических координатах имеют вид (см. пример 8)

±д££Ях 1 др 4i> 41,

Q дх Л щ е a<i dt ш

I др d

-у а^- 5Г

10. Доказать, что в случае, когда жидкость вращается как твердое тело с постоянной угловой скоростью ш около вертикальной оси (г) и единственной внешней силой является сила тяжести, давление дается формулой

где г -расстояние от осн. Показать, что поверхности равного давления-софокусные параболоиды.

II. Пусть жидкость, содержащаяся в замкнутом круговом цилиндре, вращается около оси цилиндра. Доказать, что уравнение неразрывности и граничные условия удовлетворяются, если взять q = xr, где -угловая скорость, зависящая только от времени, и г-радиус-вектор, измеряемый от точки на оси вращения.

12. Пусть жидкость, рассматриваемая в примере И, выходит из состояния покоя под действием внешних сил, компоненты которых равны ах-Ру, ух+бу, 0. Пусть осью цилиндра является ось г. Написать уравнение движения и доказать, что

=i(Y-P).

dt ~ 2

Доказать также, что давление задается формулой

= 1 2г2 + i (ax --(p-bY) xy-ty*],

где г-расстояние от оси г.

13. Пусть движение жидкости отнесено к подвижной системе координат, вращающейся с угловой скоростью < и движущейся со скоростью и. Показать, что уравнение движения имеет вид

Здесь ar/d< = q-U-mxr, а уравнение неразрывности имеет внд

( !)=

времени Ы, F (r-\-q&t, t-\-&t)=0 и что в этом случае выполняется соотношение