Таким образом, в этом случае L = 5280, М = 2240, Т = 3600. Эти числа L, М, Т мы назовем соответствующими коэффициентами длины, массы и времени для двух систем е;}иниц в том смысле, что результаты измерения этих величин во второй системе переводятся в соответствующие результаты измерения в первой системе посредством умножения на числа L, М,Т.

Коэффициенты размерностей V, А, F производных величин, скорости v, ускорения а и силы / легко получаются из определения этих величин и записываются в виде

V = --. А = Уг, F = MA,

так что в конечном счете коэффициент размерности силы задается формулой F = ML/T\

В общем случае если П|, Пг являются двумя результатами измерений одной и той же физической величины п в двух системах единиц, то мы приходим к следующему коэффициенту размерности:

-! = N = LMr. (2)

Условно будем считать, что данная величина имеет размерность Ц^МУТ. Если х = у = г = 0, тогда п, = 2. так что величина, о которой идет речь, не зависит от выбора единиц, как, например, величина, равная отношению массы машин к массе корабля. В таком случае мы говорим, что величина является безразмерной и представляется отвлеченным числом, значение которого не зависит от выбора единиц измерения. Рассмотрим теперь некоторое соотношение

а = Ьс (3)

между значениями а, Ь, с физических величин в динамической системе, т. е. соотношение, которое не изменяется от выбора системы единиц и которое является вполне закономерным для рассматриваемых величин, измеренных в одной частной системе единиц. Предположим, что величины а, Ь, с имеют размерности (р, q, г), (s, t, и) и {х, у, г) соответственно, и тогда можно записать равенства

a, = aiWM4\ b = b2LmT, Ci=CtLMr. (4)

Теперь соотношение (3) принимает вид ai = 6iCi; подставив сюда величины из равенств (4), получим равенство

a2L>MT = bilMTCiLMor.

Так как соотношение (3) не зависит от выбора единиц, то = biC2, откуда следует соотношение

L>MГ = L*M*T*= или ps + x, q = t+y, r = u + z.

Иными словами, каждый коэффициент размерности основных величин должен входить с одинаковым показателем степени с каждой стороны соотношения (3), т. е. обе части формулы (3) должны быть одинаковой физической размерности.

В системах величин, содержащих как длину, массу, время, так и температуру в качестве основных величин (термодинамические системы), должен быть введен коэффициент размерности температуры (скажем, D).

1.10.Скорссть. Так как рассматриваемая жидкость непрерывна, то мы можем ввести следующее определение: жидкая частица состоит из жидкости, заключенной в бесконечно малом объеме, т. е. в объеме, который можно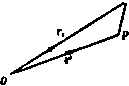

Рис. 2а.

r, = OQ.

Тогда скорость частицы в точке Р определяется вектором *)

Таким образом, скорость q является функцией вектора г и времени /, а именно

q-/(r, /).

Если вид функции / известен, то нам известно и движение жидкости. Чтобы наглядно представить вектор q. проведем через точки пространства небольшие отрезки, имеющие направление этого вектора, v

как показано на рис. 26. \ \ч

Для того чтобы получить физическое представление \ о поле скоростей, определенных вектором q, предположим, что в жидкости расположено большое (но не бесконечно . f большое) число светящихся точек, движущихся вместе с жид- / / / костью. /

Фотография жидкости, снятая за короткий промежуток р 26. времени, показывает, что следы освещенных точек изображаются в виде небольших черточек, длина каждой из которых пропорциональна расстоянию, проходимому точкой за время экспозиции, и поэтому пропорциональна ее скорости. Действительно, такие фотографии являются одним из способов наглядного изображения действительного движения жидкости *).

При помощи фотографий в реальной жидкости можно обнаружить некоторую закономерность поля скоростей, которая выражается в том, что черточки на фотографии образуют части правильных кривых. Тогда такое движение представляет собой движение вдоль линий тока. С другой стороны, такие черточки на фотографиях могут быть нерегулярными, пересекающими друг друга, и тогда движение жидкости называется турбулентным. Предполагается, что движение нашей идеальной невязкой жидкости всегда является движением первого вида. Точное математическое описание турбулентного движения до настоящего времени не получено.

1.11. Линии тока и траектории частиц. Линией тока называется линия, проведенная в жидкости таким образом, что касательная к ней в каждой точке совпадает с направлением скорости жидкости в этой точке.

>) Сведения о векторах подробно излагаются в гл. 2.

) Символ lim следует читать как предел при ti, стремящемся кЬ. Это обычный

метод определения производных, существование которых мы выводим из физических соображений. Символ -* означает стремление к ... . ) См. фото 1 - 12 в начале книгн.

считать настолько малым, что в особых целях его линейными размерами можно пренебречь. Тогда мы можем рассматривать жидкую частицу как геометрическую точку, для того чтобы ввести понятие скорости и ускорения Q частицы.

Рассмотрим частицу, которая в момент времени t находится в точке Р, определяемой вектором (рис. 2а) ):

г = ОР.

В момент времени tt эта частица переместится в точку Q, определяемую вектором

Если скорость жидкости в данной точке зависит не только от координаты точки, но также от времени, то линии тока будут изменяться при переходе от одного момента времени к другому. Таким образом, фотографии, сделанные в различные моменты времени, будут изображать различные системы линий тока. Совокупность всех линий тока в данный момент времени составляет картину течения в этот момент.

Если скорость в каждой точке не зависит от времени, то картина течения будет одинакова в каждый момент времени и такое движение называется установившижя. В связи с этим полезно рассмотреть так называемое относительно установившееся движение. Такое движение возникает в том случае, когда его можно рассматривать как результат наложения постоянной скорости на всю систему, включая наблюдателя. Таким образом, если корабль движется по прямому курсу с постоянной скоростью по невозмущенному морю, то наблюдателю, находящемуся на корабле, поток жидкости, обтекающий корабль, кажется установившимся и он действительно может быть сделан таким при помощи наложения скорости, равной скорости корабля с противоположным знаком, на всю систему, состоящую из корабля и моря.

Рассмотрим движение отдельной частицы жидкости; кривая, которую эта частица описывает во время движения, называется траекторией. Направление движения частицы обязательно должно быть касательным к траектории, так что траектория касается линии тока, проходящей через мгновенное положение частицы, когда она описывает траекторию.

Таким образом, линии тока показывают, как каждая частица движется в данный момент времени.

Траектории показывают, как данная частица движется в каждый момент времени.

Если движение установившееся, то траектории совпадают с линиями тока.

1.12. Трубки тока и струйки тока. Если мы проведем линию тока через каждую точку замкнутой кривой, то получим трубку тока.

Струйкой тока, или элементарной трубкой тока, называется трубка тока, поперечное сечение которой является кривой бесконечно малого размера.

Если движение жидкости зависит от времени, то конфигурация трубок тока и струек тока изменяется от момента к моменту; однако наиболее интересные приложения этих понятий связаны с установившимися движениями жидкости, которые мы сейчас будем рассматривать.

В установившемся движении жидкости трубка тока ведет себя подобно действительной трубке, через которую течет жидкость. Это связано с тем, что не может существовать потока жидкости сквозь стенки трубки тока, так как, по определению, поток всегда касается стенок трубки тока. Кроме того, эти стеики имеют фиксированное положение в пространстве, так как движение установившееся и, следовательно, движение жидкости внутри трубки тока не изменится, если мы заменим стенки твердой поверхностью.

Рассмотрим струйку тока жидкости в установившемся движении. Мы можем считать площадь поперечного сечения струйки настолько малой, что скорость ее будет одинакова в каждой точке сечения, проведенного перпендикулярно направлению скорости.

Пусть теперь qi к - скорости потока в точках, где площади поперечных сечений равны (т, и (Тп (рис. 3). Поскольку жидкость несжимаема, то объем жидкости, вытекающий через одно сечение за данный промежуток времени, должен быть равен объему жидкости, втекающему через другое сечение за то же время. Таким образом, можно записать равенство

Это уравнение представляет собой простейший случай уравнения сохранения массы, или уравнения неразрывности, согласно которому в общем случае движения жидкости количество массы, втекающей в данный объем, должно компенсироваться количеством массы, вытекающей из этого объема. Вышеуказанный результат можно выразить следующей теоремой. . В установившемся двиокении жид-

-----uV-v.----- коста произведение скорости на площадь

.ifr bjT-Z-OJbJ- поперечного сечения постоянно вдоль --~-~/~--- ---- жидкой струйки тока.

Это следует из того, что нить тока р 3 расширяется в местах, где скорость жид-

кости уменьшается, и сужается в местах, где скорость жидкости увеличивается. Другое важное следствие состоит в том, что струйка тока не может оканчиваться внутри жидкости, если скорость не равна бесконечности в соответствующей точке. Если не рассматривать этот случай, то отсюда следует, что вообще струйки тока либо замкнуты, либо оканчиваются на границе жидкости. То же самое справедливо для линии тока, так как поперечное сечение струйки тока можно считать сколь угодно малым.

1.20. Плотность. Если обозначим через М массу жидкости в замкнутом объеме V, то мы можем написать равенство

M=,VQi, (1)

и тогда величина qi является средней плотностью жидкости внутри объема в данное время. В гипотетической непрерывно распределенной среде мы можем определить плотность q как предел величины Qi при V - - 0.

В реальной жидкости, состоящей из большого числа отдельных молекул, мы не можем осуществить предельный переход V -0, так как на некотором этапе в объеме V может не оказаться ни одной молекулы. Поэтому мы будем определять плотность жидкости согласно формуле (1), понимая, что размеры объема V должны быть очень малыми, но такими, чтобы объем V еще содержал большое число молекул. Так, например, в воздухе при обычной температуре приходится около 3 X 10 молекул на кубический сантиметр. Тогда сф1ера радиуса0,001 см содержит около 10 молекул, и, несмотря на малость объема сферы в гидродинамическом смысле, это число молекул достаточно велико для целей измерения средней плотности.

1.30. Давление. Рассмотрим элементарную площадку da, центр которой Р находится в жидкости, и проведем нормаль PN с одной стороны площадки, которую назовем положительной стороной (рис. 4). Другую сторону будем называть отрицательной.

Допустим, что взаимодействие частиц жидкости с обеих сторон от площадки в данный момент времени можно представить при помощи двух равных, но противоположных по направлению сил р da, приложенных к точке Р: при этом каждая сила является давлением, а не растяжением, т. е. жидкость с положительной стороны давит на жидкость с отрицательной стороны с силой pda.

Эксперимент показывает, что в покоящейся жидкости эти силы действуют вдоль нормали; в реальной движущейся жидкости они составляют угол е с нормалью (аналогичный углу трения). Если вязкость жидкости мала, как это имеет место в случае воздуха и воды, то угол е мал. В невязкой жидкости, в которой не возникают касательные напряжения, е = 0, и в этом случае р называется давлением в точке Р.

В вышеприведенном рассуждении не было показано, что давление р не зависит от ориентации элемента da, используемого при определении р. Справедливость этого утверждения доказывается в следующей теореме.

Теорема. Давление в любой точке в невязкой жидкости не зависит от направления.

Доказательство. Пусть PQ - две соседние точки жидкости. Рассмотрим жидкий цилиндр, образующие которого параллельны отрезку PQ и который ограничен поперечным сечением do, и наклонным сечением dca. причем центры этих сечений находятся соответственно в точках Р и Q (рис. 5). Пусть давления в точках Р и Q, определяемые в сечениях doi и dcrj, будут pi .

и рг и пусть нормаль в точке Q образует угол 9 с отрез- /Р^

ком PQ. Объем жидкости в рассматриваемом цилиндре /

равен / doi, где / - бесконечно малая величина. Пусть F является компонентой внешней силы, отнесенной к единице массы жидкости, в направлении PQ,

и / - ускорение цилиндра в направлении PQ. Тогда / если через q обозначить плотность, то на основании / второго закона движения можно записать уравнение

Pi d(Ti - pz doz cos Q + FqI doi /е/ doi.

Рис. 4.

Заметим теперь, что d(T2 cos 9= d(Ti, поэтому, разделив приведенное уравнение на d(Ti, получим уравнение

Pi - P2=lQ(f - f)-

Пусть точка Q приближается к точке Р, тогда отрезок / стремится к нулю и поэтому разность pi - рг также стремится к нулю. Таким образом, если точка Q совпадает с точкой Р, то получаем, что р, = рг. Так как направление нормали к сечению в точке Q совершенно произвольно, то мы заключаем, что

давление в точке Р одинаково при всех ,da, ориентациях определяющего элемента площади.

Давление является скалярной величи-

Fpldo, ной, т. е. не зависит от направления. Размерность давления выражается через коэффициенты размерности (см. п. 1.01) М, L, Т Р яс. 5. массы, длины и времени в следующем виде:

Воздействие жидкости на площадь da, обусловленное давлением, является силой, т. е. это векторная величина, для полного определения которой требуется указать как ее направление, так и величину.

Давление в движущейся жидкости представляет собой функцию времени и координат точки, в которой оно измеряется. Если движение установившееся, то давление может изменяться от точки к точке, но в данной точке оно не зависит от времени.

Стедует отметить, что давление р - существенно положительная величина.

1.40. Теорема Бернулли (специальная форма). В установившемся движении жидкости величина

имеет постоянное значение в каждой точке одной и той же линии тока. Здесь р. Q, - соответственно давление, плотность, скорость; g -ускорение

нию перемещения жидкости.

Работа силы давления в сечении АВ равна p,ai X АА, а ра-бота сил давления в сечении CD равни - PjOj X СС . Следовательно, полная работа сил давления равна разности

Рис. 6. PiOiqi6t - p2f>i-

Жидкость получила кинетическую и потенциальную энергии за счет части жидкости, находящейся между сечениями CD и CD; поэтому полное увеличение количества энергии равно сумме

OtqibtQ Xq\+ a,qi6tQ х ghj.

Жидкость потеряла кинетическую и потенциальную энергии за счет части жидкости, заключенной между сечениями АВ и А'В', т. е. уменьшение количества энергии равно сумме

~ a,<7,6/Q X <7j + a,<7,6/Q х gA,.

Приравнивая величину приращения энергии совершенной работе, получаем уравнение

р,(т,,б/ - ptOtqibt = OtqtbtQ (j<7j + Л, ) - а..в/р (g\+gh, .

Согласно закону сохранения массы (см. п. 1.12), имеем Oi<7, = а2<7 . Подставляя это равенство в предыдущее уравнение, получаем в результате уравнение

Pi-p2 = Q(jq\+ght-Q (y<7l+gA,) .

Поэтому

-f + h\ + Sh.= - + iq\ + gh

так что выражение (p/Q + /tq + gh) имеет одинаковую величину в двух произвольных точках элементарной трубки тока, и поэтому оно одинаково во всех точках линии тока, в которую может быть стянута элементарная трубка тока.

СИЛЫ тяжести и А -высота рассматриваемой точки над фиксированной горизонтальной плоскостью.

Доказательство. Рассмотрим струйку тока, ограниченную сечениями АВ и CD с площадями Oi и а , и пусть pi, qu Ai -давление, скорость и высота в сечении АВ, в то время как Pt, 2. Aj -соответствующие величины в сечении CD (рис. 6). Через короткий промежуток времени Ы жидкость, которая находилась в объеме ABCD, займет объем ABCD, где

AAqtbt, CCqtttt.

При движении жидкости из первого положения во второе будет совершена работа благодаря давлению на сечения АВ и CD. Эта работа расходуется на увеличение кинетической и потенциальной энергий жидкости.

Силы давления на стенки трубки

Р не совершают работы, так как

,3 они перпендикулярны направле-

1.41. Поток в канале. Рассмотрим установившийся поток воды в канале с горизонтальным дном и прямоугольным поперечным сечением ширины Ь. Пусть Л -высота свободной поверхности над дном; поскольку давление на свободной поверхности должно быть равно атмосферному, мы можем из теоремы Бернулли получить уравнение ы*Н-2Л = const, где ы -скорость потока, параллельная стенкам и постоянная по сечению. Если ширина канала мало изменяется, то также мало изменяется скорость и и, следовательно, после дифференцирования вышеуказанного соотношения получим уравнение

udu + gdh = 0.

Кроме того, из уравнения неразрывности следует равенство ubh = const, которое можно представить в виде

du . п

и Ь h

Исключая du из приведенных соотношений, получаем формулу

db ~~ b(gh-u)

Таким образом, глубина и ширина канала увеличиваются одновременно тогда и только тогда, когда ы* < gh, т. е. когда скорость и меньше скорости распространения длинных волн в канале (ср. п. 14.62).

1.42. Замечания о теореме Бернулли. Специальная форма теоремы Бернулли была получена при двух предположениях. Прежде всего мы предполагали, что действует только одна внешняя сила -сила тяжести. Поле силы тяжести является консервативным; это означает, что работа, совершенная силой тяжести при движении тела от точки Р к другой точке Q, не зависит от пути, а зависит только от высоты точки Q по отношению к точке Р. Консервативное поле сил приводит к понятию потенциальной энергии, которая измеряется работой, совершенной телом при переходе от одного определенного положения к другому. Для того чтобы потенциальная энергия единицы массы в точке могла иметь определенный смысл, очевидно, необходимо, чтобы работа сил поля не зависела от пути, по которому совершается переход в эту точку.

Гравитационное поле, очевидно, является самым важным из консервативных силовых полей, но оно является не единственно возможным полем такого вида; например, электростатическое поле также консервативно. Если в более общем случае мы обозначим через Q потенциальную энергию единицы массы в консервативном поле сил, то теорему Бернулли можно сформулировать в более общей форме: выражение

f + j + q

имеет постоянное значение вдоль линии тока. Доказательство проводится тем же методом, что и для специального случая теоремы Бернулли.

Второе предположение состояло в том, что жидкость несжимаема и имеет постоянную плотность. В более общем случае для баротропного потока, т. е. когда давление является функцией плотности *), теорема

1) Это равносильно предположению, что существует уравнение состояния вида f (р. в, S) = 0, где энтропия S имеет повсюду одинаковое значение [так называемый гомэнтропнческий случай (см. п. 20.01).

принимает следующую форму: выражение

имеет постоянное значение вдоль линии тока. Эта форма теоремы Бернулли Доказывается в п. 1.61.

1.43. Константа в теореме Бернулли. Для отдельной линии тока, обозначенной индексом I, теорема Бернулли утверждает, что выполняется соотношение

f+ у9* + гЛ = Сь

где величина Ct постоянная для этой линии тока. Если мы возьмем вторую линию тока, обозначенную индексом 2, то получим соотношение

f + Y4 + gh = C2,

где величина Сг постоянная вдоль второй линии тока.

Мы не доказывали (и в общем случае это неверно), что Ci = Ci. Однако если движение безвихревое (значение этого термина будет объяснено далее в п. 2.41), то константа одинакова для всех линий тока, так что справедливо соотношение

- + ig + gh = C.

где С имеет одно и то же значение в каждой точке жидкости. Позже (см. п. 3.64) также будет показано, что этот случай имеет место всякий раз, когда невязкая жидкость приводится в движение обычным механическим способом, как это происходит, например, при внезапном или медленном движении границ, при открывании отверстия в замкнутом сосуде или при движении тела через жидкость.

1.44. Гидродинамическое давление. При установившемся движении жидкости теорема Бернулли позволяет еще больше выяснить характер давления. В покоящейся жидкости в каждой точке имеется гидростатическое давление рн, и закон Архимеда утверждает, что на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной им жидкости. Частицы жидкости также подчиняются этому закону, и поэтому они находятся в равновесии под действием гидростатического давления рн и силы тяжести. Отсюда следует, что величина рн/Q + gh является константой во всей жидкости. Если жидкость движется, то подъемная сила еще действует, так что если мы напишем

Р = Ро + Рн,

то теорема Бернулли дает и, следовательно,

J + lg = C, (1)

где С' = С-(ря/е + Л) -новая константа.

Формула (1) выражает теорему Бернулли для случая отсутствия силы тяжести.

Величину ро можно назвать гидродинамическим давлением, или давлением, обусловленным движением. В дальнейшем будет установлено, что знание гидродинамического давления позволит вычислить результирующее действие жидкости на погруженное тело; вначале мы должны определить только воздействие, обусловленное давлением Ро, и добавить результат действия давления ря, известного из законов гидростатики. Это очень важный результат, используя который мы можем пренебречь внешней силой тяжести при исследовании многих задач.

Часто считают, что гидродинамические задачи, в которых пренебрегают внешними силами, имеют искусственный и непрактический характер. На самом деле это не так. Пренебрежение внешними силами является только способом избежать ненужные осложнения при исследовании гидродинамических задач. Следовательно, нужно помнить, что если мы пренебрегаем внешними силами, то мы вычисляем действие гидродинамического давления.

Из формулы (1) мы видим, что гидродинамическое давление больше там, где скорость меньше, а также что наибольшее гидродинамическое давление имеет место в точках с нулевой скоростью.

Однако необходимо отметить, что применение способа гидродинамического давления может быть оправдано только в том случае, если границы жидкости неподвижны, так как только при этих условиях гидродинамическое давление постоянно в данной точке. Если жидкость имеет колеблющуюся свободную поверхность, то гидростатическое давление в фиксированной точке будет изменяться и мы должны будем рассматривать полное давление.

В случае сжимаемых жидкостей давление, обусловленное движением, обычно называют аэродинамическим давлением.

1.50. Трубка Пито. На рис. 7. показана заостренная изогнутая трубка ABCD, имеющая отверстие в точке А и запаянная в точке D; U-об-разная часть трубки заполнена жидкостью.

Рис. 7.

Р и с. 8.

Если этот прибор поместить в установившийся поток жидкости и направить открытым концом вверх по течению, то ось горизонтальной части фигуры образует часть линии тока, проходящей через точку А. (11едовательно, если pi -давление в точке А с внутренней стороны трубки и р -давление впереди А, то, согласно теореме Бернулли, справедливо равенство

поскольку жидкость внутри трубки находится в покое. Давление pi измеряется разностью уровней ртути в точках В и С, если предположить, что в части трубки CD имеется вакуум. Описанный прибор представляет собой простейшую форму трубки Пито для определения величины p-f-QV2.

На практике часто требуется измерить величину скорости д, а для *того мы должны иметь способ измерения давления р.

В

Р и с. 9.

Эту величину можно измерить посредством прибора, показанного на рис. 8 и отличающегося от прежнего только тем, что в точке А трубка запаяна, а в точке £, расположенной вблизи от точки А вниз по течению, имеется отверстие. Теперь линии тока идут по стенкам трубки от точки А, и если жидкость в трубке находится в покое и давление непрерывно, то давление вне трубки в окрестности точки £ равно давлению внутри

трубки в точке £ и это давле-

и не измеряется разностью уров-

- ней ртути в точках G и £. На

а-- практике полезно комбинировать

обе трубки в один прибор, как показано на рис. 9.

В этом приборе разность уровней ртути в точках В и G определяет величину pi -p = Q<?/2. Вышеприведенное описание только иллюстрирует принцип измерения скоростей при помощи трубки Пито. Действительный прибор нужно очень тщательно сконструировать, чтобы его влияние на измеряемый поток было как можно меньше. При соответствующем конструировании и аккуратном обращении трубкой Пито можно измерять соответствующие величины с точностью до 1% относительно их истинных значений как в случае воздуха, так и в случае воды.

1.60. Работа газа при расшнреннн. Пусть S и S- поверхности, ограничивающие единицу массы газа до и после малого расширения. Пусть dn -нормальное перемещение элемента dS поверхности о (рис. 10).

Предположим, что давление газа равно р. Тогда работа, совершенная

газом, выразится в виде pdS-dn = pdv, где - объем, ограниченный

поверхностью S; d -увеличение объема v. Но поскольку рассматриваемая масса газа равна единице, то имеем vq=\.

Следовательно, совершенная газом работа равна pd(l/Q), и если в процессе расширения плотность изменяется от значения q до значения Qo, то со-

вершенная работа равна Ц pd При этом мы

р

предполагаем, что давление является функцией только плотности.

Внутренней энергией единицы массы газа будем называть работу, которую единица массы газа для заданного соотношения между р и е может совершить при расширении из его действительного состояния до некоторого начального состояния, характеризуемого величинами Ро и Qo-Обозначая через £ внутреннюю энергию единицы массы газа и интегрируя по частям полученное выше выражение, приходим к соотношению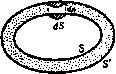

Рис. 10.

Таким образом, получим окончательный вид для внутренней энергии

бо С J