Итак, внутренняя энергия является одним из видов энергии деформации, аналогичной энергии растянутой упругой нити.

1.61. Теорема Бернулли для сжимаемой жидкости. При выводе теоремы Бернулли в случае сжимаемой жидкости мы используем точно такой же метод, как в случае несжимаемой жидкости, однако в данном случае должна быть учтена внутренняя энергия газа.

Используя рис. 6 и обозначая через е, и Qa плотность в сечениях АВ и CD, работу, совершенную давлением, выразим в следующем виде:

Эта работа расходуется на приращение кинетической энергии, потенциальной энергии и внутренней энергии. Таким образом, мы получим уравнение

-\- EiOiqiitQi - £iOi<7i6/qi,

где £i, £0 обозначает внутреннюю энергию единицы массы соответственно в сечениях АВ и CD.

Так как движение жидкости установившееся, то количество втекающей массы через сечение АВ должно равняться количеству массы, вытекающей через сечение CD, и, следовательно, уравнение неразрывности запишется следующим образом:

Поэтому, подставляя уравнение неразрывности в предыдущее уравнение, получаем формулу

\q\ + gh + E..-(Jq\-\-gh-\-E, .

Заменяя в этой формуле значения внутренней энергии, согласно п. 1.60, следующими соотношениями:

Qo Q2 i Q Qo Qi J

Po Po

мы получаем в результате уравнение Бернулли

]f+hl+sf.=]f+iql+ghi. (1)

Если учесть выражение для аэродинамического давления, согласно п. 1.44, теорема Бернулли примет форму

Н- Y (7 = const вдоль линии тока, (2)

отк\да получаем соотношение

dp=-Qqdq. (3)

1.62. Применение теоремы Бернулли к адиабатическому расширению.

Ксли газ расширяется адиабатически (т. е. без изменения количества тепла), то давление и плотность связаны соотношением

p = xev, (1)

Если мы обозначим через ро давление торможения, т. е. при скорости, равной нулю*), и пренебрежем действием силы тяжести, то получим формулу

Y-1 в + 2 q0

так что

Теперь из формулы (1) следует соотношение

PoQ су-1 \poJ

Как известно из теории звуковых волн (см. п. 14.87), скорость звука Сд при давлении Ро задается формулой

г YPo

Следовательно, из формулы (2) мы получаем и поэтому

i=[-(i) r--k.ir+k)+-

Отношение третьего члена ко второму в этом разложении равно 9V4cJ, так что если даже скорость q равна половине скорости звука, то это отношение равно Vie. Таким образом, оказывается, что мы можем с хорошим приближением отбросить все члены, начиная с третьего члена, даже если отношение д/Сд не очень мало. Тогда теорема Бернулли для воздуха примет форму

00 2 - 00

означающую, что воздух можно рассматривать как несжимаемый в очень большом диапазоне скоростей. В частности, для скорости около 500 км/час ошибка, сделанная при измерениях скорости с помощью трубки Пито (см. п. 1.50), составит около 2%.

1) Не доказано, что в жидкости достигается нулевая скорость. Тем не менее давление Ро определяется единственным образом с помощью последующего уравнения.

где X и Y-константы. Для сухого воздуха у =1.405. Следовательно,

Так как величина ро/бо относится к начальному состоянию, то она является константой и, следовательно, из теоремы Бернулли получим соотношение

Кроме того, скорость потока в окрестности крыла самолета будет сравнима со скоростью набегающего потока, и поэтому эффект сжимаемости мал для малых значений скоростей набегающего потока. С другой стороны, сжимаемостью нельзя пренебречь вблизи концов лопастей пропеллера.

1.63. Дозвуковой н сверхзвуковой потоки. Если с -скорость звука, а р -давление, то, согласно п. 14.87, c = yp/Q и, следовательно, из формулы (2) п. 1.62 получим соотношение

с* . 1

2 V -y-l

показывающее, что величина с имеет максимальное значение Со при = 0 и что величина д имеет максимальное значение тах при с = 0, задаваемое формулой

Ятях -

Скорость 9* будем называть критической скоростью, если скорость звука и скорость потока равны, и, следовательно, из соотношения (1) получим формулу

9* = с*=Со/. (3)

Отметим еще следующий вид уравнения Бернулли:

C* = -Jr(Y-l)(7max-<? (4)

(у -С2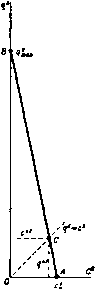

Р и с. 11.

График величины как функции с представляет собой прямую линию АВ на рис. И. Из этого следует, что вдоль линии тока с<Со, дКдтах- Прямая линия д^ - с^ = 0 пересекает прямую АВ в точке С{с*, д*), где д* = с*. Две части АС и ВС этой прямой соответствуют двум физически различным режимам. Если ввести число Маха

M = -f (6)

в каждой точке отрезка АС, то мы имеем д < д* =с* < с, так что М< 1 при условии, что д <с; поток, для которого М < 1, называется дозвуковым.

В каждой точке отрезка ВС мы имеем д > д* =с* > с, так что М > 1, и тогда говорят, что поток сверхзвуковой.

Из формулы (1) мы получаем соотношение

i+4(v-i)M = f=(sO- = (t)

1.64. Газовый поток в сужающейся трубке. Если ш -площадь малого сечения трубки, то трубка будет сужаться, если величина (о уменьшается, когда мы идем вдоль трубки, т. е. если daldsQ, где ds -элемент длины трубки. Из уравнения неразрывности (uQ7 = const следует дифференциальное уравнение

\ dq . \ dq 1 dco

Q ds* q ds~ to ds

Запишем теорему Бернулли для адиабатического закона

-=co rf.

Отсюда следует уравнение

= 0.

Пусть c* = YP/q обозначает местную скорость звука, т. е. скорость в рассматриваемой точке. Тогда

1 dq

Q ds ~ ds

Подставляя в формулу (I) приведенные уравнения, получаем соотношение

♦ds ct-qt\ Ш ds )~ CO ds )

И, таким образом, dqlds положительно, если М< 1, т. е. если q<c.

Следовательно, скорость потока увеличивается по мере уменьшения сечения трубки, если поток дозвуковой; для свер.хзвукового потока скорость уменьшается при уменьшении сечения трубки.

1.70. Трубка Вентури. Принцип трубки Вентури иллюстрируется на рис. 12. Прибор используется для измерения параметров течения в трубе. Он состоит из конической части, которая сужается от полного сечения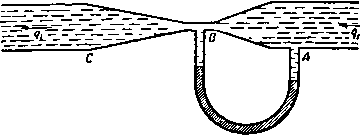

Рис. 12.

трубки в точке А до минимального сечения в точке fl, и из постепенно расширяющейся части, переходящей в точке С снова в трубку с полным сечением. Постепенное расширение части ВС обеспечивает плавное изменение линий трка.

Манометр, имеющий U-образную форму и содержащий ртуть, соединяется с трубкой через отверстия в точках Л и 5; разность уровня в манометре измеряет разность давления в точках Л и В. Пусть величины р„ q\\ Pii qt означают давления и скорости соответственно в точках А и В. Тогда из теоремы Бернулли следует соотношение

Пусть Sj, Sj -площади поперечных сечений в точках А н В. Тогда

= qSi,

так как одинаковый объем жидкости протекает через каждое сечение в данное время. Поэтому для величины <7, получается следующее выражение:

а -л / (Р'-Рг)

в которое подставляется измеренное значение величин Pi - P2-

Если Л -разность уровней ртути в двух частях манометра и а -плотность ртути, то последняя формула принимает вид

где /С -константа прибора.

1.71. Измерение скорости течения газа трубкой Веитури. Предполагая справедливость адиабатического закона для газа в области от входа в трубку до наименьшего сечения, из теоремы Бернулли и уравнения неразрывности получаем соотношения

у Pi I 1 V Рг , j. i

Y-l Qi 2 >~Y-1 Qz 2 V

откуда легко находим формулу

2У f Pi Рг\ - V-VQi 02 У

\Q2J SI

Так как pi/p2 = (61/62)1 TOi следовательно,

2У PL [ ifP2. y-l е, l v Pi У

Для использования этой формулы мы должны знать величины Р(, рг и с,. Поэтому прибор должен быть изменен таким образом, чтобы отверстия в точках i4 и 5 на рис. 12 соединялись с отдельными манометрами; тем самым измерялись бы сами давления pi, рг, а не их разность, как в случае жидкости. Для скоростей, значительно меньших скорости звука, можно использовать обычную формулу и метод, пригодный для жидкости (см. п. 1.62).

1.80. Истечение из отверстия. Если сделать малое отверстие в стенке большого наполненного жидкостью сосуда, то оказывается, что на коротком расстоянии от стенки вытекающая струя жидкости сужается до некоторого минимального поперечного сечения (рис. 13). В самой узкой части вытекающая струя имеет форму цилиндра и все линии тока здесь парал-лБльны между собой. Если о, -площадь отверстия и Oj -площадь минимального поперечного сечения струи, то величина а = : а, называется коэффициентом сжатия. Точное значение коэффициента сжатия может

быть строго вычислено только в некоторых специальных случаях, но можно с достаточной убедительностью показать, что а > Va- То, что а < 1, следует из экспериментально установленного факта существования сужения.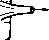

Р 11 с. 13.

1.81. Теорема Торичелли. Пусть на рис. 14 h обозначает глубину caMoii сжатой части струи по отношению к уровню верхней поверхности жидкости

ра, -

А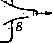

Рис. 11.

в сосуде, наполненном водой, и пусть И - атмосферное давление. Если (7 -скорость истечения в самой сжатой части, то теорема Бернулли даст соотношение

П , , П , 1 о

так как скорость на свободной поверхности воды в сосуде практически равна нулю, а давление на свободной поверхности и на границах свобод-нон струи равно П. Поэтому

g=2gh.

Это соотношение выражает теорему Торичелли для скорости истечения.

Если Сто - площадь поперечного сечения струи в самом сжатом месте, то количество жидкости, вытекающей в единицу времени, равно 02} 2gh.

В большинстве случаев достаточно взять в качестве h глубину отверстия, так как самое сжатое место струи находится вблизи от него. Если IT, площадь отверстия и а - коэффициент сжатия, то количество жидкости, вытекающей за секунду, равно аа, ] 2gh.

1.82. Коэффициент сжатия. Пусть в стенке сосуда, наполненного жидкостью, сделано малое отверстие АВ и пусть Л - глубина отверстия под свободной поверхностью. Пусть И - атмосферное давление, (7 -скорость истечения в самой сжатой части струи. Пусть i4S- проекция площади отверстия на противоположную стенку, при этом обе стенки предполагаются вертикальными.

Если р -гидростатическое давление в отверстии АВ, когда отверстие закрыто, то воздействие отверстий АВ и А'В' на жидкость будет состоять из двух равных по величине, но противоположных по направлению сил ро,. Когда отверстие открыто, то сила pOi в отверстии АВ исчезнет и заменится силой n<Ti. Если мы в первом приближении предположим, что гидростатическое давление остается неизменным, кроме давления у отверстия АВ,

Рис. 15.

Рис. 16.

ТО сила, приводящая в движение жидкость, равна (р -n)oi. Величина количества движения вытекающей жидкости равна Qqoq, где Oj -площадь самого сжатого сечения. Таким образом^), получим соотношение

(р-П) о, = 0207*. С другой стороны, из теоремы Бернулли имеем

Следовательно, 02 = ai/2 и коэффициент сжатия равен /г.

Теорема Бернулли также показывает, что если отверстие открыто, то давление на стенки в окрестности отверстия АВ будет падать ниже гидростатического давления, так что движущая сила действительно больше, чем р -П и, следовательно, вообще Oj/a, > >/г (см. п. 3.32).

Однако если мы сделаем маленькое цилиндрическое сопло, вдающееся внутрь сосуда, то сделанное в начале предположение будет выполняться почти точно и коэффициент сжатия будет равен Va- Это устройство известно как насадок Борда (рис. 15).

С другой стороны, круглый насадок, выступающий наружу (рис. 16), приводит к увеличению потока жидкости, так как самая сжатая часть будет иметь место в выходном отверстии, и мы получим

и, следовательно.

1 р-CTjii/CTi

2 ~р^П~

что превышает предыдущую величину.

Теорема Торичелли показывает, что количество жидкости, вытекающей м единицу времени, увеличивается с ростом коэффициента сжатия, так что iTO приспособление увеличивает истечение. Этот факт был использован древними римлянами, когда население могло потреблять столько воды, сколько можно было извлечь за данное время, применяя истечения из отверстий.

1.90. Теорема Эйлера о количестве движения. Рассмотрим трубку тока, ограниченную поперечными сечениями АВ и CD соответственно с площа-

) В п. 3.40 будет показано, что если движение установившееся, то поток измеряет скорость изменения количества движения

дями ai И в случае установившегося движения жидкости. Пусть gi и 9г -скорости в сечениях АВ и CD, тогда теорема Эйлера утверждает, что если пренебречь массовыми силами, то результирующая сила, обусловленная давлением окружающей жидкости на стенки и концы трубки, эквивалентна силам QOiJ и 0Огд\, приложенным к концевым сечениям АВ и CD и направленным по внешним нормалям к ним (рис. 17).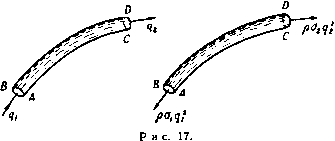

Доказательство. О)гласно второму закону движения Ньютона, результирующая сила должна вызвать изменение количества движения жидкости, занимающей в данный момент времени t часть трубки между сечениями АВ и CD, изображенными на рис. 6.

В момент времени t + bt эта часть жидкости будет занимать часть трубки между сечениями А'В', CD. Таким образом, количество движения рассматриваемой жидкости увеличивается на количество движения жидкости, заключенной между сечениями CD и CD, и уменьшается на соответствующую величину для жидкости между сечениями АВ и А'В'.

Следовательно, за время б/ имеет место увеличение количества движения на величину Q02gt X дг при прохождении через сечение CD и потеря его на величину QOi,6/ X gt при прохождении через сечение АВ. Следовательно, за единицу времени количество движения увеличится на величину оог* в сечении CD и уменьшится на величину QOi в сечении АВ. Эти изменения обусловлены только давлениями на стенки и концевые сечения трубки. Следовательно, давления должны быть эквивалентны силам QOiq/[ и QOzq, приложенным в сечениях АВ п CD и направленным по внешним нормалям к ним.

1.91. Сила, действующая на стенки тонкой трубки. Рассмотрим установившееся движение жидкости в части АВ трубки, площадь поперечного сечения которой настолько мала, что жидкость можно рассматривать как часть элементарной трубки тока (рис. 18).

(Р}*РЧ}

Рис. 18.

Пусть через (Ti, pi, gi обозначены площадь поперечного сечения, давление и скорость в точке i4; через Ог, Рг, дг - соответствующие величины в точке В. По теореме Эйлера о количестве движения, полное действие давления на жидкость в трубке АВ состоит из нормальных сил QOig] в точке А и еог^ в точке В, причем обе силы направлены по внешним нормалям. Однако силы, обусловленные давлениями в точках А и В, равны piOi и ргОг, и обе силы направлены по внутренним нормалям.

Следовательно, силы, действующие на жидкость со стороны стенок вместе с нормальными, направленными внутрь силами piOi, ргг, эквивалентны нормальным, направленным наружу силам QOif, QOzq.

Таким образом, силы, действующие со стороны стенок на жидкость, эквивалентны нормальным, направленным наружу силам Oi (pi + q) в точке i4 и 02 (P2+Q) в точке В. По принципу действия и противодействия силы, действующие со стороны жидкости на стенки трубки, получаются заменой последних на противоположные и поэтому эквивалентны вышеупомянутым нормальным силам, но направленным внутрь.

1.92. Парадокс Даламбера. Рассмотрим длинную прямую трубку, по которой течет невязкая жидкость с постоянной скоростью U. Если в середине трубки мы поместим препятствие А (рис. 19), поток вблизи препятствия изме-

Рис. 19.

нится, но на большом расстоянии как вверх, так и вниз по течению поток останется невозмущенным. Чтобы препятствие находилось в покое, в общем случае к нему необходимо приложить силу и пару сил. Обозначим через F компоненту силы в направлении, параллельном течению. Парадокс Даламбера состоит в том, что в указанных условиях компонента силы F в направлении потока равна нулю. Докажем это.

При доказательстве мы будем пренебрегать массовыми силами, такими, как сила тяжести. Тогда F является результирующей сил давления, действующих на границу препятствия А.

Рассмотрим два поперечных сечения Si и S 2 на большом расстоянии от А вверх и вниз по потоку. Жидкость, заключенная между этими сечениями, может быть разделена на элементарные трубки тока, к каждой из которых применима теорема Эйлера о количестве движения. Наружные элементарные трубки тока ограничиваются стенками трубки, и на них компоненты давления перпендикулярны течению. На струйки тока, находящиеся в соприкосновении с препятствием А, действует твердое тело с силой, составляющая которой в направлении потока равна -F. По теореме Эйлера, результирующая всех давлений на жидкость равняется сумме

которая обращается в нуль, так как Si = S 2-

По теореме Бернулли, давление pi в сечении Si равно давлению р2 в сечении 5 Тогда из уравнения

PiSi - /= - P2S 2 = О

получим требуемое равенство

F = 0.

Если предположить, что стенки трубки удалены, то это будет соответствовать случаю тела, погруженного в неограниченный во всех направлениях поток и, согласно вышеуказанному доказательству, по-прежнему F = 0.

Наконец, если мы наложим на всю систему постоянную скорость U в направлении, противоположном направлению течения, то жидкость на большом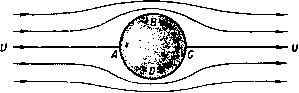

Рис. 20.

Центральная линия тока, идущая со стороны набегания потока, встречает препятствие в точке Л, где жидкость покоится. Точка А, в которой скорость течения равна нулю, обычно называется критической точкой.

Центральная линия тока в точке А раздваивается на части ABC и ADC, соединяющиеся в точке С. Эта точка является второй критической точкой, в которой скорость равна нулю; далее рассматриваемая линия тока сходит с препятствия и удаляется в бесконечность'). Линии тока, примыкающие к центральной, искривлены вблизи сферы и постепенно распрямляются при удалении от нее. Если мы будем удаляться от сферы, то линии тока будут все менее и менее искривленными, так что на большом расстоянии в поперечном направлении от ЛС их кривизна становится пренебрежимо малой. Фотография, снятая в начальной стадии движения, согласуется с рассмотренным качественным описанием (см. фото 1).

В реальной жидкости, такой, как вода, обязательно имеет место внутреннее трение. Эксперимент показывает, что жидкость, непосредственно прилегающая к препятствию, примыкает к поверхности препятствия. В соответствии с этим Прандтль ввел гипотезу пограничного слоя, состоящую в том, что непосредственно к сфере прилегает тонкий слой жидкости, в котором касательная составляющая скорости быстро увеличивается от нуля до ее значения, равного скорости в основном потоке вне сферы; при этом давление изменяется непрерывно в направлении внешней нормали. Если скорость потока увеличивается, то пограничный слой остается тонким в точке Л и на передней стороне сферы, но на противоположной стороне сферы толщина слоя увеличивается, как это иллюстрируется рис. 21 (см. также фото 3).

Внутри пограничного слоя возникает обратное течение с вихрями, в то время как вне пограничного слоя существует описанное выше теоретическое движение. Пограничный слой, таким образом, отделяется от сферы в окрестности точки В.

Если скорость потока продолжает увеличиваться, то точка отрыва пограничного слоя передвигается вперед по направлению к критической точке

*) Мы будем применять термин бесконечность для обозначения области, точки которой удалены от препятствия на такое расстояние, где возмущающее действие препятствия на поток пренебрежимо мало.

расстоянии ОТ препятствия будет находиться в состоянии покоя и препятствие А будет двигаться с постоянной скоростью U. Наложение постоянной скорости не изменит динамических условий. Следовательно, сопротивление тела, движущегося с постоянной скоростью в неограниченной невязкой покоящейся жидкости, будет равно нулю.

1.93. Поток за препятствием. Рассмотрим сферу (рис. 20), обтекаемую потоком, равномерным на большом расстоянии от сферы, и пренебрежем внешними массовыми силами. Тогда линии тока должны быть симметричными относительно диаметра сферы АС, совпадающего с направлением течения.