примеры

И пограничный слой утолщается, переходя в вихревую дорожку, в которой энергия непрерывно уносится вихрями вниз по течению (рис. 22).

При движении сферы в неподвижной жидкости картина относительного движения будет такая же, как описано выше, и сфера будет испытывать лобовое сопротивление, которое компенсирует потери энергии при обтекании. Для поддержания скорости движения необходимо непрерывно сообщать телу энергию.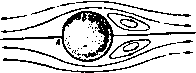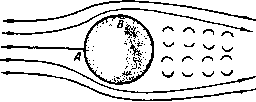

Рис. 21.

Рис. 22.

и парадокс Даламбера не имеет места. Общая справедливость гипотезы Прандтля достаточно хорошо подтверждается фотографиями потока и тем самым показывает, что теоретическая гидродинамика может быть полезной, так как течение вне следа согласуется с теоретическим движением. С другой стороны, теорию мы можем применить к изучению поведения хорошо обтекаемых тел, у которых разрушение пограничного слоя происходит в^пизи кормовой части и соответственно ширина следа за телом будет меньше. Примерами таких хорошо обтекаемых тел являются тело рыбы, специально спроектированные крыловые профили, стойки, имеющие сечения с небольшим лобовым сопротивлением.

В заключение отметим следующие два соображения, которые позволяют применять теорему Бернулли при измерениях в реальной жидкости. Во-первых, отверстия трубки Пито расположены спереди, где пограничный слой тонкий, и, во-вторых, давление не претерпевает разрыва при переходе через этот тонкий пограничный слой.

ПРИМЕРЫ К ГЛАВЕ 1

1. Водяной кран с диаметром 0,6 см расположен на 18 м ниже уровня резервуара, который снабжает водой город. Найти количество воды, вытекающей через кран за один час.

2. Вода бьет струей через маленькое отверстие в большом сосуде, в котором давление 51 атм поддерживается сжатым воздухом; при этом внешнее давление равно 1 атм. Пренебрегая разностью уровней между отверстием и свободной поверхностью воды в сосуде, вычислить скорость, с которой вода вытекает через отверстие.

3. Вдоль горизонтальной трубки переменного поперечного сечения течет установившийся поток воды. Зная, что давление равно 700 мм рт. ст. (удельный вес ртути 13,6) в том месте, где скорость равна 150 см/сек, требуется найти давление в том месте, где пиперечное сечение трубки равно удвоенной ее ширине, принимая =981 см/сек^.

4. Поток в горизонтальной трубе после прохождения самого узкого места, где пло-щ,1дь поперечного сечения равна А, течет при атмосферном давлении в участке трубы с площадью поперечного сечения, равной В. Показать, что если трубку присоединить

трубе в первом указанном месте, то вода будет всасываться через нее в трубу из резервуара, расположенного на глубине 5*(1М'-l/B*)/2g ниже трубы; здесь S-секундный расход воды.

5. Жидкость плотности Q течет вдоль горизонтальной трубки переменного поперечного сечения, и трубка связана с дифференциальным прибором, измеряющим давление

двух точках i4 и В. Показать, что если p\ - pz давление, указанное прибором, то масса т жидкости, протекающей через трубку в одну секунду, задается формулой

где а| и 02->соответственко поперечные сечения в точках А к В.

36 Глав I

6. Сосуд в форме полого кругового конуса с вертикальной осью и вершиной, обращенной вниз, открытый сверху, наполнен водой. Круглое отиерстие, диаметр которого равен 1/ч диаметра основания конуса (п пелнко), открывается в вершине конуса. Показать, что время, необходимое для того, чтобы уровень воды упал до величины, отвечающей половине первоначального объема Л, не может быть меньше чем

(42-1) Yh

7. Жидкость, в которой плотность и давление связаны адиабатическим соотношением p/QV = const, вытекает через тонкую трубку, выходящую из широкого замкнутого сосуда, в котором давление в п раз прспышает атмосферное дапленне р. Показать, что скорость V истечения жидкости задается формулой

(Y-i)e

где с-плотность н самом сжатом месте.

8. Газ, в котором aab.ienne и плотность связаны адиабатическим соотношением р = = aq, течет вдоль трубы. Доказать, что величина

постоянна, если пренебречь массовыми силами, причем q -скорость. Если в направлении потока поперечное сечение трубы уменьшается, то доказать, что скорость q будет увеличиваться и отношение plq будет уменьшаться в направлении потока при условии, что < YP-

9. Показать, что скорость q газа, текущего в тонкой трубке, поперечное сечение которой равно ст, в точке па расстоянии s, измеряемом по дуге от фиксированного поперечного сечения, удоилетаоряет уравнению

d / q\ d

где с-скорость звука п газе и рассматриваемой точке; при этом предполагается, что газ удовлетворяет адиабатическому закону.

10. Если газ вытекает из сосуда через ма.юе отверстие из области с давлением р\ в область с давлением Рг, то доказать, что количество газа, вытекающее в секунду, равно

где p = *Q, щ - площадь сечения в самом сжатом месте (\ - УРг102. (ср. п. 1.64); при этом 02 - плотность в самом сжатом месте.

11. Пусть со-малая площадь поперечного сечения трубки тока в газе; доказать, что qQi>i = comi вдоль трубки тока; используя результат п. 1.64, доказать, что величина <щ максимальна, если (/ = с, и что о) тогда имеет минимальное значение.

12. Если cm -скорость звука в минимальном поперечном сечепии из примера И, то доказать, что имеется верхний предел значения скорости q, даваемый формулой

13. Газ вытекает из точки по радиусам симметрично во всех направлениях, причем давление и плотность удовлетворяют закону р = хо. Пусть т -секундный расход, предполагаемый постоянным; доказать равенство

4л9л2 = m ехр - .

де -скорость на расстоянии г и tj-скорость при о-1.

г лава 2 ВЕКТОРЫ

2.10. Скаляры и векторы. Отвлеченные числа и физические величины, для полного определения которых не требуется задавать направления в пространстве, называются скалярными величинами, или просто скалярами. Например, скалярами являются объем, плотность, масса и энергия. Давление жидкости также является скаляром. Однако сила, действующая на бесконечно малую площадку вследствие давления на нее со стороны жидкости, не является скаляром, так как для полного описания этой силы должно быть задано направление, по которому она действует.

Векторной величиной, или вектором, называется величина, для полного определения которой необходимо задать как число, так и направление в пространстве; эта величина при сложении подчиняется правилу параллелограмма, а при умножении подчиняется законам, которые будут сформулированы позднее. Примерами векторов служат скорость, количество движения, сила. Угловая скорость и момент количества движения также являются векторами, что доказывается в курсах механики.

Вектор может быть полностью представлен отрезком прямой, проведенной в направлении этого вектора. Длина отрезка в выбранном масштабе равна величине вектора. Направление вектора можно обозначить стрелкой на конце отрезка.

В некоторых случаях вектор необходимо рассматривать вместе с некоторой линией, вдоль которой этот вектор направлен; такие векторы называются скользящими. Например, ясно, что при вычислении момента силы существенно положение линии действия силы.

Однако во многих случаях мы будем иметь дело со свободными векторами, т. е. векторами, которые полностью определяются величиной и направлением и которые, следовательно, могут быть изображены в любом удобном нам положении. Так, если мы хотим найти только величину и направление равнодействующей нескольких данных сил, то мы можем использовать силовой многоугольник, не обращая внимания на действительное положение в пространстве линий действия данных сил.

Мы будем обозначать вектор жирной прямой латинской буквой, а его величину той же курсивной буквой. Так, если q - вектор скорости, то его величина обозначается через q. Аналогично вектор угловой скорости © имеет величину (D.

Единичным вектором называется вектор, величина которого равна единице. Любой вектор может быть представлен произведением числового (скалярного) множителя и единичного вектора, параллельного данному вектору. Так, если ia - единичный вектор, параллельный вектору а, то справедливо равенство

a = aia-

Ниже мы рассмотрим некоторые свойства векторов, имея в виду их гидродинамические приложения.

В дальнейшем будем предполагать, что величина вектора отлична от нуля, если специально не оговорено противоположное.

2.11. Скалярное произведенне двух векторов. Пусть а и b - два вектора с величинами анЬ, направленные вдоль лучей OA и ОВ, выходящих из точки О (рис. 23). Пусть угол между этими векторами, т. е. угол АОВ, который считается положительным в направлении наименьшего вращения от а к Ь, равен 6.

Тогда скалярное произведение векторов аЬ определяется соотношением

аЬ = аЬ cos 6.

Рис. 23.

Скалярное произведение векторов является скаляром и измеряется произведением ОА-ОМ, где Л1 -проекция точки В на прямую 0А\ тогда

OA = а, ОМ = b cos 6. Из определения сра-В зу же следует равенство

Ьа = Ьа cos (- 6) = а6 cos 0= ab,

так что порядок сомножителей оказывается несущественным. Если векторы перпендикулярны, то cos 6 = О и аЬ = 0. Обратно, это равенство означает, что или а и b перпендикулярны, или а = О, илиЬ = 0. ЕслиаЬ= О, причем Ъ - произвольный вектор, то а = 0, так как а не может быть перпендикулярным каждому вектору Ь. Если 6 -тупой угол, то скалярное произведение отрицательно. Если ia -единичный вектор, то скаляр iab=bcos6 является составляющей вектора b в направлении некоторого вектора, параллельного ia. Если о и ь -единичные векторы, то iaib=cos6, где 0 -угол между любыми двумя векторами, параллельными и \ь.

Если точка приложения силы F движется со скоростью v, то мощность, которую развивает сила F, равна Fv.

2.12. Векторное произведение двух векторов. Пусть угол между векторами а и Ь, величины которых равны соответственно а я Ь, равен 6 (рис. 24). Положительное направление отсчета угла выбирается от а к Ь.

Мы определим векторное произведение а X Ь как вектор, величина которого а.Ь равна a6sin9 и который перпендику-

р и с. 24.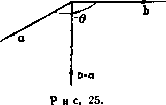

лярен обоим векторам а и Ь, а направлен в ту сторону, откуда вращение от вектора а к вектору b соответствует правилу правого винта .

Из определения следует, что векторное произведение не коммутативно так как 6а sin ( - 6)= -aftsin6 (рис. 25), т. е.

ахЬ=-Ьха.

Если векторы параллельны (6 = 0 или л), мы имеемаХЬ=0. Обратно, это равенство означает, что или векторы а и b параллельны, или один из них равен нулю.

В качество примера рассмотрим движение точки Р твердого тела, которое вращается вокруг неподвижной точки О с угловой скоростью ш (рис. 26). Пусть г есть радиус-вектор точки Р относительно точки О. Тогда скорость точки Р, равная величине ©-ОР-зшв, перпендикулярна плоскости PON и, следовательно, скорость есть вектор © X г.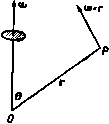

Рис. 26.

О г р

Рис. 27.

Аналогично вектор момента силы F, приложенной к точке Р, относительно точки О равен rxF (рис. 27).

Так как величина aft sin 0 равна площади параллелограмма, построенного на векторах а и Ь, то векторное произведение а X b можно рассматривать как направленную меру этой площади, т. е. вектор, величина которого равна этой площади и который направлен перпендикулярно к ней.

2.121. Закон днстрибутнвностн. Как скалярное, так и векторное произведения дистрибутивны, т. е.

a(b-fc)= аЬ-Ьас

ах (b + c) = axb--axc.

Доказательство этих соотношений представляем читателю (см. примеры 27, 28 к гл. 2).

2.13. Тройное скалярное произведение. Если а, Ь, с -три вектора, то комбинация а(Ьхс) называется их тройным скалярным произведением. Это есть скалярное произведение векторов а и Ьхс. Тройное скалярное произведение равно объему параллелепипеда, построенного на векторах а, b и с.

Доказательство. Так как вектор Ьхс равен по величине площади параллелограмма и направлен вдоль нормали к нему в ту же сторону, что и вектор а (рис. 28), то тройное скалярное произведение измеряется объемом параллелепипеда, построенного на векторах а, b и с, что и требовалось доказать.

Таким образом,

а (Ь X с) = b (с х а) = с X (а X Ь). Но (Ь X с) - а (с X Ь), так как

Ьхс = -схЬ.

Заметим, однако, что

a(bxc) = (bxc)a.

Следовательно, имеет место правило цикличности: тройное скалярное про-измдение изменяет знак только при изменении циклического порядка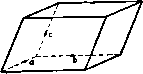

Рис. 28.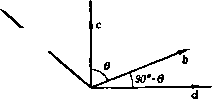

перемножаемых векторов. Заметим также, что действительное положение знака X несущественно, так как

(а X Ь) с = а (Ь X с) = [аЬс].

Последнее выражение справа является удобным обозначением тройного скалярного произведения.

Если два вектора равны или параллельны или если все три вектора компланарны то тройное скалярное произведение равно нулю, т. е.

1ааЬ] = 0. (1)

2.14. Тройное векторное пронзведение. Если а, Ь, с -три вектора, то комбинация ах(Ьхс) называется тройным векторным произведением.

Это есть векторное произведение векторов а и b х с. Заметим, что а X (Ь X с) = - а X (с X Ь) = (с X Ь) X а. Отсюда следует правило центрич-

ности: знак тройного векторного произведения изменяется только с изменением центрального вектора. акГ1кс)Ч Тройное векторное произведение

обладает очень важным свойством, ко-

торое выражается соотношением

а X (Ь X с) = - (аЬ) с + (ас) Ь.

Рис. 29. Доказательство. Вектор

а X (Ь X с) перпендикулярен вектору (Ь X с), который в свою очередь перпендикулярен плоскости, содержащей векторы b и с. Таким образом, вектор а х (Ь х с) лежит в плоскости векторов b и с и, следовательно, может быть выражен через векторы b и с соотношением

ахфхс) = рЪ-дс,

где р и - скаляры. Так как вектор ах(Ьхс) перпендикулярен а, то скалярное произведение этих двух векторов равно нулю. Следовательно,

0 = раЬ-ас.

Таким образом,

р = Яас; q = Я,аЬ,

где А. -скаляр. Отсюда следует, что

а X (Ь X с) = - Я (аЬ) с -Ь Я, (ас) Ь.

Чтобы определить скаляр X, составим скалярное произведение с некоторым вектором d, который компланарен векторам b и с и перпендикулярен вектору с (рис. 29). Тогда cd = 0 и, следовательно,

A.bd(ac)-d[ax (Ь X с)] = а [(b хс) х d].

Здесь мы использовали свойство тройного скалярного произведения. Далее, вектор (Ь X с) X d компланарен векторам b и с и перпендикулярен вектору d; следовательно, он параллелен вектору с. Если 6 -угол между векторами b и с, то величина этого вектора равна

bed sin 0 = W cos (90* - в) с

и поэтому имеет место равенство

(Ь X с) X d = (bd) с.

) То есть лежат в одной плоскости.- Прим. ред.

Отсюда находим, что

Я, (bd) (ас) = (ас) (bd)

и, следовательно, Я=1, что и требовалось доказать. Заметим также, что равенство

(а X Ь) X с = -а (be) + b (ас)

можно получить с помощью мнемонического правила: член с отрицательным знаком всегда получается сдвигом скобок в тройном произведении при сохранении порядка сомножителей.

2.15. Разложение вектора. Если а, Ь, с - заданные некомпланарные векторы, а х -произвольный вектор, то

x[a(bxc)J = a((bxc)x]-f b[(cxa)xj-f с((ах Ь)х], (1)

X [а (Ь X с)] = (Ь X с) (ах) + (с х а) (Ьх) -f (а х Ь) (сх). (2)

Первое выражение есть разложение х вдоль данных векторов, а второе - разложение х по направлениям, перпендикулярным плоскостям be, са и аЬ.

Доказательство равенства (1). Так как векторы а, Ь, и с некомпланарны, то мы можем разложить вектор х по этим векторам и получить соотношение

x = pa-b9b-f/1С,

где р, <7 и г-скаляры. Умножим это равенство скалярно на вектор (Ьхс), перпендикулярный b и с, тогда получим равенство

x(bxc) = pa(bxc) 1),

которое определяет скаляр р.

Доказательство равенства (2). Пусть

X = р (Ь X с) -f 9 (с X а) -f г (а X Ь).

Умножим это равенство на вектор а, перпендикулярный с х а и а х Ь. Тогда получим соотношение

ах = р[а(Ьхс)1

и отсюда найдем скаляр р.

2.16. Индефинитное, или диадное, произведение*). Для данных двух векторов а и b в дополнение к скалярному и векторному произведению введем индефинитное, или диадное, произведение этих векторов

Это произведение, которое мы назовем диадой, не имеет геометрической интерпретации. Оно представляет собой некоторый оператор, очень полезный при преобразовании векторных выражений.

Тензором второго ранга называется сумма диад

(а; b)-f(c; d)-f (е; f).

Скобки в этом выражении можно опустить.

Определим скалярное произведение некоторого вектора с и диады а; b следующим образом:

(а; b)c = a(bc); с(а; b) = (ca)b.

>) Аналогично определим q и г. Полученные выражения затем подставим в равенство 1 (Ь ж c)l = lpa-f(;b-frc][a (Ьхс)].-Ярил. ред.

*) Более подробно об этом см. приложение к гл. 2.-Прим. ред.

Таким образом, скалярное произведение диады и вектора является вектором, причем этот вектор зависит от того, где стоит вектор с: слева или справа от диады.

В качестве примера скалярного произведения диады и вектора можно привести тройное векторное произведение

ах(Ьхс)= -(ab)c + (ac)b = al-(b; с) + (с; Ь)1,

которое, кроме того, иллюстрирует свойство дистрибутивности определенного выше произведения.

Единичной диадой I, или идемфактором, называется такой тензор, что для любого вектора а имеют место равенства

/а=а/ = а. (1)

Мы докажем существование единичной диады при помощи следующего выражения для нее:

/ = i; i+j; j+k; к. (2)

где i, j, к -взаимно пегтендикулярные единичные векторы. На основании разложения (см. п. 2.15) мы можем записать соотношение

а = Oil + oij -Ь Озк,

и непосредственным составлением соответствующих произведений диад и векторов легко доказать справедливость равенств (1). Рассмотрим тензор

Ф = а; Ь+с; d-be; f. (3)

Фе = Ь; a+d; c-f-f; е, (4)

полученный перестановкой сомножителей в каждой диаде, называется сопряженным тензору Ф.

Если г -некоторый вектор, то

Фг = a(bг) + c(dr)Ч-e(fг)=гФe. (5)

Если Ф=Фс, то говорят, что тензор Ф симметричный, и тогда

Фг = гфд = гф.

Если Ф= - Фс. говорят, что тензор ф антисимметричный, или косой. Если Ф -произвольный тензор, то можно записать

Ф=4-(Ф + Фс) +4-(Ф-Фс)- (6)

Тензор V (Ф + Фс) симметричный, так как

(Ф-Ь Фс) г = гФс-ЫФ = г (Ф Ч-Фс).

Аналогично доказывается, что тензор V2 (Ф -Фс) является антисимметричным тензором. Таким образом, произвольный тензор может быть представлен (причем единственным образом) суммой симметричного и антисимметричного тензоров.

Если в выражении (3) заменить диадное умножение скалярным, то получим скаляр, который называют первым скалярным инвариантом тензора Ф и записывают в виде

Ф^ = ab-Ьcd-l-ef. (7)

Скалярное произведение двух диад (а; Ь) и (с; d) определяется равенствами (а: Ь) (с; d) = а (be); d = а; (be); d = (be) (a; d) = (a; d) (be) (8)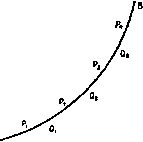

И снова представляет собой диаду. Произведение диад не меняется при переносе скаляра (be).

Из дистрибутивности скалярного произведения диад следует, что скалярное произведение дву.х тензоров второго ранга есть снова тензор второго ранга.

Если мы возьмем первый скалярный инвариант от правой части равенства (8), то получим скаляр, который называется двойным скалярным произведением диад и означает следующее:

(а; Ь) (с; d) = (ad) (be) = (cb) (da) = (с; d) (a; b). (9)

Отсюда видно, что двойное скалярное произведение диад коммутативно.

Из дистрибутивности этого произведения выводится двойное скалярное произведение двух тензоров Ф и У:

Ф..Ч'=Ч'..Ф = Фе..Ч'е = Ч'е..Фс. (Ю)

Отсюда следует, что скалярное произведение тензоров не меняется, если оба тензора заменить на их сопряженные тензоры.

Так, если S - симметричный, а Л - антисимметричный тензоры второго ранга, то

S..A = S,..Ac=-S..{-A)= -S..A.

Следовательно, S.. Л = О, т. е. двойное скалярное произведение симметричного и антисимметричного тензоров равно нулю.

2.19. Скалярные и векторные поля. Если каждой точке пространства поставлен в соответствие скаляр, то говорят, что определено скалярное поле. Так, например, давление жидкости р и плотность жидкости q образуют скалярные поля.

Если каждой точке пространства поставлены в соответствие скаляр и некоторое направление, т. е. каждой точке поставлен в соответствие вектор, то говорят, что определено векторное поле. Одним из наиболее важных векторных полей в гидродинамике является поле вектора скорости ц. Другим важным полем является поле внхря (см. п. 2.41).

2.20. Криволинейные, поверхностные и объемные интегралы. В этом пункте вводятся понятия криволинейного, поверхностного и объемного интегралов, поскольку впоследствии мы будем использовать эти термины. Здесь не будут излагаться методы вычисления таких интегралов или условия, при которых они существуют, так как эти вопросы освещены в курсах математического анализа. Однако в отдельных случаях при решении примеров нам придется делать численные оценки интегралов.

Пусть АВ - некоторая дуга заданной кривой (не обязательно плоской). Точками Qi, Q2. 1 разобьем дугу А В на N частей AQi,

<?1<?1.....Qs-iB, длины 6si, 6s2.....бs, каждая

из которых меньше е, и возьмем точки Pj, Рг,...

.. Рл-по одной на каждой части разбиения. На рис. 30 показан случай разбиения при N 4. Рис. 30.

Пусть /(Р), или для краткости просто f, есть функция, значение которой известно в каждой точке Р кривой АВ, и пусть функция / в точках Ри Рг, ..., Ру принимает значения /2, .... fn. Тогда мы можем составить сумму

/,6s, + /гбзг 4- ... + /бsv = 2/6s. (1)

Если ЧИСЛО N неограниченно возрастает и в то же времй е стремится к нулю, то линейный интеграл от функции / вдоль прямой АВ или криволинейный интеграл от / вдоль кривой АВ определяется равенством

[ /ds = lim 2/6s.

. J . iV-.oe>

Это определение справедливо независимо от того, является ли функция / вектором или скаляром.

Если функция / - вектор, то сумма в формуле (1) представляет собой векторную сумму, которая может быть получена по закону сложения векторов, и интеграл тогда является векторной величиной.

Если функция / - константа, т. е. / имеет одно н то же значение с в каждой точке дуги АВ, то из формулы (1) видно, что сумма равна с/, где /-длина дуги АВ. В этом случае величина интеграла равна с1.

Если функция / является скаляром и удовлетворяет неравенству

M>f>m, (2)

где М и т-фиксированные числа, то ясно, что выполняются следующие неравенства:

2(Л1-/)б5>0, 2(/-m)6s>o.

и. следовательно,

ZAf6s>2/6s>2m6s, откуда получим соотношение

М1> fds>ml.

Пусть i, - единичный вектор, направленный по касательной к элементу дуги ds. Тогда определим вектор ds равенством ds=:itds. Вектор ds представляет собой направленный элемент дуги кривой АВ; теперь мы можем записать тождество

J Xds= 5 Xl.ds.

(Л В) (АВ)

Таким образом, интеграл слева определен через известный уже интеграл. Здесь X может быть скаляром или вектором, а произведение под зна-Р и с. 31а. ком интеграла может быть скалярным, вектор-

ным или диадным. Чтобы определить поверхностный интеграл от функции f = f(P) по поверхности 5 (не обязательно плоской или замкнутой), разобьем поверхность на элементы, у которых площади равны 6St, 6S 6S3, .... 6Sn, а наибольшие линейные размеры не превосходят в (рис. 31а).

Если обозначить значения функции / в точках Pj, Р .., Ру, взятых иа элементарных площадках, через /1, ft, .... /iv, то мы можем образовать сумму

/i6S. + /,6S, + ... + hbSy = 2 f6S. Тогда интеграл от функции / по поверхности S определяется равенством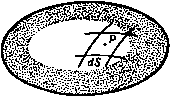

/ dS = lim 2/6S.