Это определение справедливо и для скалярных и для векторных функций.

Если функция / имеет постоянную величину с на поверхности S, то поверхностный интеграл равен сА, где Л -площадь поверхности S. Кроме того, если функция / удовлетворяет неравенству (2), то

МА>[ fdS>mA.

Если п -единичный вектор, направленный вдоль внешней нормали к элементу dS замкнутой поверхности S, то

ndS = 0,

так как легко заметить, что проекция этого вектора на любую фиксированную плоскость равна нулю.

Часто бывает удобно заменить произведение ndS вектором dS, который представляет собой элемент площади поверхности, направленный вдоль нормали к ней (ср. п. 2.12). При помощи этого обозначения соотношение (3) принимает вид

dS = 0.

В общем случае мы приходим к рассмотрению интегралов типа

\ XdS,

Рис. 316.

где X может быть скаляром или вектором, а умножение скалярным, векторным или диадным.

Чтобы определить интеграл по объему, рассмотрим объем V, заключенный внутри замкнутой поверхности S (рис. 31 б). Разобъем этот объем

на элементарные объемы бТ), бтг, бТз.....бтлг, у которых максимальные

линейные размеры не превосходят 8. Если обозначить значения функции / в точках Pj, Рг, Рз. P/V. взятых внутри элементарных объемов, через fu fiufi . fs, то можно составить сумму

/i6ti + /гбТа + Ьбхз +...+ убт^ = 2 /бт.

Тогда интеграл от функции / по объему V определяется следующим образом:

[ /dT = lim2/6T.

Af-.oo

<V) е-о

Это определение снова применимо и к векторным и к скалярным функциям.

Если функция / имеет постоянную величину с, то интеграл равен cV, а если / удовлетворяет неравенству (2), то справедливо соотношение

MV> { fdx>mV.

Замечание. Мы пишем один знак интеграла, когда используем только один дифференциал ds, dS или dr. Если мы используем два дифференциала, то будем писать два знака интеграла. Так, если dS - dxdy, запишем

\ fdS=\fdxdy.

(S) (S\

Фо-Фя=ясг(-). (I)

где через {df)/ds)pQ обозначена скорость изме-Р и с. 32. нения функции ф при смещении точки в на-

правлении PQ.

Пусть /?-произвольная точка, близкая к Р, и пусть поверхность уровня ф = фл пересекает отрезок PQ в точке S. Примем, что с точностью до малых первого порядка отрезок RS перпендикулярен отрезку PQ. Тогда

так что

Фя - Фр = PR cos в PR (grad ф), (2)

где через gгadф обозначен вектор), направленный вдоль PQ и равный по величине

Из ЭТОГО определения после замены вектора PQ на ndn, где п -единичный вектор, направленный вдоль нормали к поверхности уровня функции в точке Р, следует равенство

grad ф =-II-п. (3)

Для gradф применяются различные обозначения:

g dФ==4-=Vф=n. (4)

в первом из них изменение координаты радиуса-вектора точки Р обозначено через dr, а во втором изменение координаты радиуса-вектора обозначено через dP. Преимущество последнего состоит в том, что обозначение явно указывает на точку Р. (>5означение дц>/дт можно сравнить с обычной частной производной д<р1дх, но следует помнить, что мы не можем делить на вектор, так что выражение Лр/дг нельзя рассматривать как предел отношения двух малых величин. Символ V (произносится набла ) введен Гамильтоном и называется так потому, что знак V формой напоминает арфу *). Векторный оператор? аналогичен скалярному оператору D - d/dxTew, что это обозначение не указывает явно независимую переменную. Тем не менее это обозначение удобно. В дальнейшем мы будем использовать то обозначение из равенств (4), которое окажется более подходящим к рассматриваемому случаю.

Обозначение gradip является сокращением фразы градиент функции ф . *) По-гречески vaXa-арфа. -Прим. перев.

2.22. Изменение скалярной функции координат. Пусть ф -скалярная функция точки в пространстве, так что значения функции ф образуют скалярное поле. Будем предполагать, что функция ф непрерывна вместе со своими первыми частными производными. Тогда существует, вообще говоря, семейство поверхностей, на каждой из которых функция ф постоянна. Мы назовем их поверхностями уровня функции ф.

Пусть Р - произвольная точка, а Q -близкая к ней точка, лежащая на нормали к поверхности уровня ф = фр в точке-Я (рис. 32). Через фя обозначено значение функции ф в Р. Тогда если рассматривать PQ как величину первого порядка малости, то можно

записать

Возвращаясь к равенству (2), отметим, что скорость изменения функции ф при перемещении точки по направлению PR равна

и является компонентой вектора gradф по направлению PR. Таким образом, если в равенство (2) ввести обозначение

PR = i,ds,

то мы получим соотношение

= i.grad9=i.-i,(V9).

Следовательно, мы должны рассматривать V как векторный оператор, применение которого к скалярной функции <р дает вектор, компонента которого по любому направлению равна скорости изменения функции ф по этому направлению.

2.23. Другое выражение для градиента функции. Рассмотрим цилиндр S, ограниченный поверхностями уровня ф = фр и ф=фо, причем точка Q находится на нормали к поверхности ф = фр в точке Р (рис. 33). Пусть PQ - бесконечно малая величина первого порядка, пусть диаметр нашего цилиндра считается малым по сравнению с PQ, а образующая цилиндра перпендикулярна поверхности

ф = фр-

Введем единичный вектор внешней нормали к элементу dS поверхности цилиндра п и рассмотрим выражение

\ ntpdS.

Рис. 33.

Так как диаметр поперечного сечения цилиндра-бесконечно малая второго порядка, то

функцию ф можно считать постоянной на линии, ограничивающей нормальное сечение цилиндра. Следовательно, интеграл (1) боковой поверхности цилиндра равен нулю [ср. с формулой (3) п. 2.20]. Если через ю обозначить площадь поперечного сечения цилиндра, то интеграл (1) приближенно можно представить следующим образом:

J ПфЙ5=П<фоС0-Ь Прфр(0 = (0 [пд{фр-}-Р<?(4)рд}+Рр = (S)

= bnPQ (grad ф) = V (grad ф), где V - объем цилиндра. При этом мы использовали равенство

Пр-ЬПо = 0.

Заменим теперь цилиндр произвольной малой выпуклой поверхностью 5, окружающей точку Р. Тогда поверхность S можно разбить на цилиндры типа, описанного выше, и так как интегралы по внутренним границам пропадают, то получается приближенное равенство

jj nфdS=K(gradф),

аГ = Ж = Ч' = агас1ф=Ит f \ Пфй5. (3)

?Ф=Ит- nфdS = gradф, (2)

VF = lim -р- nF dS = div F ), (3)

VxF = lim-i-? nXFds = rotF,. (4)

V;F=lim-i-C n; FdS. (5)

В формулах (2) -(4) справа даются обозначения соответствующих понятий.

Из формулы (2) следует (ср. п. 2.23), что данное здесь определение оператора V не противоречит первоначальному определению V как оператора градиента над скаляром.

Отметим также, что V является векторным оператором в том смысле, что если п есть некоторый вектор, то выражения пф, nF или п X F

1) div F читается сдивергенция F . Векторное поле, в каждой точке которого дивергенция равна нулю, называется соленоидальным, а векторное поле, в котором вихрь равен нулю, называется безвихревым.

где К -объем, ограниченный поверхностью S. Следовательно, с принятой нами точностью

gгadф = -p- { tvfdS.

Таким образом, если 5 -произвольная поверхность, окружающая точку Я, то мы можем записать соотношение

где К -> О означает, что поверхность S стягивается в точку таким образом, что она всегда окружает точку Р, когда наибольший линейный размер поверхности стремится к нулю.

2.24. Обобщенное определение оператора V. Мы видели, что в результате применения векторного оператора V к скалярной функции ф получается вектор gгadф, определяемый формулой (3) п. 2.23. Это обстоятельство, естественно, побуждает нас выяснить смысл выражений VF, V X F, V; F, где F -некоторая векторная функция, зависящая от координат. В последующих рассуждениях будем считать X некоторой функцией координат; эта функция может быть как скалярной, так и векторной. Тогда определим оператор VX равенством

VX=lm-ir{ nXdS, (1)

где V-объем, ограниченный поверхностью S; точка Р, в которой вычисляется величина VX, является внутренней по отношению к поверхности S, когда максимальный линейный размер S стремится к нулю. Через п обозначен единичный вектор внешней нормали к элементу поверхности dS. В выражении VA умножение может быть скалярным, векторным или диадным, если X является вектором. Подставляя вместо X сначала скаляр ф, а затем вектор F, мы получаем следующие определения:

\т1[ащй5=а lim- nfdS] =a(V(p) = (aV)(p, (1)

V-.0 Lvo J

lim-i-C (an)FdS = a lim С (n; F)dS =a(V; F) = (aV)F. (2)

(S, (S)

Если положить a = ai, то из формулы (5) п. 2.22 видно, что выражение (aV)(p равно вектору а, умноженному на скорость изменения функции ф по направлению вектора а.

Отметим, что (aV) -скалярный дифференциальный оператор. Чтобы выяснить геометрический смысл соотношения (2), заметим, что вектор F имеет некоторые скалярные компоненты вдоль трех произвольных фиксированных некомпланарных векторов и, следовательно, выражение (aV)F равно произведению величины а на скорость изменения вектора F по направлению вектора а. Кроме того, так как (aV) является скалярным оператором, то обычные правила дифференцирования произведения дают нам соотношения

(а?) (bc) = bI(aV)cH-cI(aV)bl, (3)

(а?) (bxc)=((aV)b]xc + bx((aV)cl. (4)

Заметим также, что для бесконечно малого приращения радиуса-вектора точки имеют место равенства

dip={drV)(f = driV<f),

dq=(drV)q.

В качестве приложения рассмотрим следующий важный пример. Пусть скорость жидкости в точке Р равна q, а скорость жидкости в точке Q, положение которой относительно Р определяется бесконечно малым вектором ц, равна q (рис. 34). Тогда с точностью до членов первого порядка малости можно записать соотношение

q = q + (4V)q.

2.32. Некоторые дифференциальные операции над одним вектором или скаляром. Если (р является скаляром, то

div (gradф) = V (?(р) = (VV) ф = VV (I)

остаются соответственно вектором, скаляром или вектором, если п заменяется на V.

Таким образом, из соотношения (1) и из формул

а(пф) = (ап)(р, а(п; F) = (an)F

следуют равенства

a(Vf) = (aV)f, a(V; F) = (aV)F. (6)

В общем случае мы можем обращаться с формулами, которые содержат оператор V, так как если бы V был обычным вектором; при этом необходимо иметь в виду, что в полученном результате оператор V не может быть крайним правым множителем и что мы различаем переменные векторы и векторы постоянные.

2.31. Оператор (aV). Пусть а -некоторый вектор, не изменяющийся при переходе к пределу в формуле (1) п. 2.24. Тогда, применяя правила п. 2.16 и учитывая, что V -векторный оператор, получаем соотношения

V X (V X а) = lim lim И nj х (iig х а) dSj dS, =

Vl- 0 V- 0 12 J J

= lim lim-r Ц [n8(n,a)-(n,n0a]dSadS, = v;(Va)-Va.

V.->0 V -0 IZ J J

Эти примеры доказательств показывают, что правила обращения с оператором V в конечном счете основываются на соответствующих правилах обращения с вектором п.

2.33. Некоторые операции над произведением величин. Чтобы изучить операции над произведением XY, предположим, что при умножении X \\ Y подчиняются следующему закону:

(X -hX) (У -hУ) = ХУ + XY + Х'У + XT,

где порядок сомно.жителей в каждом из произведении, вообще говоря, существен.

Пусть через X и У обозначены величины функций в точке Р, а через X и У' -их величины в точке на замкнутой поверхности S, окружающей

Оператор V* называется оператором Лапласа.

Из формулы (1) п. 2.13 следует соотношение

div(rota) = V(Vxa) = IVVal=0. (П)

Учитывая результаты п. 2.12, легко получить равенство аха = 0 и, используя его, вывести соотношение

rot (grad ф) = V X (?ф) = (V X V) ф = 0. (III)

Очевидно, что имеет место тождество

rot(rota) = Vx(Vxa). (IV)

Используя свойства тройного векторного произведения, получаем формулу

rot (rot а) = V (Va) - (VV) а = grad (div a) - V*a.

Таким образом,

V*a = V(Va)-Vx(Vxa). (V)

Все эти соотношения можно доказать непосредственной проверкой. Например, для доказательства равенства (II) запишем, используя обычные обозначения:

V, (Va X а) = lim lim -5717- ni (Пг X а) dS dSi =

Vi->0 Уг->0 t2 J J

= - lim lim хпт- \ (ni X a) dSj dS. Уг- о Vi- o J

При этом мы использовали правило цикличности в тройном скалярном произведении и предположили, что порядок интегрирования может быть изменен. Таким образом,

Vi(V*Xa)= -V2(ViXa),

или

V(Vxa)= - V(Vxa) = 0. Аналогичным образом доказывается равенство (V):

точку Р. Через п обозначим вектор единичной нормали к элементу поверхности dS. Тогда можно записать тождества

XY\X + {X-X)] iY + {Y-Y)] =

- XY+X (Y-Y) + iX-X) Y + {X-X) {Y - Y),

R, следовательно,

\ nXYdS= nXYdS+ nX{Y-Y)dS +

+ niX-X)YdS+\ n(X-X) (y-Y)dS.

Если теперь мы будем стягивать в точку поверхность, окружающую точку Р, то величины Х'-Х и К' -У станут бесконечно малыми и, следовательно, последний интеграл станет бесконечно малой величиной по сравнению с остальными интегралами, поэтому им можно будет пренебречь.

Кроме того, значения функций X и У в точке Р фиксированы,

а ndS = 0, если поверхность замкнутая (см. формулу (3) п. 2.20]. Отсюда

следует

5nXydS=0; (1)

учитывая это равенство, мы получаем соотношение

nXTdS=5 nX{Y-Y)dS+ J n{X-X)YdS =

s s s

= J nXY dS-b J nXYdS. s s

Разделив обе части последнего равенства на величину объема V, ограниченного поверхностью S, преобразуем это равенство к виду

-i- I nXYdS = -nXYdS + -L J nXYdS.

Если теперь совершим предельный переход V-0, то, учитывая определение оператора V, получим равенство V (XY) = V (XcY)+V (XY), где индекс нуль указывает, что соответствующая величина под знаком оператора V считается постоянной*). Эту формулу можно сравнить с соответствующей формулой для дифференциального оператора D=dldx, а именно

D (XY) = D (Х„К) + D (ХКо) = X, (DY) + (DX) К„ = X (DK) + (DX) Y.

В атом соотношении индекс нуль опускается, когда он больше не требуется. Последнее свойство вместе со свойством градиента (см. п. 2.23) показывает, что V является обобщенным дифференциальным оператором.

2.34. Применение оператора V к некоторым произведениям. Теперь применим результаты предыдущего пункта к некоторым произведениям

) Заметим, что этот переход носит существенно предварительный характер при нахождении результата действия оператора V на произведение [ср. формулы (11), (III) II. 2.34].

векторов и скаляров, имея в виду, что оператор V никогда не может быть крайним правым множителем в произведении. Для тройного скалярного и тройного векторного произведений можно получить следующие формулы, которые мы будем использовать в дальнейшем:

p(qxr) = r(pxq)=-q(pxr), (А)

px(qxr) = (rp)q-r(pq), (В)

p(qr) = qx(pxr)-l-(qp)r. (С)

Очевидно, что формула (С) получится из формулы (В) простой перестановкой сомножителей.

Из формулы (А) следует равенство

V (а X Ь) =V (а X bo) +V (зо х b) =

= bo(Vxa)-ao(Vxb). (I)

Теперь нулевой индекс можно отбросить и тогда получим соотношение V(axb) = b(VXa)-a(Vxb),

div (а х b) = b rot а - а rot b. Из формулы (В) следует равенство

V X (а X Ь) = V X (а X bo)--V X (ао X Ь) =

= (boV)a-bo(Va)-(aoV)b-fao(Vb), (II)

или

V X (а X Ь) = (bV) а - (а?) b - b (Va)-Ь а (Vb). Из формулы (С) следует равенство

V (аЬ) = V (аоЬ) + V (аЬо) = а X (V х Ь) -Ь (aV) b +

-bbx(Vxa) + (bV)a. (Ш)

Из равенств (II) и (III) вычитанием получаем следующую формулу: (aV) b= у (V (ab)- V X (а х b)-b х (V X а) -а х (V X b) -

-b(Va)4-a(Vb)l. (IV)

В частности, так как V х (q X q) = О, то имеет место равенство

(qV)q = yVq -qX(Vxq).

Вели величина t)-постоянный вектор (который не подвергается действию ператора V), то из равенств (II) и (III) следуют соотношения

(4V)b=-Vx(4Xb) + n(Vb),

(tlV)b = V(tib) + (Vxb)xi].

Если величина ф -скаляр, то получим равенство

V (аф) = V (фоа) + V (фао) = Ф (Va) --а (Vф), (VI)

или

div (фа) = ф div а + а grad ф.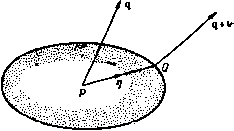

*) Действительно, это центральная поверхность типа эллипсоида, так как если ц принадлежит поверхности, то и -1\ принадлежит ей.

Если ф и г(5 -скалярные функции, то имеет место равенство V X (аф) = V X (аоФ) f V X (афо) =

=-ах?ф + ф{?ха), (VII)

или

rot (аф) = ф rot а - а X grad ф,

а также равенство

V (фг)) = V (фог|з) +V (фгЗо) = ф?гЦ- г|з?ф. (VIII)

Используя равенство (VIII), а затем равенство (VI), получаем следующую формулу:

V (ф1) = 7(Vфгз) =

= pV\ + 2 (?ф) (Vt) -f ф?8г|). (IX)

Кроме того, справедливо следующее равенство: V(a; b) = V(a; bo)-fV(ao; b) =

= b(Va)-b(aV)b, (X>

которое в частном случае приводится к виду

V(q; q) = q(Vq)+(qV)q.

2.40. Анализ движения элемента жидкости. Рассмотрим бесконечно малый элемент жидкости с центром в точке Р.

Пусть радиус-вектор точки Q этого элемента жидкости относительно точки Р равен ц (рис. 35). Тогда, если скорость жидкости в точке Р равна q, скорость в точке Q, согласно п. 2.31, будет равна

q + v = q-f (4V)q. (1)

Рассмотрим уравнение

[(tjV) q]i\ = c,

где с -некоторая постоянная. Левая часть этого уравнения является однородной квадратичной функцией относительно компонент вектора i\ и,

следовательно, представляет собой Рис.

поверхность второго порядка*). Найдем нормаль к поверхности в точке с радиусом-вектором г\. Если вектор dr\ лежит в касательной плоскости к поверхности в точке Q, то вектор ц di\ с точностью до малых первого порядка относительно величины di\ удовлетворяет уравнению поверхности. Поэтому после подстановки tj-j-dij в уравнение поверхности и отбрасывания члена второго порядка, содержащего величину dt) dr\, мы получим уравнение

l(4V)qld4 + [(d4V)ql4 = 0- (2)

Но так как оператор V действует -на вектор q и не действует на вектор г\, то из формулы (3) п. 2.31 мы находим соотношение

[(dV) q] Л - (dnV) Ш = dn \V (qn)].

Из равенства (V) п. 2.34 следует соотношение

V (ял) = - (V X q) X + Ш q.

Следовательно, из формулы (2) получаем уравнение

1Ш q - (V X q) X л + Ш qJ dr\ = 0.

Так как нормаль к поверхности в точке Q перпендикулярна вектору dr\, то, следовательно, она направлена вдоль вектора

2(nV)q-(Vxq)X4 = 2/(4). (3)

Таким образом, из формул (1) и (3) мы получаем выражение для скорости жидкости в точке Q в виде

q + v = q-t-(Vxq)X44 /(П)-

Отсюда видно, что скорость в точке Q имеет три слагаемых:

1) скорость q точки Р, которая соответствует перемещеншо элемента как целого;

2) скорость V2 (V X q) х г\, которая представляет собой скорость вращения элемента как целого с угловой скоростью V2 (V X q) (см. п. 2.12);

3) скорость / (т|) относительно точки Р, направленная по нормали к той поверхности из семейства центральных поверхностей второго порядка [(nV)qlti = const, на которой лежит точка Q.

Первые два слагаемых описывают движение твердого тела; они сохранились бы. если бы элемент жидкости отвердел . Третье слагаемое, называемое чистой деформацией, может существовать только в деформируемой среде, например в жидкости. Этот тип относительного движения характерен для любой деформируемой среды, независимо от того, является ли она жидкостью или нет.

Чтобы выяснить природу чистой деформации, заметим, что центральная поверхность второго порядка имеет три взаимно перпендикулярные оси симметрии, которые нормальны касательным плоскостям к поверхности в точках пересечения ее с осями симметрии. Отрезки прямых, параллельных этим осям, растягиваются с постоянными (хотя, вообще говоря, разными) скоростями. Такое движение будет деформировать элемент, имевший первоначально форму сферы, в эллипсоид. Кроме того, заметим, что линии, взятые в направлении осей симметрии в момент времени t, останутся взаимно перпендикулярными в момент / Ь б^. Так как оси симметрии параллельны нормалям к поверхности в точках пересечения ее с осями симметрии, направление этих осей задается уравнением

ПХ/(п) = 0.

Проведенный анализ показывает, что такое описание движения связано с существенными свойствами жидкости и не зависит от выбранной системы ксюрдинат.

2.41. Вихрь. Вектор Vxq = rotq = g называется вектором вихря, или .1 росте вихрем. Угловая скорость бесконечно малого элемента жидкости, которую часто, но не совсем удачно называют молекулярным вращением, равна половине вихря. Если бы сферический элемент жидкости внезапно отвердел и одновременно исчезла бы окружающая жидкость, отвердевший элемент жидкости вращался бы с этой угловой скоростью (см. пример 13 к гл. И).

Вихревой линией называется такая линия в жидкости, касательная в каждой точке которой направлена вдоль вектора вихря в этой точке.