Это уравнение имеет очевидное решение

/(9)= -9n,axSin(/59-f е),

где е - произвольная постоянная. Так как с* = Л^тах. то отсюда

9f = 9maxSin(*9-i-e), ge = c*cos(kQ+E). (4)

Будем измерять угол 9 от начальной линии Маха то- Тогда при 9 = 0 получаем

(7mai sin е = Vo cos Ро, с* cos E=Vo sin po.

так что

\ge = kcigiio = kVfAl-l, (5)

где Mo -число Маха набегающего потока, имеющего скорость Vo- Найдем положение линии Маха mi. На этой линии имеем 0 = 9, = роЧ-а -Рч. где а -угол, который прямая ВС образуете АВ, т. е. угол, на который поворачивается набегающий поток. Тогда

V,cosn, = £7maiSin(*e,--e), yjSinn, = c*cos(*ei--e). (6)

Деля эти уравнения одно на другое, получаем формулу для р,; величина Vi определяется, далее, из равенств (6). Для определения давления имеем

Поэтому

У^ = с^д1= с**cos (*6 + е).

/ р \ V 2COS*(fee-be) .yv

ПОЛОЖИМ, что конечное состояние газа представляет собой равномерный поток со скоростью Vi, параллельной стенке ВС. Тогда поворот будет полностью завершен на второй прямой линии Маха т,. Метод характеристик сразу показывает, что все линии Маха, выходящие из точки В, будут прямыми и что на любой из этих линий Маха (скажем, т) скорость в каждой точке будет одна и та же. Если ф - потенциал скоростей, то отсюда следует, что составляющие скорости

= -f. e=-t (1)

не зависят от г. Кроме того, поскольку т является характеристикой, то qe = c и, следовательно, уравнение Бернулли (4) п. 1.63 дает

(liy-=-<V-)[vU-(ty-(7l)]-

Поскольку Qr и 9в не зависят от г, то попытаемся удовлетворить уравнениям (1) и (2), полагая

Ф = г/(е), (3)

где / (9) не зависит от г. Тогда, подставляя функцию (3) в уравнение (2), получаем с помощью формулы (4) п. 20.42 следующий результат:

(/(9)1+[/(9)1 = 9шах.

Физически возможное максимальное значение 9 соответствует нулевому значению давления (р=0), т. е.

Следовательно, если а+ ц.о > 9

mail Т. е. если

ТО газ не будет прилегать к стенке ВС, а будет отделен от нее областью вакуума, которая ограничена стенкой ВС и линией 9 = 9тах, одновременно являющейся линией тока и характеристикой.

Если стенка не имеет излома, а представляет собой непрерывно изогнутую кривую, то ее можно заменить приближенно ломаной линией и решение получить предельным переходом. Однако в этом случае проще пользоваться методом характеристик.

Наконец, отметим, что рассмотренное течение является безвихревым и гомэнтропическим, поэтому оно обратимо. Течение, изображенное на рис. 355, представляет собой течение разрежения, т. е. давление и плотность уменьшаются в направлении течения, а линия Маха гпо отклонена в сторону от набегающего потока. Если обратить направление движения на всех линиях тока, то характеристика mi будет отклонена в сторону набегающего потока со скоростью Vi и течение будет течением сжатия, сопровождающимся увеличением давления и плотности.

20.60. Ударные волны. Если метод решения, развитый в п. 20.50 для расчета обтекания выпуклой стенки, попытаться применить для случая вогнутой стенки, то можно обнаружить, что здесь линии Маха имеют огибающую Е (рис. 356).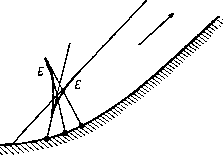

Рис. 356.

Это обстоятельство повлекло бы за собой математически неопределимое состояние течения, когда скорость газа определялась бы неединственным образом. Такое состояние физически невозможно. Экспериментальные наблюдения показывают, что в этом случае возникает ударная волна {скачок уплотнения), которая начинается в точке возврата огибающей и проходит между двумя ее ветвями. При пересечении этой линии нормальная составляющая скорости скачкообразно уменьшается ), а плотность, давление, температура

1) Ниже будет установлено, что касательная составляющая скорости при этом не изменяется; поэтому полная скорость при переходе через ударную линию всегда уменьшается.

И энтропия скачкообразно увеличиваются. На рис. 357 изображены течение со скачком уплотнения и течение разрежения, имеющие место при обтекании плоского профиля ВС.

Здесь прямая линия тока АВ подходит к профилю в точке В, а прямая линия тока CD сходит с него в точке С.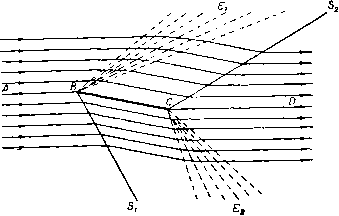

Рис. 357.

На верхней поверхности у излома ABC имеется течение разрежения Ей в котором набегающий поток разворачивается так, что становится параллельным ВС. Затем поток обтекает вогнутый излом BCD и проходит через скачок уплотнения Sz, возникающий в точке С. Аналогично на нижней поверхности имеют место скачок уплотнения Si в точке В и течение разрежения в точке С.

Рис. 358.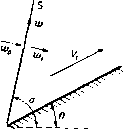

Рассмотрим прямолинейную стационарную ударную волну, которая образуется при обтекании тупого угла я - 9 (рис. 358).

Пусть индекс О относится к условиям перед скачком уплотнения S, а индекс 1 -- к условиям за этим скачком, так что Vo является скоростью набегающего потока, а Vi - скоростью потока, отклонившегося после прохода через скачок. Пусть скачок S составляет угол а с направлением скорости Vq. Обозначим через Wq и Wx составляющие скоростей Уо и Vi, перпендикулярные к S. Возьмем элемент dl скачка5 и рассмотрим условия до и после него. Согласно уравнению неразрывности, поток массы при переходе через скачок должен сохраняться, т. е.

600=611. (1)

Поскольку сила давления действует по нормали к dl, то при переходе через скачок также сохранится поток количества движения в направлении.

+ EoVl= + Ei + Vl.

Qo 2 о - е. 2 с помощью формулы (14) п. 20.01 находим

{у-1) Qo + 2 - (Y-1) ci 2 - Т

Согласно уравнению Бернулли, каждое из первых двух слагаемых в уравнении (4) равняется соответствующей величине /г^тах- Из этого следует, что tmai не изменяется при переходе через скачок.

Уравнение (4) имеет такую же форму, что и уравнение Бернулли, но состояние газа, характеризующееся параметрами (ро, Qo) и (pi, pi), соответствует здесь различным значениям энтропии. Таким образом, уравнение (4) не может быть выведено из закона для изэнтропического течения, на котором основано уравнение Бернулли. Увеличение энтропии определяется по формуле (11) п. 20.01 в виде

Из уравнений (1) и (2) следует, что касательная составляющая скорости, параллельная фронту скачка, при переходе через скачок не изменяется. Обозначив эту составляющую скорости через w, из соотношения (4) находим равенства

t = -- < Y- = - -

С помощью этих равенств заменим ро и pj в уравнении (3) и исключим далее Оо и Qi посредством соотношения (1). Тогда после простых преобразований получим следующее соотношение, принадлежащее Прандтлю:

oai = (?max-a)=C -*W. (5)

При выводе соотношения (5) использована формула (4) п. 20.42.

параллельном S. Следовательно,

QoWoVoCOsa= QiWiViCOs{a- Q). (2)

Разность сил давления на элементе скачка dl должна равняться изменению нормальной составляющей потока количества движения при переходе через dl. Следовательно,

Pi-Po = Qowl-Qiwl. (3)

Уравнения (1) -(3) представляют собой обычные законы сохранения механики. Четвертое соотношение получим, применяя закон сохранения энергии и рассматривая при этом также и тепловую энергию.

Если -внутренняя энергия, приходящаяся на единицу массы воздуха,

то полная энергия на единицу массы будет равна E + V- Приравняем

поток энергии и работу в единицу времени, совершаемую силами давления. Тогда

РоШо - р,ш, = cii (fl + у i) - QoWo (Eo + y Отсюда с учетом уравнения (1) получим

Замечая, что aJo = Vosina и oJi = V, sin (а - в), легко преобразуем уравнения (2) -(4) к следующей системе:

(6) (7) (8)

Vf, cos a = Vi cos (о - 9), Po + eoVo sin* о = pi + eiVJ sin* (0-9), (y: + T 0 sin* a = +1sin* (a - 9).

Причем последнее из этих уравнений получено путем возведения в квадрат обеих частей равенства (6), делением их на два и вычитанием этого результата из равенства (4). Полагая

AQo = ei - qo ДРо = Pi - Ро,

после некоторых простых преобразований находим из уравнений (1) и (6) равенство

Дро tg а .

Qo tg(a-e) из уравнений (1) и (3) находим равенство

Лро = QoVl sin* а

(10)

(?o--ACo

и из уравнений (8) и (10) находим равенство

AQo 2(}o-f АСо

Из равенств (9) -(11) можно вычислить Аро, Ago и а, если заданы О, ро, до и Vo.

Из формулы (11) также следует уравнение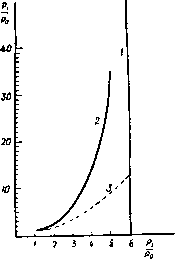

А) Qo 2

Рис. 359.

/ - асимптота; 2 - кривая Гюгонио; Я-адиабата.

которое определяет кривую Гюгонио; эта кривая, построенная в координатах pjpo и Q,/go, представляет собой равнобочную гиперболу (рис. 359). При pi/po- схэ имеем

Y+l Y-l

причем для воздуха Qi/qo 6. Таким образом, в воздушной ударной волне при максимально возможном сжатии начальная плотность воздуха возрастает только в шесть раз. На рис. 359 пунктирной кривой изображена адиабата Pi/Po = (Oi/eo)v. При Ар-О и Aq-0 уравнение (11) переходит б дифференциальное уравнение адиабаты dp/dQ=Yp/g. Кривая Гюгонио и адиабата касаются друг друга в начальной точке Oi/Qo= 1. Отношение р/д и, следовательно, температура при движении по кривой Гюгонио растут быстрее, чем при движении по адиабате.

В заключение отметим, что перед рассмотренным здесь скачком должен иметь место сверхзвуковой поток. За скачком же течение может быть как сверхзвуковым, так и дозвуковым. При переходе через скачок происходит уменьшение нормальной составляющей скорости, а касательная составляющая скорости остается при этом неизменной. Поэтому при переходе через скачок скорость отклоняется в сторону фронта скачка. Если скачок наклонен под достаточно малым углом к направлению набегающего потока, то течение за скачком может быть сверхзвуковым.

20.61. Ударная поляра. Скорость набегающего потока Vp представим в плоскости годографа отрезком OA оси и (рис. 360). Из точки О проведем также вектор ОР, представляющий собой скорость Vi потока (составляющие которой равны и, v), прошедшего через скачок и отклонившегося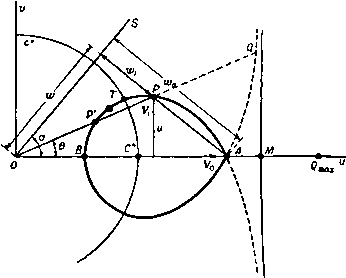

Рис. 360.

на угол 6. Геометрическое место точек Р называется ударной полярой, соответствующей скорости Уо-

В обозначениях, указанных на рис. 360, имеем

w = VoCOS.a, a o=VoSina, ©1= Fosina -,

Подставляя эти величины в уравнение (5) п. 20.60. получим VI &\v? а - УрУ tg а = k (<72iax - V\ cos а), что вместе с формулой

определяет геометрическое место точек Р {и, v), т. е. ударную поляру.

Исключение а из формул (1) и (2) непосредственно приводит к уравнению

f (<7S.ax - V\) + У„ (Уо - и)\ = (Уо - иУ (Уои - ку.). (3)

Таким образом, ударная поляра представляет собой кривую третьего порядка (декартов лист, или гипоциссоиду), симметричную относительно оси и, которую она пересекает в точках А к В (рис. 360) с координатами

М = Уо, U=fe </i ax/Vo. (4)

Тогда

ОА-ОВ = kql = с* = 0С*\

Следовательно, точки А н В связаны между собой преобразованием инверсии относительно звуковой окружности ц*-f- и* = с* . Точки на поляре, находящиеся внутри этой окружности, соответствуют дозвуковому течению

за скачком. Если

ОМ = и.

то величина v становится бесконечной и поэтому линия и = ОМ представляет собой асимптоту. Продолжим линию ОР до пересечения с ударной полярой в точке Q. Если теперь начальную скорость представить вектором 0Q, то после перехода через скачок она уменьшится до величины, которая изображается вектором OA.

Ударную поляру, соответствующую заданным значениям Уо и д^пях, можно построить точка за точкой следующим образом.

Нанесем точки А, В к М, определяемые формулами (4) и (6). Построим на линиях АВ и MB, как на диаметрах, окружности и Сг (рис. 361). Соединим точку В с какой-нибудь точкой Q на окружности Сг, и пусть линия QB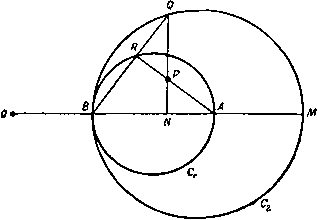

Рис. 361.

пересекает окружность Ci в точке R. Тогда точка Р, являющаяся точкой пересечения линии AR и линии QN - перпендикуляра к АВ, будет точкой ударной поляры. Доказательство этого утверждения мы предоставляем читателю в качестве упражнения.

Как пользоваться ударной полярой, видно по рис. 360. Предположим, что ударная поляра нам задана. Направление скачка, который отклоняет поток на угол О, получим, проводя нормаль к линии АР; здесь точка Р представляет собой точку, где прямая линия, проходящая через О и составляющая угол 9 с направлением набегающего потока, пересекает ударную поляру. Из этого построения получается также скорость Vi = ОР. Поскольку линия ОР пересекает ударную поляру еще в одной точке Р', то возможен еще второй скачок, направление которого перпендикулярно к АР. Однако эксперименты показывают, что для течения сжатия при обтекании излома или клина в действительности реализуется только один скачок, соответствующий точке Р. Касательная к ударной поляре ОТ, проведенная из точки О, определяет критический угол 9*, при котором два возможных скачка уплотнения совпадают. Если 9 > 9*, то проведенное выше построение становится недействительным, и в этом случае перед клином образуется отошедшая криволинейная ударная волна (рнс. 362).

Отметим, далее, что при 9 - - О, т. е. когда точка Р стремится к двойной точке А на ударной поляре, скачок становится все более слабым и условия за ним приближаются к условиям непрерывного течения без скачка. Таким

образом, в этом случае направление скачка должно стремиться к направлению линии Маха. Следовательно, угол между касательными к ударной поляре в двойной точке А должен быть равен я - 2ji, где ц - угол Маха.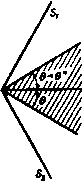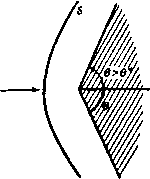

Рис. 362.

й.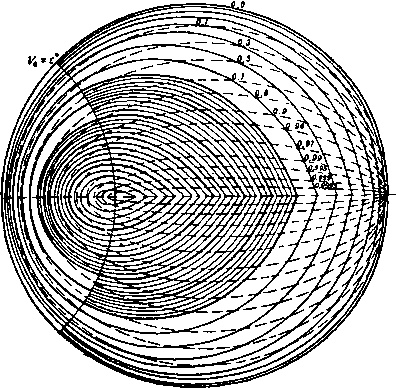

Рис. 363.

На рис. 363, принадлежащем Буземану, изображено семейство ударных поляр при с* < Vo < 9m x- Все поляры охватывают точку с* и лежат внутри окружности, к которой они приближаются при Vo <7max- Пунктиром здесь показаны кривые, иа которых постоянна величина отношения давлений торможения за скачком уплотнения и перед ним.

20.70. Характеристики в изэнтропическом течении. Установившееся течение, которое рассматривалось в п. 20.43, было гомэнтропическим. В этом пункте мы будем иметь дело с более общим случаем изэнтропического течения, в котором энтропия S остается постоянной вдоль каждой линии тока, но не обязательно * имеет одно и то же постоянное значение на разных линиях тока.

Представим себе, что поле течения покрыто геометрической сеткой, образованной некоторым семейством кривых С и семейством ортогональных кривых Л^.

Рассмотрим в некоторой точке Р кривые С и Л^. На кривой С будем обозначать через ds элемент дуги, через t - единичный касательный вектор в направлении увеличения s, через X, - кривизну в точке Р. Для ортогональной кривой соответствующие величины будем обозначать через dn, п, х„. Примем в качестве стандартного такое взаимное расположение кривых С иМ, которое показано на рис. 364 и в котором направление п получается из направления t поворотом на прямой угол против часовой стрелки.

Тогда, согласно формулам Френе ),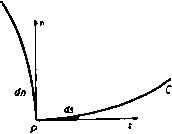

Рис. 364.

= x,n,

= - x t.

поскольку положительное направление вектора нормали к кривой (как мы условились) будет направлением -t.

Дифференцируя формулу nt = 0, получаем

п = - t = Xntt = x nn.

, дп dt

t- = -n = - x.nn = x.tt.

так как пп = 1 = tt. Следовательно,

= -x.t.

дп ds

В этих же обозначениях для вектора q=<7,t-b<7nn имеем

Если теперь применить формулу (3) к уравнениям движения (2) и неразрывности (I) п. 20.13, то с учетом формул (1) и (2) получим

да. , да. , 1 dp

+ Ж--Ж'

Q dn

0 , дц . dq.

, dq

(4) (5) (6)

Уравнение постоянства энтропии вдоль линии тока [см. (4) п. 20.13] запишется так:

-f Н'-- - Р)

)Weatherburn С. е., Elementary vector analysis, Lnd., 1926, 85. [Си. также: К очи и Н. е.. Векторное и теиэориое исчисления, изд. 6, ГОНТИ, 1938, стр. В9.- Прим. перев.]

Наконец, уравнение (6) п. 20.13, которое следует из уравнения состояния, дает

ар , ае , ар as

as ds dS ds

dg . dp dS

dn as ая

(8) (9)

Соотношение (8) и (9) можно использовать для исключения др/дп и dp/dS из уравнений (4) и (5). Тогда уравнения (4) - (7) будут представлять собой систему четырех совместных линейных алгебраических уравнений для определения четырех неизвестных величин

dq, dqn dQ dS dn dn dn dn

(10)

которые являются производными от q qn, Q, S no направлению нормали к кривой С.

Если эту систему решать с помощью определителей, то получим

dqs/dn dq /dn dQ/dn dS/dn 1 ....

После преобразований найдем, что эти определители соответственно равны

Ai=-ql (ql - с*), Аг = - 9.<7п (<7 - с') ,

Аз = Qqn А =<7 (9п-с*)

Ч' л- л l п п Ч

ds дЯп

qnMql + ql.) + {ql-c)

di+ж- Ч-Ч. - Чпх. {ql + с') + <7,х„ (с^ - q%) dq, 1 , 1 ар

Следуя Мейеру ), поставим вопрос о том, существуют ли такие линии С, вдоль которых уравнения движения (4) -(7) не позволяют определить нормальные производные (10) и, следовательно, также производную др/дп.

Ясно, что такой случай будет иметь место тогда и только тогда, когда величины (11) являются неопределенными, т. е. когда все определители Afc (А = 1, 2, 3, 4, 5) обращаются в нуль. Необходимое условие состоит в обращении в нуль определителя А] (следовательно, также и Д5), что дает qn = 0 или д„= ±с. Если qn = 0, то все определители обращаются в нуль, и тогда кривые С будут линиями тока. Мы вернемся к этому случаю в дальнейшем. Если же

q.= ±c, (12)

то имеем А1 = Аг = А5=0, в то время как условия Аз = А4 = 0 в комбинации с равенством (12) дадут единственное дополнительное уравнение

п >-п iizL v (r-rfl\

Q ds

(13)

Это уравнение вместе с равенством (12) не содержит производных по нор-ыали к кривой С, а также кривизну Хд ортогональной кривой N.

В частности, течение, в котором имеются разрывы нормальных производных давления, плотности, скорости и энтропии вдоль некоторых

) Meyer R. Е., The method of characteristics for problem of compressible flow involving two independent variables. Sixth Intern. Congress for Applied Mechanics, Paris, 1946, Quart. J. Mech. and. Appl. Math., I (1948), 196-219.