= tg(9H)-

Эта формула показывает, что линия Маха, вдоль которой параметры течения (т. е. q, р, S) постоянны, должна быть прямой линией (см. п. 20.50).

В статье Мейера (см. примечание к стр. 604) показано, как к уравнениям (13) - (16) можно применять метод численного интегрирования, развитый Массо'). Этот метод появился раньше методов, которые развивались Буземаном и другими авторами. Подробности этого метода можно найти в статье Мейера *).

) Massau J., Memoire sur Iintegration graphique des equations aux deriveis par-fielles, Ghent, 1900-1903. См. также Enzykl. d. Math. Wiss., 11, 3 S. 159.

*) Изложение современного конечно-разностного метода характеристик, приспособленного к расчету на электронных вычислительных машинах, см. в работах: Ч у ш-к и н П. И., Затупленные тела npocToii формы в сверхзвуковом потоке газа, Прикл мат. и мех., 21, вып. 3 (1960), 927 - 930, Кацк о ва О. Н., Н ау мо ва И. Н.. Ш мы г-левский Ю. Д., Шулишнина Н. П., Опыт расчета плоских и осесимметрнчных сверхзвуковых течении газа методом характеристик. Изд-во Вычислительного центра АН СССР, 1961.-Лриж. перев.

кривых, на которых выполняется условие (13), является течением, не противоречащим уравнениям движения. Указанные кривые называются характеристиками, или линиями Маха. Возможность существования указанных разрывов на линиях Маха отличает сверхзвуковое установившееся течение от дозвукового установившегося течения.

Следует подчеркнуть, что характеристики, определенные здесь условием (12), представляют собой те же самые кривые, которые были рассмотрены в п. 20.41.

Другое условие обращения в нуль определителей hh есть, как нетрудно видеть, условие qn = 0. Подставляя это условие в уравнения (4) -(7), получим

dq, \ др 2 1 /14ч

+ Q.x = 0, (15)

§-0. (16)

Эти уравнения представляют собой уравнения движения вдоль линии тока, уравнение неразрывности и исходное условие постоянства энтропии вдоль линии тока.

Эти уравнения показывают, что линии тока также обладают некоторыми характеристическими свойствами. Поскольку вышеприведенные уравнения (14) - (16) не содержат производных dq,ldn и дЗ/дп, на линиях тока могут иметь место разрывы этих величин, которые распространяются со скоростью газа. Такие разрывы соответствуют наличию вихря в потоке (см. п. 20.10). Однако обычно энтропия и полная энергия бывают известны на каждой линии тока, следовательно, вихрь определяется уравнением Крокко (3) п. 20.10, и тогда линии тока не будут уже иметь характеристических свойств.

Итак, оказывается, что единственными линиями, на которых уравнения допускают разрывы нормальных производных, являются линии Маха и линии тока. Неопределенность нормальных производных на этих линиях имеет место для производных любого порядка, как это можно доказать, дифференцируя уравнения по п любое число раз.

Из равенства (12) следует также, что угол между линиями Маха и линиями тока есть угол Маха р = arcsin (c/q). Таким образом, если 9 представляет собой угол наклона линии тока к оси х, то наклон линии Маха определяется формулой

В случае осесимметричного движения надо рассматривать кривые С и N, лежащие в какой-либо меридиональной плоскости. Пусть касательная в точке Р образует угол Э с осью и пусть о - расстояние точки Р от оси. Тогда единственное изменение в полученных выше уравнениях, связанное с осесиммет-ричностью течения, будет состоять в том, что в левые части уравнений (6) и (13) добавятся соответственно члены qR и cR, где

(лР - q, sin 9 -f 9 cos 9.

20.71. Теорема единственности. Рассмотрим установившееся адиабатическое плоское сверхзвуковое течение.

Определение. Криволинейный многоугольник, образованный дугами, каждая из которых является либо линией Маха, либо линией тока, либо

звуковой линией i), называется характеристическим, многоугольником.

Рассмотрим границу между областью, где движение (определяемое скоростью, плотностью или давлением и энтропией) равномерно, и областью, где нет линий, на которых нормальные производные некоторого порядка разрывны. Такая граница должна быть характеристической ломаной.

Далее, если заданы два течения, которые не имеют конечных разрывов скорости, 365. плотности И энтропии, одинаковы в какой-

либо одной области, но различаются в другой, то границей этих областей должна быть характеристическая ломаная.

Определение. Обыкновенной линией называется некоторая кривая, которая не пересекает какую-либо линию Маха или какую-либо линию тока более чем в одной точке.

На обыкновенной линии уравнения движения позволяют определить величины нормальных производных любого порядка от q, q, S для любого произвольного непрерывного распределения самих этих величин на этой линии.

Теорема единственности. Состояние сверхзвукового течения (т. е. значения переменных q, q, S) вдоль некоторой дуги ав обыкновенной линии определяет единственным образом поле течения внутри достаточно малого характеристического многоугольника, который содержит дугу ав.

Доказательство. Рассмотрим два течения Fi и F, которые имеют одинаковые состояния движения (т. е. одинаковые величины q, q, S) вдоль дуги ав некоторой обыкновенной линии.

Из определения обыкновенной линии следует, что для течений f, и Fi переменные q, q, S можно разложить в окрестности линии ав в один и тот же ряд Тейлора. Следовательно, течения /= , и f j будут одинаковыми в малой конечной области, содержащей ав. Но любую такую область можно расширить до некоторого характеристического многоугольника, что и требовалось доказать.

Теорема единственности утверждает, что состояние движения на линии ав определяет единственным образом течение внутри четырёхугольника Маха abcd (рис. 365), ограниченного парой линий Маха, проходящих через точку Л, и парой линий Маха, проходящих через точку в; при этом предполагается, что здесь не встречаются звуковые линии.

) Звуковая линия есть линия, иа которой скорость равняется критической скорости звука с*. Такая линия обычно является границей между дозвуковой и сверхзвуковой областями течения; см., например, критическую кривую внутри сопла Ринглеба (п. 20.33) ли в течении вихря (п. 13.80).

20.80. Течения, зависящие от времени. Рассмотрим некоторое течение, зависящее от времени t и от одной пространственной координаты г - расстояния от фиксированного начала координат. Обозначим через q скорость в направлении возрастания г. Тогда уравнения движения и неразрывности примут вид

дд 1 дд 1 др

dt дг ~ Q дг

ж Wf + -}-

(1) (2)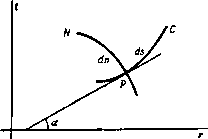

Рис. 366.

где V = 1 для одномерного течения (например, течение вдоль трубы); v = 2 для двумерного течения с круговой симметрией (например, плоский источник) и v =3

для трехмерного течения со сферической симметрией (например, случай пространственного источника). Сделав замену переменных (предложенную Риманом)

получим

дч) с^ dQ 1 др ди> dQ

Q дг

Q dt

Тогда уравнения (1) и (2) можно записать так:

dt dr dr dt dr dr

Сложение и вычитание этих уравнений дает

{( + q) + (q + c)- (a+q) =

(v-\)cq

((d-(7) + (9-c)-(0)-9)=----

(4) (5)

Как и в п. 20.70, представим себе, что плоскость (г, t) покрыта двумя семействами ортогональных кривых С к N. Пусть ds и dn являются соответственно элементами дуг кривых С и в точке Р и пусть касательная в точке Р к кривой С образует угол а с осью г (рис. 366). Тогда

ds+idn = e-(dr + idt),

и, следовательно.

d . а , d

= sina4-cosa

а д

- cos а

sina

аг di дп

Таким образом, уравнение (4) эквивалентно уравнению

\sina+(q + с) cos а] tSl + (cos a-iq + c) sin a] = - .

Это уравнение не позволяет определить нормальную производную e{ -\-q)/dn, если направление кривой С выбрать так, чтобы вдоль С выполнялось уравнение

cos а - (7с) sin а = О

ИЛИ

Ciga = = q + C. (6)

Тогда наше уравнение примет вид

ajc) (v- ij (7)

Итак, в плоскости г, t разрывы нормальной производной от функции (О + <7 перемещаются в направлении, нормальном к кривым С, со скоростью д + с, определяемой формулой (6). Это означает, что в физической плоскости эти разрывы распространяются со скоростью д + с, т. е. относительно газа со скоростью с. Следовательно, в соответствии с определением из п. 20.41 характеристиками здесь будут тoчки^) окружности или сферы в соответствии с V = 1, 2, 3.

Аналогичное исследование, проведенное с уравнением (5), показывает, что разрывы нормальной производной от функции ш - д перемещаются со скоростью д - с. Это определяет второе семейство характеристик.

Из формул (3) видно, что полученные выше результаты имеют место всегда, когда величина = др/дд является положительной. Следовательно, в рассматриваемом случае характеристики существуют как в дозвуковом, так и в сверхзвуковом течении.

В случае одномерного течения из уравнения (4) и (5) сразу же получим результаты Римана, а именно: 1) величина ч> + д остается постоянной для некоторой геометрической точки, движущейся со скоростью д + с, 2) величина О) - 7 остается постоянной для некоторой геометрической точки, движущейся со скоростью д - с. В дозвуковом течении эти две скорости имеют противоположное, а в сверхзвуковом течении - одинаковое направление.

ПРИМЕРЫ К ГЛАВЕ 20

1. Пусть £ -внутренняя энергия газа, S -энтропия. Показать, что

дЕ дЕ

2. Построить график, связывающий давление р и скорость д в изэнтропическом течении вдоль линии тока, и показать, что эта кривая имеет точку перегиба при д=с*.

3. Показать, что в изэнтропическом течении вдоль линии тока имеет место соотношение

(Y+1)- (Y-1)M*

где Q* - плотность при д - д*=с* и 1Л* = д/с*.

4. Получить уравнение Бернулли в следующей форме:

где

** = (Y-1)/(Y+1)-

6. Доказать, что для плоского установившегося безвихревого течения имеют место уравнения

ди dv d(Qu) , dJQv)

ду~дх~ ~д^~дГ~

6. Используя потенциал скоростей

) Или, вообще говоря, плоскости, перпендикулярные к направлению оси г.

где

хдф/ах=-fаф/(?9, я,аф/ая=аф/ав,

f=[l-(2p+l)T](l-T)-2P-i.

8. Рассмотреть второе решение (3) п. 20.32 для уравнения плоскости годографа при т= - 1 и показать, что в этом случае

~ = (и-г) е^®-г (2р+1) (In т-2.в) + 2фе.

Доказать, что в данном случае кривые постоянной скорости представляют собой трохоиды, полученные качением окружности радиуса а(1--Р) вдоль линии *=e(l-f Р)4-(2р+1) In т, причем трохоида описывается точкой, лежащей иа конце радиальной линии длины a(p-f-T~i).

9. Доказать, что в плоскости годографа огибающая трохоид из примера 8 имеет уравнение

. 2 0 (1-т)[(2р+1)т-1]

tg e=-2p+i)T+ip -

10. Показать, что в установившемся плоском сверхзвуковом течении в некоторой точке Р, где местная скорость звука равна с, можно определить нормали к характеристикам с помощью следующего геометрического построения. Надо из точки Р провести отрезок PQ, представляющий собой вектор скорости. Далее, провести окружность с центром в точке Р и радиусом с и построить другую окружность на отрезке PQ, как на диаметре. Тогда если Aj и N2-точки пересечения этих двух окружностей, то нормали к характеристикам представляются линиями PAi и РЛг-

11. С помощью уравнении (5) и (6) п. 20.43 доказать что если Ci и С2 являются характеристиками в некоторой точке Р, то касательная в точке Р к изображению характеристики Cl в плоскости годографа будет параллельна нормали к характеристике Сг в точке Р в физической плоскости. Доказать аналогичный результат для случая, когда характеристики Ci и Cj меняются ролями.

12. Рассматривается установившееся безвихревое плоское сверхзвуковое течение. Пусть в плоскости годографа построен некоторый треугольник ОАО, причем его вершина О находится в начале координат, а Р-точка на стороне AD. Этот треугольник построен таким образом, что отрезок ОР представляет собой вектор скорости в точке Р' в поле течения, РД-местная скорость звука, 0D -скорость i/max. а угол А является прямым. Проведем далее прямую линию PC, параллельную стороне АО, до пересечения ее со стороной 0D в точке С. Доказать тогда, что:

1) AP/AD = k [см. формулу (4) п. 20.42);

2) ОС представляет собой скорость с*;

3) лииия APD параллельна нормали к характеристике в точке Р';

4) линия APD является касательной в точке Р к изображению в плоскости годографа другой характеристики, проходящей через Р'.

13. Используя пример 12, показать, что точка Р описывает эпициклоиду, которая получается качением окружности, построенной на CD, как на диаметре, по неподвижной окружности с центром в точке О и радиусом ОС. Доказать что в установившемся безвихревом плоском сверхзвуковом течении годограф любой характеристики представляет собой эпициклоиду, полученную качением окружности диаметра Ятлх-* по неподвижной окружности радиуса с*.

14. Для случая сверхзвукового обтекания угла показать, что в обозначениях п. 20.50 число Маха определяется формулой

М =1+tg (*в+е).

доказать, что в сжимаемом дозвуковом течении с такой же циркуляцией радиальная и окружная составляющая скорости равны

Доказать на основании этого теорему Кутта-Жуковского для подъемной силы профиля. Показать также, что сила сопротивления в этом случае равна нулю. 7. Показать, что замена переменных вида

dk I dx

где ---* 1 при т -> О, приводит к следующим уравнениям в плоскости годографа:

/ sin fi \v/(v-l) 8W=[ Y cos2n J

фи отклонении

/у-со8 2цо Y-cos2fi

20. В примере 19 доказать, что при отклонении потока иа угол 9 скорость V определяется формулой

где Vo - скорость набегающего потока.

21. Показать, что дав.1еиие за плоским скачком, в котором поток отклоняется иа угол в, приближенно равно

Pi = Po(l-2yBcosec 2fio).

22. Показать, что в случае ударной волны, рассмотренной в п. 20.60, действительно имеет место увеличение энтропии, которое приближенно равно

Y -Y rQ У 12 KdoJ

где приближенно принято Aq/qo= 28 cosec 2fio.

2S. Используя обозначения п. 20.60, доказать, что

24. Газ совершает установившееся параллельное сверхзвуковое течение в прямой трубе. Пусть давление внизу По течению больше, чем давление вверху по течен1Ю.

15. Рассмотреть обтекание угла (см. п. 20.50) в случае, когда набегающий поток имеет критическую скорость с*, н доказать, что тогда уравнение линий тока имеет вид

r=ro(cosA8)- /*,

где Гр-некоторая постоянная. Показать отсюда, что линии тока представляют собой подобные кривые с центром подобия в вершине угла.

16. Построить методом характеристик полную картину течения При обтекании угла в случае, когда набегающий поток имеет критическую скорость с* и когда угол а между второй и первой сторонами угла настолько велик, что поток не достигает этой второй стороны угла.

17. В течение расширения около выпуклой ломаной линии воздушный поток отклоняется иа малый угол On у я-го излома (я=1, 2, 3, ...). Если р„-давление, ц„ - местное число Маха после обтекания я-го излома, то доказать, что приближенно выполняются равенства

-=1 2ув cosec 2fx .

Vn = Vn-l - -Y [(у +1) secVn i-21.

18. Показать, что если в предыдущем примере обтекаемая линия является гладкой, то

= -4-(Y + l)secV+l. Отсюда Доказать или проверить, что

е=/(ио)-/(ц).

19. Если обтекаемая линия в примере 18 является гладкой, то доказать или проверить, что

1 dp

Р g (1*)

Ро

где

V/(Y-1)

гоо V-1 L VQooy J Ooo

Ti (Y + l) Too

где Poo. Qno Too-соответствующие значения параметров торможения.

26. Используя метод наложения течения с постоянной скоростью, вывести соотношения для косого скачка уплотвеиня нз соотношений для пряного скачка уплотнения, рассмотренного в примере 24.

27. В одномерном теченяв газа давлеяяе является функцией плотности. Получить уравнения этого течения в следующей форме:

28. Газ течет параллельно оси х. Частица находится в точке х в момент < и в точке Хо в момент / = 0. Доказать, что

J a* дЧ др О ~дт dfi дт

где

Q dx.

20. Показать, что потенциал qi, рассмотренный в п. 20.30, удовлетворяет сдедух>-щему линейному дифференциальному уравнению:

30. Давление, плотность я нормальная составляющая скорости с каждой стороны стационарного косого скачка уплотменвя имеют соответственно значеняя ро, Qo. woPt. Qi, to,. Вывести соотношения

Qim=QiWi=m,

Ро-Pi = n(wj-Wo). У (.Po+Pi)=m (Щ+Щ),

где у-показатель адиабаты.

Если Со и Cl значения скорости звука с каждой стороны этого скачка, то доказать равеяство

clc\ = wi--J-[.y*~l)WoWi (Wo-*!).

Показать, что тогда должен возникнуть прямой скачок уплотнения, фронт которого перпендикулярен потоку и за которым течение становится дозвуковым. Доказать, что

Др = 0оио^1-. AQ = eo(7ii-l) . ttioai=c a.

25. Показать, что для прямого скачка уплотнения, рассмотренного в примере 24, имеют место соотношения

Pi... Y+ V + 1

ПРИЛОЖЕНИЯ

Н. Н. Моисеев

ПРИЛОЖЕНИЕ к ГЛАВЕ 2 АФИННЫЕ ОРТОГОНАЛЬНЫЕ ТЕНЗОРЫ

1. Определение тензора. Пусть через {xi, х^, Хз} обозначается точка в трехмерном евклидовом пространстве, а через х? (/= 1, 2, 3) -единичные векторы декартовой системы координат.

Рассмотрим две декартовы системы координат {х?} и {у?}, имеющие общее начало. Положение одной системы координат относительно другой задается таблицей направляющих косинусов

а -= cos (у?, х5)

(очевидно, что а^Фа), i, /=1, 2, 3.

Среди девяти величин направляющих косинусов независимых только 3, так как имеют место шесть следующих соотношений:

f О, если 1фк (условие ортогональности), 4j0.jiajh- (условие нормированности).

Пусть а -некоторый вектор в смысле определения п. 2.10; тогда

а = 2 х?а, = 2 ylah (2*)

где числа ai и а] называются компонентами вектора а. Компоненты Oj и а] связаны между собой соотношениями:

а; = 2 ауоо.

4, - (3*)

aj = Zaiaij.

Эти соотношения позволяют ввести новое определение вектора: вектором а называется тройка чисел [а^ а^, аз}, определенная в любой декартовой системе координат таким образом, что при переходе от одной системы координат к другой числа Oj преобразуются по формулам (3*).

По аналогии с этим определением введем определение аффинного ортогонального тензора: тензором л называется тройка векторов {pi, Рг, рз}, определенных в любой декартовой системе координат таким образом, что при переходе от одной системы координат к другой векторы pt преобразуются по формулам

Pi=2P;ao- (4*)

Векторы Pi называются векторными компонентами тензора п. Так как каждый вектор Рг может быть представлен в виде

Pi= 2?Р1/.

то тензор л определяется матрицей

/Ри Ри P\i\ п= Ри Pvi Ри \Pti Рп Раз/

Числа ptj называются скалярными компонентами тензора л. Пусть в любой системе координат определена матрица n=[pij}, тогда имеет место следующая теорема.

Теорема. Для того чтобы матрица я определяла тензор, необходимо и достаточно, чтобы при переходе от одной системы координат к другой числа ptj преобразовывались по формулам

= S Рулада.*- (5*)

Доказательство. Для доказательства необходимости предположим, что я -тензор. Следовательно, его векторные компоненты pj преобразуются по формуле (4*). Запишем вектор pj в системах координат (х?)

и (уЬ-

а вектор Pi в системе координат {у'):

Согласно предположению, векторы pi и Pj связаны формулами (4*), которые мы перепишем в виде

HO поскольку py -вектор, то числа р% и ру связаны формулами

Р*) = P;fc0.ft-

Таким образом,

Pi-SySPi.= S y PjhaijO;h-

il к

Сравнивая множители при единичных векторах с одинаковыми индексами, получаем формулу (5*).

Для доказательства достаточности следует выполнить указанные преобразования в обратном порядке.

Пример. Если в любой системе координат задана матрица / в виде

/1 О 0\ / = (0 1 О \0 О 1,

то матрица / - тензор.

Доказательство этого утверждения предоставляем читателю. Матрица / называется единичным тензором.

Пусть n = {pij} и Q= {(/jj} -тензоры; тогда очевидно, что матрица {РчЯи) также является тензором. На этом основании мы можем определить сумму двух тензоров аналогично сумме двух векторов: тензор S называется суммой двух тензоров я и Q, если его скалярные компоненты образованы по правилу

Sij = Pij+qtj

Симметричным тензором называется тензор, скалярные компоненты которого удовлетворяют условию

Антисимметричным тензором называется тензор, у которого компоненты удовлетворяют условию

Pij= - Pp.

Легко видеть, что всякий тензор можно представить в виде суммы симметричного и антисимметричного тензоров:

я = {Pij} = {у (Ри + Рл)} + {j {Ри - Рп)

Если а -скаляр, то величина ая определяет тензор, компоненты кото-рого имеют вид {ари).

2. Диады. Определим диадное произведение двух векторов (или диаду) а;Ь следующим образом:

(6*)

azbi афг афз)

Нетрудно убедиться, что матрица [aibj] представляет собой тензор. В самом деле, поскольку а и b векторы, то их компоненты преобразуются по формулам (3*), следовательно,

а\Ь] = 2 asbjaisajr.

г

Заметим, что диадное произведение некомутативио, т. е.

а;Ь Ф Ь;а.

Любой тензор можно представить в виде суммы трех диад. Для того чтобы в этом убедиться, отметим, что справедливо равенство

(Ри Pit PisN ООО ООО Следовательно,

л = {Ри}=2х?;Р| (7*)

В частном случае единичный тензор (или единичная диада) имеет вид

Если тензор л можно представить в виде

я = а,;Ь,-Ьаг;1н + аз;Ьз,

то сумма

Ь1;а, + Ьг;аг + Ьз;аз определяет тензор Q, компоненты которого задаются формулами

gij = Pji-

Подобно тому как любой тензор можно разложить на симметричную и антисимметричную составляющие, любую диаду можно представить как суперпозицию симметричной и антисимметричной частей:

а;Ь = I (а;Ы- Ь;а) +1 (а;Ь - Ь;а).