Каждому такому направлению будет соответствовать вектор pi, определенный, согласно (2*), формулой

p; = Pia j, (3*)

где

Рх, = Pi-

Но формула (3*), которая определяет векторы р1, заданные в системе координат (j/i, У2, Уз), через векторы рь определенные в системе координат {Xi, xz, хз), как раз и является определением тензора (см. приложение к главе 2). Тройка векторов (р р2, рз) называется тензором напряжений и обозначается буквой П. В матричной форме этот тензор имеет следующий вид:

/ Рч Рп Pз^ П= Pti Ргг Ргз

\Ри Р32 P33J

Скалярные компоненты рц являются нормальными напряжениями, а компоненты Pij (t Ф j) определяют касательные напряжения.

3) Тензор П является симметричным тензором (р<л = рм). Это утверждение носит название теоремы взаимности. Подобно тому, как из принципа Даламбера для сил непосредственно следовал тот факт, что напряженное состояние описывается тензором П, теорема взаимности является прямым следствием принципа Даламбера, записанного для моментов сил.

Для доказательства этого рассмотрим равновесие малого равностороннего тетраэдра. Напищем условие равенства нулю моментов относительно вершины тетраэдра, учитывая при этом только малые второго порядка:

г X p S = 2 Гг X piSt,

Г X р„ = 2 г< X PiCn (4*)

или

где Г( -радиусы-векторы центров тяжести граней Sj тетраэдра, а г -радиус-вектор центра тяжести грани S.

Умножим обе части равенства (2*) на г векторно слева и вычтем из результата равенство (4*); тогда

2(г-г,)хр,а„,= 0. (5*)

Обозначим через х[ проекцию вектора г -rj на ось х^. В силу симметрии очевидно, что

4 ) = 4=> = х'з'> = /. х^>0, 1Ф1.

Таким образом, г -Г( = /х?; кроме того, ап1 = Опг = Опз-

Принимая все это во внимание, мы приведем равенство (5*) к виду

2xiXpi = 0.

Умножим это равенство скалярно на хЦ. Заметим, что (х* х р*) х1 = О, поэтому, полагая последовательно А= 1,2,3, мы получаем следующие равенства:

(x;xp,)xj-f(x;xp,)xj = 0, (x,xp,)xj-l-(xjxp,)xj = 0, (х,хр.) xj+(xjxp,)x = 0.

Раскрывая смешанные произведения, мы получаем равенства

Pl2 = P ; Pl3=P3i; P23 = PS2i

что и требовалось доказать.

4) Рассмотрим частный случай идеальной жидкости, т. е. жидкости, в которой касательные напряжения отсутствуют. Это означает, что вектор напряжения р„ коллинеарен вектору нормали. Положим

Рг, = - РпП°,

где р„ -некоторый скаляр. Подставим это равенство в формулу (2*); тогда

-р„п°=. - SpjOihx?.

Умножая это равенство скалярно на х? (/=1, 2, 3), мы получаем

Pi = Рг = Рз = Рп = Р-

Итак, величина нормального давления в идеальной жидкости не зависит от ориентировки площадки. Величина р в идеальной жидкости называется гидростатическим давлением. Тензор П в этом случае имеет следующий вид:

/-Р О 0\

П= о -Р О \=-рЕ, (6*)

V О О -р/

где £ -единичный тензор.

2. Тензор скоростей деформаций. Теорема Гельмгольца

1) Рассмотрим изменение поля скоростей жидких частиц при переходе от точки Яо к близкой точке Pi. Обозначим через Vg скорость жидкой частицы, которая в данный момент находится в точке Pq (радиус-вектор которой обозначим через Го). Обозначим через Vi = Vo-bdv скорость жидкой частицы, находящейся в точке Рц радиус-вектор которой обозначим через Tfl-f dr; тогда

dy=dviX\, d:;, = 2 (lijX./ да = 1 2. 3. (7*)

Три скалярные равенства (7*) объединим следующим векторным равенством:

dv = ()dr, (8*)

где

dxi dv2

dvi AFT

dvi дхг dv2 dx2

дхз дх.

(9*)

Равенство (8*) не зависит от выбора системы координат и в любой системе координат вектору dr ставит в соответствие вектор dv. Следовательно, иа основании теоремы о характеристическом свойстве тензора, матрица dv/dr, определенная равенством (9*), является афинным тензором второго ранга. Этот тензор называется производной вектора по вектору.

2) Всякий тензор может быть представлен в виде суммы симметричного и антисимметричного тензоров. Положим

(10)

где S- симметричный тензор,

2 V J

1 \ (dvj ач 1 \ \ 2 Удх^- дхз)

2 51 У

С

К

а^г al акз

а^з + dxi J

2 I, ахз + дхч.

а г.л

dxj

дУг дх.

а Г-антисимметричный тензор,

О

1 / dv2 dVj Л

2 l,aI7 а^гу

1 аоз at>i

2 V dxi ах, у

1 f dvi dv2 2 дх2 дх

О

1Л 1 / at)! а^з N ч , у 2 1 ахз axi;

2 К дх2 ах, J

j / at)2 at>3 л 2 V ахз ах2 J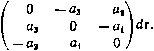

Тензор 5 называется тензором скоростей деформаций.

Умножение вектора dr слева на антисимметричный тензор эквивалентно умножению вектора dr слева на некоторый вектор. Легко проверить, что

аХ dr =

В нашем случае, как легко убедиться,

a = -i-rot V.

Отсюда, в частности, следует утверждение: для того чтобы течение было потенциальным, необходимой достаточно, чтобы тензор {dv/dr) был симметричным. Итак, мы приходим к следующему равенству:

Vi = Vo + ю X dr + S dr.

(11*)

Равенство (И*) имеет глубокий физический смысл. Оно показывает, что поле скоростей в окрестности данной частицы может быть разбито на три слагаемых. Первое слагаемое - это скорость, которую имела бы жидкая частица, если бы она двигалась поступательно. Второе слагаемое - это скорость вращательного движения частицы вокруг точки Р с угловой скоростью © = / rot v. Эти два слагаемых вектора v определяют скорость движения точки, принадлежащей частице, если бы частица жидкости была абсолютно твердой; сумма этих двух слагаемых называется скоростью квазитвердого движения. Третье слагаемое - это скорость так называемого деформационного движения, существование которого качественно отличает поле скоростей движения газа (или жидкости) от движения твердого тела.

Установленный результат носит название теоремы Гельмгольца. Окончательную формулировку этой теоремы мы примем в следующем виде: Всякое движение жидкости или газа в окрестности любой тонки можно разложить на квазитвердое движение и движение, вызванное деформацией.

3. Общее уравнение движения сплошной среды

1) Чтобы вывести уравнение движения сплошной среды, воспользуемся снова принципом Даламбера. Для этого выделим некоторую массу жидкости, заключенную в конечном объеме т. Пусть 5 - поверхность, ограничивающая этот объем, W - ускорение жидких частиц, q - плотность среды, F - вектор напряженности массовых сил, р„ - напряжение поверхностных сил. Применяя принцип Даламбера для выделенной материальной системы, получаем следующее уравнение:

- 5 ewdT4-5 eFdT-f 5 p dS = 0. (12*)

т т Н

Преобразуем входящий в это равенство интеграл по поверхности в интеграл по объему при помощи формулы Гаусса - Остроградского

J p dS= J divndT, (13*)

где

divn = 2- (14*)

Используя равенство (13*) и произвольность объема т, мы получаем дифференциальное уравнение

w = F-f--divn. (15*)

(Разумеется, в этом выводе мы предполагали, что все функции, определяющие и характеризующие движение, являются непрерывными функциями координат и имеют соответствующие производные.)

Это уравнение называется уравнением движения сплошной среды в напряжениях. Поскольку при его выводе мы не делали никаких предположений о характере тензора П, то уравнение (15*) справедливо для любой сплошной среды.

2) Рассмотрим частный случай идеальной жидкости. Идеальной жидкостью мы условились называть жидкость, в которой отсутствуют касательные напряжения и, следовательно, тензор напряжений имеет вид (6*), откуда

dpi др

Итак, если тензор П представляется в форме (6*), то мы получаем уравнения Эйлера:

w = F lvp, (16*)

которые вместе с уравнением неразрывности

-f Qdiv v = 0

для несжимаемой жидкости (q = const) образуют замкнутую систему четырех уравнений относительно четырех неизвестных: компонент вектора v и давления р.

4. Вывод уравнений Навье -Стокса

1) В общем случае произвольной вязкой жидкости тензор П (в силу его симметрии) определяется заданием 6 скалярных величин. Следовательно, для того чтобы поставить задачу, нам надо задать определенное количество связей

между компонентами тензора напряжений и компонентами вектора скорости и его производными. Эти связи в гидродинамике вводятся на основе опытных представлений и носят характер гипотез. Законность этих гипотез основывается на вековой практике, показывающей, что существует щирокий класс жидкостей и типов движения этих жидкостей, для которых эти гипотезы выполняются.

В основе наших представлений о взаимосвязи между полем тензора напряжений, полем скоростей и полем тензора dv/dr лежит закон Ньютона. Если движение происходит вдоль ocuxi и параллельно плоскости Xi,Xj, то, согласно закону Ньютона, сила трения (отнесенная к единице площади) равна

p,j = l {и,0,кФ}), (17*)

где 1 - коэффициент вязкости.

Справедливость этого закона (вернее, точность аппроксимации, которую он дает) подтверждена экспериментально для огромного большинства жидкостей и газов, когда они движутся в условиях, принятых в классической гидродинамике. Жидкости, которые подчиняются закону (17*), будем называть ньютоновскими. Разумеется, существуют исключения. К числу неньютоновских жидкостей относятся, например, жидкости типа полимеров, обладающие очень большими молекулами, у которых, к тому же, одно измерение значительно больше двух других. Точно так же в условиях большой разреженности любой газ перестает быть ньютоновским.

Итак, согласно закону Ньютона, компоненты тензора напряжений определяются компонентами тензора dv/dr, который, как мы указывали, может быть представлен в виде суммы (10*) симметричного и антисимметричного тензоров. Антисимметричный тензор Т описывает квазитвердое движение элементарных частиц жидкости, при котором силы вязкости равны нулю. Следовательно, компоненты тензора П могут зависеть только от компонент

тензора скоростей деформаций S.

Закон Ньютона формулирует для одного частного случая - плоскопараллельного движения - линейную связь между компонентами обоих тензоров. Поэтому для распространения этого закона на случай произвольного движения жидкости естественно постулировать линейную связь между

тензорами П и5 . Итак, первая наша гипотеза будет состоять в том, что искомая связь имеет вид

n = AS + B. (18*)

Выражение (18*) - это общее представление линейной тензор-функции. Здесь А - тензор, который зависит только от физических свойств среды и не зависит от характера движения и напряженного состояния (т. е. от компонент

П и 5) ). Тензор В может зависеть от компонент 5 и П, но формула (18*) до.1жна быть инвариантна относительно системы отсчета, следовательно,

В может зависеть только от инвариантов тензоров S и П, а из линейности (18*) сразу следует, что В может зависеть только от первых (линейных) инвариантов

тензоров S и П, т. е. от скаляров

Ниже мы используем этот факт.

1) В противном случае равенство (18*) определяло бы нелинейную связь между П и S

Вторая гипотеза будет состоять в предположении об изотропности среды: физические свойства среды не должны зависеть от направления и характера движения.

Эту гипотезу можно сформулировать еще и так. Главные направления

тензоров П и S должны быть коллинеарны. В самом деле, пусть это условие не имеет места; тогда в качестве осей координат в точке Р выберем главные

а

оси тензора S. Недиагональные элементы тензора 5 будут равны нулю. Если соответствующая компонента силы трения не равна нулю, то мы должны приписать ей знак плкх: или минус; выбор этого знака выделит некоторые преимущественные направления.

Из этой гипотезы сразу следует, что Л и fl в любой системе координат представляют собой диагональные тензоры. Более того, из равноправия любых направлений должно следовать утверждение о том, что тензорные эллипсоиды тензоров А и В имеют равные полуоси. Другими словами, тензоры А и В имеют вид

А = аГ, В=ЬЕ,

где а и - некоторые скаляры, причем скаляр а зависит только от физических свойств среды, т. е. от вязкости,

а = а{ц),

а скаляр b есть линейная функция первых инвариантов тензоров П и S, т. е.

bbo + biVy + biZpif (19*)

Итак, связь тензоров П и <S мы будем искать в виде

n = aS+(bo + biV\ + bi2Pii)E. (20*)

2) Найдем теперь коэффициенты а, Ь^, bi и Ь^ Введем еще одну гипотезу: закон (20*) должен как частный случай содержать закон Ньютона (17*). Рассмотрим плоскопараллельное течение вдоль оси xt (параллельное плоскости xi, xj). Тогда vivtixi, xj), vj = 0, tA = 0. Формула (17*) в этом случае дает

а из формулы (20*) следует, что

сопоставление этих выражений однозначно определяет коэффициент а,

а = 2\1.

Для определения скаляров Ь^, bi и 6} приравняем первые инварианты тензоров, стоящих в обеих частях равенства (20*),

2 Ри = 2iVv + 3bo + + 3bi 2 Pit- (23*)

Это равенство должно иметь место для любых форм движения, т. е. должно выполняться при любых значениях 2 Pti и Vv. Отсюда, приравнивая соответствующие слагаемые, мы сразу получаем

Ьо = 0, bi= -Vsi, bг = /з.

Итак, формула (20*) может быть переписана в следующем виде:

n = 2S + (V,2Pn-V,}iVf)£. (24*)

Это и есть искомая связь между компонентами обоих тензоров, однако в полученной форме это выражение еще неудобно для использования, поскольку в правую часть входит выражение 2 ри-

Выясним смысл величины 2 ри- Сила вязкости проявляется только при движении (при наличии градиентов скорости); следовательно, естественно предположить, что напряженное состояние в покоящейся вязкой жидкости будет таким же, как и в покоящейся идеальной жидкости. Но в идеальной жидкости

2Рп=-Зр, (25*)

где р - гидростатическое давление.

Введем еще одну гипотезу: постулируем равенство (25*), т. е. будем считать, что оно выполняется в движущейся вязкой жидкости. Тогда формула (24*) может быть переписана так:

П=2н5-(р + ЗДу)£. (26*)

Формула (26*) носит название обобщенного закона Ньютона.

3) Утверждение (25*), вообще говоря, необоснованно даже интуитивно. В самом деле, нет никаких оснований отождествлять давление, определенное формулой (25*), и давление, которое определяется уравнением состояния р = qRT, где R - газовая постоянная, а т - абсолютная температура. Более естественно предположить, что 2 Ри = - 3p + d, где d - некоторый скаляр, обращающийся в нуль, когда жидкость покоится (v = 0), и инвариантный относительно замены системы отсчета.

На этом основании примем /з 2 Ри = - р + Vv; коэффициент к носит название коэффициента второй вязкости. Впервые исследование явления второй вязкости было проведено Л. Д. Ландау ). Существование коэффициента второй вязкости было установлено экспериментально. Одновременно тоже экспериментально было показано, что этот коэффициент заметно отличается от нуля только в особых случаях (например, если в жидкости происходят химические реакции специального вида). Таким образом, в настоящее время существует твердая уверенность в том, что в рамках классической гидродинамики нет необходимости учитывать эффект второй вязкости. На этом основании мы сохраним выражение для связи между тензорами П и 5 в форме (26*).

4) Перепишем равенство (26*) в скалярной форме

f dVi , dvj \ dvi 2 ..

Равенства (27*) позволяют исключить компоненты тензора П из уравнения в напряжениях:

w = F+-divn. (28*)

Выражение для div П имеет вид

dp и v9 и V P2J vQ U V Рз/ jjO

) Си. Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, Гостехиздат, 1953, стр. 376.

Используя (27*) и (29*), мы приведем уравнение в напряжениях (28*) к следующей системе скалярных уравнений:

(30*)

dv3 -\

dX2)

Если жидкость несжимаемая и \i - величина постоянная, то система уравнений (30*) упрощается и в векторной форме может быть записана так:

(31*)

Уравнения (30*) и (31*) называются уравнениями Навье - Стокса.

В случае несжимаемой жидкости и независимости коэффициента вязкости от температуры уравнения (31*) совместно с уравнением неразрывности образуют замкнутую систему уравнений относительно трех компонент вектора v и давления р.

5. Уравнение энергии

1) Система уравнений Навье - Стокса и уравнение неразрывности содержат 6 неизвестных: три компоненты вектора скорости (и иг, з), плотность q, давление р и коэффициент вязкости \i. Коэффициент вязкости зависит только от температуры и считается обычно заданной функцией абсолютной температуры т:

= l(T). (32*)

Это уравнение содержит новое седьмое неизвестное - абсолютную температуру т. Абсолютная температура связана с плотностью и давлением уравнением состояния:

f (р, Q, Г) = 0.

В зависимости от характера среды функция f имеет ту или иную структуру. В случае газов условимся уравнение состояния брать в форме Клайперона:

P = qRT, (33*)

где R - газовая постоянная; в случае несжимаемой жидкости это уравнение заменяется условием

О = const.

(34*)

Итак, мы пришли к системе шести скалярных уравнений [три уравнения Навье - Стокса, уравнение неразрывности, уравнения (32*) и (33*)1, которые содержат 7 неизвестных: и uj. з. 0. Р, т.

Для того чтобы задача могла быть поставлена, необходимо еще одно уравнение.

Таким замыкающим уравнением является уравнение баланса энергии. Будем следить за некоторой массой жидкости, занимающей объем т {t). Закон сохранения энергии утверждает, что изменение энергии Е этой массы жидкости за единицу времени равно мощности Ai + Az внешних сил, притоку A3 энергии извне и мощности А^ внутренних источников энергии:

= А1 + А2 + Аз + А,. (35*)

Энергия Е массы жидкости состоит из двух слагаемых: Ei - кинетической энергии, т. е. энергии макроскопического движения частиц

Ei = Qv4x, (36*)

и £2 - внутренней энергии, т. е. энергии теплового движения молекул газа или жидкости.

Для газов в общем случае выражение £2 имеет довольно сложную структуру. Мы рассмотрим только случай совершенного газа , т. е. газа, внутренняя энергия которого определяется только поступательным движением молекул. Это значит, что энергия вращательных степеней свободы молекул пренебрежимо мала по сравнению с энергией поступательного движения. Для этого случая термодинамика дает выражение

£2 = / 5 cTpdx, (37*)

где Со - теплоемкость газа при постоянном объеме, связанная с теплоемкостью при постоянном давлении формулой

Ср = с„+; (38*)

величина / - механический эквивалент тепла (427 кгм/кал). Работа внешних сил складывается из работы массовых сил Л, и работы поверхностных сил Аз.

Ai= QFvdx, (39*)

т

=5p vdS, (40*)

где V -скорость движения жидких частиц, а S -поверхность, ограничи-ваюшля объем т.

Будем считать, что приток энергии извне происходит только за счет теплопроводности. Тогда, согласно закону Фурье, количество теплоты, поступившее через поверхность S в единицу времени (в механических единицах), определяется формулой

Лз = /JxI-d5, (41*)

где Л, - коэффициент теплопроводности.

Кроме того, будем считать, что внутри рассматриваемой массы жидкости нет никаких дополнительных источников энергии (например, за счет химических реакций).

Подставляя в уравнение (35*) выражения (36*), (37*) и (39*) -(41*), мы можем написать следующее (упрощенное) уравнение баланса энергии:

= \ qFv dT + jj p v dS + IX dS. (42*)

T S S

3) Уравнение (42*)-это уравнение баланса энергии в интегральной форме; для того чтобы получить дифференциальное уравнение, надо еще провести ряд преобразований. Прежде всего, заметим, что

(43*)

(Эти преобразования являются прямым следствием уравнения неразрывности d{Qdx)/dt = 0.) Далее преобразуем интегралы по поверхности, входящие в правую часть уравнения (42*), в интегралы по объему. Прежде всего

5 p v dS = 2 S PiV i d5 = 2 5 dS, (44*)

S i S i R

где a , = cos (n;c,) a = 2pг^У^x?.

Применив к этому интегралу формулу Гаусса - Остроградского, после очевидных вычислений получим

и PndS = 5 S div а; dt = 5 2 2 PiSjdx. (45*)

Аналогично преобразуем последнее слагаемое в уравнении (42*)

Л, = / XVr dS = J div (kVT) dx. (46*)

Используя формулы (43*), (45*) и (46*), преобразуем уравнение (42*) к виду

jFdT=0,

т

откуда, в силу произвольности объема т, получим следующее дифференциальное уравнение:

Q 4г (1с„Т+ т) = + 2 4 2 PJJ + div (XVr). (47*)

4) В уравнении (47*) надо заменить компоненты тензора напряжений следующими выражениями:

Р = -(P + Tjdivv) + 2,

Используя эти формулы и тождественное преобразование

(v.V)v = Vy-vxO,