V Xq =

dx ду дг и V W

Чтобы найти выражение (aV)q в декартовых координатах, заметим, что если

При такой форме записи легко видеть, что векторы а х Ь и b Х а имеют противоположные знаки, так как второй вектор получается из первого перестановкой двух последних строк в определителе; вследствие этого определитель меняет знак, но абсолютная величина его не изменяется.

Если ф = ф(х, у, z) -скалярная функция, то мы можем доказать с помощью формул п. 2.22 равенство

а из формулы (1) п. 2.15 получить следующее соотношение:

Уф = 10?ф) + ] Уф) + к(кУф). которое после простых преобразований принимает вид

так что векторный оператор V может быть записан следующим образом:

Если мы применим оператор У к вектору q, компоненты которого вдоль наших осей равны и, v, w, то получим равенство

откуда после перемножения скобок найдем соотношение

Применяя эту операцию к вектору 7ф, мы получим выражение для оператора Лапласа в виде

Ф дх* ду2 дг*

Аналогично

-( -f)H(t-)+k(-f)-

Последнее соотношение мы можем также записать символически следующим образом:

i j к

д д д

И, следовательно,

(aV),-l (<..g + ..1 ++

Наконец,

\,dxi dy* дг* J

Приведенные выше соотношения в декартовых координатах показывают, насколько компактнее и удобнее использование векторных обозначений, не зависящих от системы координат. Векторные методы являются мощным средством для получения общих теорем и позволяют сразу выяснить их внутреннее содержание. Но для того чтобы исследовать частную задачу и получить числовые результаты, почти всегда необходимо на некотором этапе вводить систему координат. Ясно, что часто бывает полезно вводить систему координат в самом конце решения задачи.

2.71. Другое обозначение для оператора д/дг. В предыдущем пункте мы показали, что оператор градиента может быть записан в виде

Следовательно, диадное произведение

= (i;i)+(j; j) + (k;k) = / (2)

равно единичному тензору, введенному в п. 2.16. Таким образом, если а-постоянный вектор, то

Кроме того, дт/дх = \, и, следовательно, имеет место равенство

дх дт дх дт

Эти результаты можно весьма просто обобщить. Так, если q = \u+iv + kw, то мы можем записать

Отсюда следует, что если а -постоянный вектор, то

(qa) = a, (6)

а если Т -некоторая скалярная функция переменных и, v и w, то

ди ~ди aq

и, следовательно.

= 2<Г(и, ).

дТ(1,ц) дТ dl дТдц dt ~ д% dt дц dt ~

Таким образом.

Полагая / = 1, получаем равенство

которое является векторным аналогом теоремы Эйлера об однородных функциях (второго порядка). Рассмотренное доказательство является совершенно общим и может быть применено к однородным функциям степени п; для этого в проведенном доказательстве число 2 надо заменить на п.

2.72. Криволинейные ортогональные координаты. Декартовы координаты точки определяются пересечением трех взаимно перпендикулярных плоскостей х = const; J/= const; z = const. Для некоторых задач удобно ввести другие системы координат, например сферические координаты, в которых положение точки определяется пересечением сферы г = const, плоскости ю = const и конуса 6 = const (рис. 43), или цилиндрические крординаты, в которых положение точки определяется пересечением двух плоскостей ;< = const, ffl = const и цилиндра q = const (рис. 44).

Чтобы вывести выражение для оператора V в такой системе ортогональных координат, предположим, что координаты точки заданы равенствами

* = /i ( 1. а, з), У = /г ( 1, 2, s), 2 = /з ( 1, 2, Us),

Из формулы (6), повторив рассуждения, приведенные в п. 2.33, можно получить следующее равенство:

= (ад) = (ЧоФ + (qqo) = Оо + Qo = 2q .

Легко показать, что если Го и г-радиусы-векторы фиксированной частицы жидкости в разные моменты времени, то имеет место равенство

д д; Го д

где через д; То/дг обозначено произведение д/дг; г^. Отсюда, в частности, находим соотношение

д; То д; г д; г . г д; Гр .q.

дт дто ~ дт ~ ~дТо' дт

Пусть 7-однородная скалярная функция второй степени относительно векторов икс . Это означает, что если 7 = 7{и, в ), а -скаляр, тогда

T(tu, /©)=/ 7(u,fi ).

Введем обозначения = /и; Т1 = в , и тогда

л) = /*Г(и, ),

где поверхности Ui = const, 2 = const, = const взаимно ортогональны. Если мы проведем поверхности, соответствуюш,ие значениям координат ы Uj, из и U,+би U2 + 6 2. з + быз. то получим фигуру, которая с точностью до малых первого порядка является параллелепипедом с ребрами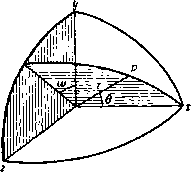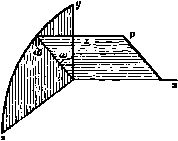

Рис. 43.

Р и с. 44.

hfiui, hibUi, htbus (рис. 45), где Л h, A3 являются функциями координат и находятся из соотношения

где

(ds) = {dx) + (dy) + {dz) = h\ {du,Y + h\ (dur + hi {dus)*.

и т. д. При этом надо учитывать, что произведения вида dudu пропадают вследствие ортогональности координат.

Пусть через it, ij, 13 обозначены единичные векторы в направлениях OA, ОВ, ОС, соответствующих возрастанию величин и„ 2. из- Эти векторы взаимно перпендикулярны и удов-0 В' летворяют всем соотношениям, выведен-

ным в п. 2.70 для векторов i, j, к.

Тогда, учитывая результаты п. 2.31 для скалярной функции ф, можно записать соотношение

И отсюда, использовав формулу (1) п. 2.15, получим равенство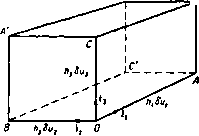

Рис. 45.

Таким образом, в криволинейных координатах оператор V имеет вид

/1 dUi hz du2 Л3 duj

Так как единичные векторы сами являются функциями координат, мы должны вычислить выражения вида Vxi, и Vli. Чтобы вывести первое из них, заметим, что из формулы (III) п. 2.3! следует равенство V X (Vui) = 0, а из формулы (I) -равенство Vu, = ii ii. С/.сювательно, из формулы (VII)

П. 2.34 получим соотношение

= 1, X

Vxi,

aft,

ft (Азии, ft,h2au2 Далее, нз соотношения (1) п. 2.34 получаем

Vl, = V(i2Xb)=i3(Vxi2)-U(Vxi3).

Следовательно,

I dhz 1 dhi 1 d(ft2ft3) (In hih2 dui ftifts dui Л|Л2Лз duj 1 hj (

Теперь пусть

q = ?iii + 92U + 93 3-Тогда нз формулы (IV) п. 2.34 следует равенство

Vq = 2V (<7A) = 2(</.Vi,+ ifcV(/,).

Это равенство приводится к виду 1

?q =

(-У.ЛзЛз) + (92Л3Л,) + (?зЛ1Л2) ] .

Так, если q= - V<p, то из соотношений (1) и (2) получаем формулу Далее,

* A,h2h3 I dui У А, auj au2 V Лг гУ з V л3 duJ J

(2) (3)

V X q = 2V X {g,h) = 21 - I, X + g, (V X i)l.

и. следовательно, после преобразования выражение для вихря можно представить в форме определителя

£=Vxq=

где

S = ?iii+ С2!2+Сз з.

Из формул (7) п. 3.10 [и (IV) п. 2.34 мы получаем следующее выражение для ускорения *):

Вычислим компоненту ускорения вдоль вектора i,. Мы имеем

Kdtji~ dt

) Это выражение помещено здесь для удобства изложения, но сначала следует прочитать а. 3.10 следующей главы.

Из формулы (I) получим равенство

а из формулы (4)-соотношение

(дх5)1 = <72Сз-</зС2 =

Яг Си ддгН . ддхН\ Яз Сt, Язз и dgihi\

Комбинируя последние три равенства, получаем выражение для компоненты ускорения вдоль вектора ii в виде

д<71 1 д<?, , 1 а(7, I dqi,

IF + лГ 9551 +9 ai++

А, La, \duj Аг\duj f Аз \duj J

Остальные компоненты ускорения можно выписать, пользуясь правилом симметрии.

Проиллюстрируем полученные результаты на примере сферических координат. В этом случае (см. рис. 43) можем записать равенства

* = rcos6; у =/ sin 0 cos ©; z = г sin 0 sin оо,

ids)* = {dx)* -Ь (dyY + (dzY = (d/- ) + (d0)*+r* sin 0 (dm).

Таким образом, если положить ы, = r; 2 = 0; из = <в. то мы получим

Л, = 1; А, = г; Аз = г51П0. (7)

Из равенства (3) следует соотношение

г sin в

Аналогично для цилиндрических координат

х = х\ у = о> cos ©; z = (в sin ©.

Полагая 1=*, 2 = ©. 3 = ©, мы получим Ai= 1; Л2= 1; Лз = й). Используя формулу (4), получим выражение для вихря в цилиндрических координатах в виде

где индексы обозначают направление соответствующего единичного вектора или компоненту вектора (см. также примеры 16, 17 к гл. 2).

2.73. Скорость изменения единичных векторов. В ортогональных криволинейных координатах (п. 2.72) мы можем вычислить производные dlr/ди, (г, s=sl,2,3) следующим образом. Согласно теореме Дюпена), линии

1) В е 11 R. J. т., Coordinate geometry of three dimensions, Lnd., 1926, ct 334 - 344. [Рашевский П. К.. Курс дифференциальной геометрии, ГИТТЛ, М., 195 стр. 267 - 268.-Лрцж. ред].

du, 1 dU2~ 3

Следовательно, Ц^-, откуда

dl, . dij . dhz . dhi

lл:r-гя;7-- 2577 -i

du2 duj du, dU2

Ho вектор dijduz параллелен ij, a вектор dU/dUi параллелен i,. Следовательно,

dUja.. di2ij dA, du2 hi du, du, Й2 du2

Кроме того, из равенства ii = ia X 13 мы полуаем соотношение

t 2 W : 1 i v=. [з.*!- iLl - rfc (9\

du, ~da, 3-t-2 X = vn,.

Из формул (1) и (2) мы можем получить производные dlr/dUs для всех значений /-, s= 1, 2, 3.

Эти результаты вместе с оператором

ft, du, ft2 du2 Лз 3 дают возможность весьма экономно вычислить любую V-операцию.

ПРИМЕРЫ К ГЛАВЕ 2

1. Пусть массы т, п сосредоточены на концах векторов а и Ь; доказать, что центр тяжести этих масс выражается вектором (та~\-пЪ)/(т-\-п).

2. Доказать равенства

ab = bu = axbx+iyby+azbz, (1)

(а + b)2=а2 -f- 62 + 2ab, (2)

а (b X с) -

3. Доказать равенства

я у г

Ьх by bz

Сх Су Cj

= [а b с]. (3)

(а4 Ь)х(а-Ь)=-2ахЬ, (1)

I а X b 2 = a2b2-(ab)2r=(a6-f ab) (а6-ab). (2) 4. Доказать равенства

ax(bxc)-l-bx(cxa) + cx(axb) = 0, (1)

(а х b) (с X d) = (ac) (bd)-(ad) (be) (тождество Лагранжа), (2)

a lb (с X d)]-b (a (c x d)l +c [d (a x b)] -d [c (a x b)) = 0. (3)

пересечения трижды ортогональной системы поверхностей представляют собой линии кривизны. Следовательно, кривые, вдоль которых изменяются или координата щ, или координата Ыа. являются линиями кривизны поверхности Ыз = const. Тогда нормали к поверхности в смежных точках линии кривизны пересекаются. Следовательно, когда мы движемся вдоль отрезка OA (см. рис. 45), нормаль h + dh пересекает нормаль 1з. Отсюда следует, что вектор dis перпендикулярен векторам ia и \з, т. е. параллелен вектору Следовательно, вектор dijdui параллелен вектору ii. Аналогично можно показать, что дУди параллелен вектору ij, и получить еще четыре подобных результата.

Пусть d& = hidui\i-ThidUiU-\-h3du3\z- Отсюда

ds , . ds , . ds . .

5. Доказать, что площадь треугольника, радиусы-векторы вершин которого равны а, Ь, с, равна модулю вектора

4-I(bxc)-f(cxa)-f(axb)l.

6. Доказать, что если Я,-скалярная, а г и s-векторные функции переменной /, п выполняются соотношения

d dr d\

d ds dr

d ds , dr

(rxs) = rx -+xs. (3)

7. Пусть имеется семейство поверхностей if -с, где ф -потенциал скорости, а постоянная с принимает ряд равноотстоящих бесконечно малых значений. Показать, что в любой точке скорость обратно пропорциональна расстоянию между соседними поверхностями в окрестности этой точки.

Доказать также, что если некоторая эквипотенциальная поверхность имеет точку самопересечения, то эта точка является критической точкой.

8. Пусть через ф(г, t) обозначен потенциал скорости; доказать равенство

dff = -dt-qdt

и показать, что дифференциальное уравнение линий тока имеет вид

drx Vф = 0.

9. Пусть ф н ф' -два решения уравнения Лапласа (п. 3.20) для области, ограниченной замкнутой поверхностью S. Доказать равенство

J 4>fdS=]if%dS.

(S) (S)

10. Пусть функция ф(х--й, у-\-к, z+t) записана в виде f(r--R), где

г = 1х+1у + кг: R = ih+ik + kl. Доказать, что теорему Тейлора можно записать в следующей символической форме:

Ф (г-Ь R) = ф (г)+(RV) ф (г)-Ь- (RV)2 ф (л).. .

П. Пусть 1[ = 1&х-[-1&у-\-к&г; доказать, пользуясь обозначениями п. 2.40, следующее равенство:

/ (П) = I (а б* + h6y+guz)+j (Adx + Ьбу+i&2) + k{g6x+ l&y + сдг).

где

ди dv dw

°=дх *=a7 =Ж-

А , di> ди , dw , dv , ди

и, следовательно, уравнение центральной поверхности второго порядка (см. п. 2.40) имеет вид

т(6х)+Ь (6у)+ с {liz)+2l6y&z+2gbz6x + 2hl>Miy=const. 12. Пусть q = l -l-Jt --kji(, ц = 1вж--]ву-!-кв ; доказать равенство

13. Доказать, что в любой точке Р движущейся жидкости существует в произвольный момент времени единственный триэдр с взаимно перпендикулярными осями, такой, что если этот триэдр движется вместе с жидкостью, то через малый промежуток времени &t углы между его осями остаются прямыми с точностью до членов первого порядка малости относительно Ы, н что угловая скорость вращения триэдра при движении его вместе с жидкостью равна i/o rot v, где v -скорость жидкости в точке Р. Доказать также, что если малая частица жидкости с центром масс в точке Р мгновенно отвердеет, не изменяя своего момента количества движения, то угловая скорость ее сразу после отвердевания равна 1/2 rot V тогда и только тогда, когда главные оси инерции отвердевшей частицы направлены вдоль осей упомянутого выше триэдра.

14. Используя тензорную форму теоремы Гаусса, доказать равенства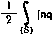

jJ (nq)qdS= 5 ((4V)q-fq(Vq)Idr. <S) (V)

2 2{nq)qlrfS=5 [q(4)-4xSldt.

(1> (2)

15. Пусть Я, Q H -ограниченные, непрерывные и однозначные функции переменных X, у, г в области, ограниченной замкнутой поверхностью S; доказать, что имеет место равенство

где /, т, я -направляющие косинусы внешней нормали к поверхности S.

Вычислить интеграл dS/p, распространенный по поверхности некоторого эллипсоида, где р-длина перпендикуляра, опущенного из центра эллипсоида на касательную плоскость.

16. Доказать, что в сферических координатах компоненты вектора вихря задаются формулами

°*Ч)г= .sine

(rotqL = (rot q)o = 4

дг Г 1

ддг

sin В а

17. Доказать, что в цилиндрических координатах справедливо равенств*

агф

ахг лТЛ^ ~

аш

(I) да со

18. Доказать, что в цилиндрических координатах компоненты вектора внхря имеют

гго.о^ Г д (д^а) дд~ (rotq), = -

0) L да

(rotq)~ = -4-

а (д^а) 1

(rot q)

dq;S ддх

10. Докаэлть, что если точка Р лежит на прямой, которая проходит через конец ект>ра а параллельно вектору Ь, то уравнение этой прямой имеет вид H = a-f-b/, где ц - ради \ с-вектор точки Р, а t - произвольный скаляр.

20. Показать, что уравнение плоскости, имеющей нормаль п и проходящей через иней вектора а, имеет вид

(т1-а)п = 0.

21. Показать, что если тензор, то уравнение ifi=const задает семейство центральных поверхностей второго порядка.

22. Доказать равенства Vxr = 0, Vr = 3-, Vr = r/r,

V(l/0=-V2(l/r) = 0.

23. Доказать, что в общих ортогональных координатах имеют место соотношения

и вывести выражение для (lV) q.

24. Показать, что члены в выражении (V; q) имеют вид

и отсюда вывести полное выражение для (V; q).

25. Доказать, что если Ф-произвольная диада, то справедливы равенства

V(qф) = qVФ + (ФV)q, (I)

Ф = (ФП i) + (Oj; ])Ч-(Фк; к). (2)

26. Доказать, что если а, Ь, с-произвольные некомпланарные векторы, а векторы а*, Ь*, с* выбраны так, что а*а = 1; b*b=l; с*с=1, а произведения ab*, ас* и т. д. все равны нулю, то выражение (а; а*) + (Ь; b*)-f (с; с*) есть единичный тензор.

27. Пусть U -единичный вектор. Дать геометрическую интерпретацию скалярному произведению их и доказать геометрически равенство

U (b-{-c) = ub4-uc.

Вывести закон дистрибутивности для скалярного произведения.

28. Рассматривая векторное произведение единичного вектора и и вектора

х = аХ(ЬХс) -ахЬ-ахс,

и используя результаты предыдущей задачи, показать, что х=0, доказав таким образом закон дистрибутивности для векторного произведения.

29. Используя обозначения п. 2.50, доказать равенства

5 V(ng)dS=jj V(qds). (S) (С)

30. Используя обозначения п. 2.72, доказать равенство

н вывести аналогичные соотношения для величин Аг и Ад. 31. Доказать равенство

а Ь с [аЬс] (pXq)= pa pb рс qa qb qc

32. Доказать равенства

V[(q;q)-y/7J=q(Vq)-qXg,

(q; q)-- iQ] } = -rX[q(Vq)-qX£].

(1) (2)