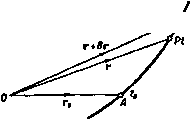Глава 3 УРАВНЕНИЯ ДВИЖЕНИЯ

3.10. Дифференцирование по времени. На рис. 46 показана действительная траектория жидкой частицы, находящейся в момент времени в точке А, которая имеет радиус-вектор Го относительно фиксированной точки О.

В момент времени / частица находится в точке Р, в момент i + 6t она находится в точке Q, радиусами-векторами этих точек являются г и г-Ьбг соответственно. Частицу, расположенную в точке Р, можно охарактеризовать скалярными функциями, такими, Qt*it как давление и плотность в точке Р, и векторными функциями, такими, как скорость и ускорение в точке Р.

Попытаемся получить производные по времени от таких скалярных и векторных функций. Прежде всего заметим, что радиус-вектор г отдельной частицы жидкости является функцией Рис- 46.

только времени /, так как ясно, что г

может зависеть только от времени / и некоторого фиксированного начального положения, например точки А. В п. 1.10 было получено равенство

ч-ж- <

Рассмотрим теперь, например, плотность q. Для частицы, находящейся в точке Р, плотность зависит только от радиуса-вектора г и времени t, так что

е=/(г, t).

Так как г является функцией только от времени t, то и плотность q является функцией только от времени t и, следовательно, мы можем найти полную производную dq/dt. Для ее вычисления воспользуемся следующей формулой из п. 2.71:

dQ df(T,t) dT df(T,t) df(r,t) f .

И, следовательно,

f f + lV)Q. (2)

Первый член в правой части этой формулы представляет собой скорость изменения Q по времени, если Р рассматривать как фиксированную точку, второй-скорость изменения q в момент времени / за счет того, что частица переместилась из точки Р в точку Q. Поскольку q-скаляр, то выражение (2) можно записать в виде

f-=t+q(VQ). (3)

те г лав т 3

Формула (3) определяет скорость изменения плотности при движении частицы жидкости. Если жидкость несжимаема, то плотность частиц жидкости не изменяется, поэтому справедливы равенства

=0. или J + q(VQ)=0. (4)

Если плотность Q постоянна, то уравнение (4) удовлетворяется тождественно.

Применяя подобный вывод к любой скалярной функции а, получим формулу

f = l?+4(Va). (5)

Чтобы найти скорость изменения вектора а, связанного с частицей, применим соображения, аналогичные соображениям, использованным при выводе соотношения (2); теперь получим формулу

l=t + (q)a. (6)

которую нельзя привести к виду (3).

Наиболее важным является случай, когда q представляет собой вектор скорости, скорость изменения которого есть ускорение частицы; из формул (IV) п. 2.34 и формулы (6) находим равенство

= +(qV)q = ?-fy(l,)-qXg. (7)

Применяя это соотношение к случаю прямоугольной декартовой системы координат, получаем равенство

+l + lr-+iw+k + ( lr + i+-)( +i +M. отсюда следует, что соотношение (7) эквивалентно трем уравнениям:

dw dw dw .dw , dw

Таким образом, в прямоугольных координатах справедлива следующая формула:

dt -дГ dx dy dz В векторной форме получим формулу

= + (qV). (9)

Рассматриваемую здесь операцию иногда называют индивидуальным дифференцированием, подразумевая под этим, что мы вычисляем скорость изменения некоторого количества, связанного с какой-либо движущейся частицей).

Некоторые авторы используют обозначение DIDt. Применяется, кроме того, термин убстанциональное, или материальное, дифференцирование.

3.20. Уравнение неразрывности. Если мы рассмотрим частицу жидкости бесконечно малого объема dx с плотностью Q в момент времени то масса этой частицы не может измениться при движении и, следовательно, можно записать уравнение

(QdT)-0. (1)

Это уравнение -одна из форм уравнения неразрывности, или уравнения сохранения массы. Если объем увеличивается, то плотность уменьп шается, и наоборот; таким образом, уравнение (1) всегда удовлетворяется.

Пусть через X обозначено какое-либо свойство, присущее единице массы и переносимое частицей жидкости при движении. Тогда для объема V, движущегося с жидкостью, т. е. состоящего всегда из одних и тех же частиц жидкости, получим равенство

(v) (v) (v) (v)

Другая точка зрения состоит в следующем. Рассмотрим фиксированную замкнутую поверхность 5, целиком лежащую в жидкости (рис. 47). Если п обозначает единичный вектор внутренней нормали к элементу dS, то количество жидкости, втекающей в единицу времени через границу в объем, заключенный внутри поверхности S, выражается в виде интеграла

W - (3) р„с. 47.

Масса жидкости, содержащаяся в объеме V, ограниченном поверхностью S, равна интегралу

Если предположить, что внутри поверхности S нет источников и стоков жидкости, то масса может увеличиваться только благодаря потоку через границу. Приравнивая выражение (3) и производную по времени от увеличения массы и применяя теорему Гаусса, получаем равенство

5 QdT= J oqndS = l- [ V(cq)dT.

(v) (8) (v)

Таким образом, находим уравнение

5 ( + V(Qq))dT = 0.

<v)

Так как поверхность S может быть заменена любой произвольной замкнутой поверхностью, проведенной внутри S, то в каждой точке должно выполняться уравнение*)

--fV(oq)=0, (4)

которое представляет собой другую форму уравнения неразрывности.

) Если \ Adx = Q для произвольного объема V, то Adx=0, так что

liiB \ Adx=0, т. е. Пт --AVAO.

--bq(VQ) + QVq = 0, f + eyq = 0. Vq=ln(l).

В случае несжимаемой жидкости dQ/dt = 0 [см. формулу (4) п. 3.10} и. следовательно, получим уравнение

Vq = 0, (6)

которое представляет собой уравнение неразрывности для несжимаемой жидкости; дивергенция Vq обращается в нуль.

Используя прямоугольные координаты (п. 2.70), уравнение (6) можно свести к виду

В особенно важном случае безвихревого движения получим равенство q= - V<p, и, следовательно, уравнение неразрывности (6) для безвихревого движения жидкости имеет вид

V4 = 0. (8)

или в прямоугольных декартовых координатах

dxi ау2 dzi

Уравнение (8) известно как уравнение Лапласа.

Из полученных результатов следует, что жидкость не может двигаться при произвольно выбранном законе распределения скорости. Для того чтобы движение было возможно, необходимо, чтобы удовлетворялось уравнение неразрывности.

В частности, для безвихревых движений жидкости потенциал скорости ф должен удовлетворять уравнению Лапласа.

3.30. Граничные условия (кинематические). Если жидкость находится в соприкосновении с твердой поверхностью или с другой жидкостью, с которой она не перемешивается, то, для того чтобы это соприкосновение сохранялось, необходимо выполнение кинематического условия, состоящего в том, что жидкость и поверхность, с которой поддержи--5i>--/i!fefcj*q вается соприкосновение, должны иметь одинаковую скорость, перпендикулярную к поверхности.

Р с. 48. Если мы обозначим через п единичный вектор

нормали, проведенный в точке Р поверхности соприкосновения, и через q - скорость жидкости, то в случае неподвижной твердой поверхности должно иметь место соотношение qn = О, выражающее условие того, что нормальные скорости равны нулю или, иными словами, вектор скорости жидкости повсюду касается неподвижной поверхности (рис. 48). Когда твердая поверхность движется, то должно выполняться равенство

qn = Un,

или

(q-U)n = 0,

где через U обозначена скорость точки Р поверхности (рис. 49).

Применяя теперь формулы (VI) п. 2.34 и (9) п. 3.10. мы последовательно находим равенства

Это равенство показывает, что скорость жидкости относительно поверхности перпендикулярна к нормали, т. е. касательна к поверхности.

Если две жидкости, которые не перемешиваются (такие, как воздух и вода), соприкасаются вдоль общей (геометрической) поверхности раздела S, то ясно, что для сохранения соприкосновения относительная скорость q - q снова должна быть касательна к поверхности 5 (рис. 50). С другой стороны.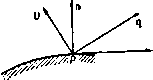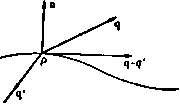

Рис. 49.

Рис. 50.

отметим, что в данном случае вид и движение поверхности S не известны до тех пор, пока не решена задача о рассматриваемом движении жидкости.

3.31. Граничные условия (физические). Только что рассмотренные кинематические условия должны выполняться независимо от каких-либо специальных физических предположений.

В случае невязкой жидкости, соприкасающейся с твердыми границами (неподвижными или движущимися), требуется выполнение добавочного условия, состоящего в том, что давление жидкости должно быть перпендикулярно границе.

В случае двух невязких жидкостей, имеющих поверхность раздела S, должно быть выполнено условие, заключающееся в том, чтобы давление было непрерывно на границе при переходе с одной стороны поверхности S на другую).

Для доказательства рассмотрим цилиндр (рис. 51), образующие которого перпендикулярны поверхности 5 и поперечные сечения которого dS представляют собой элементарные площадки, расположенные по обе стороны от поверхности S. Тогда если через р р' обозначить давления в двух жидкостях, то условие равновесия цилиндра выразится в виде

pdS - f.dS = 0, т. е. р = р',

поскольку, как показано в п. 1.30, объемные силы и массовые ускорения пренебрежимо малы по сравнению с остальными членами.

Таким образом, в случае воды, находящейся в соприкосновении с атмосферой, давление воды на свободной поверхности будет равно давлению воздуха, и если это последнее предполагается постоянным, то поверхность жидкости будет поверхностью постоянного давления.

Другим важным примером граничных условий является случай, когда поверхность S разделяет не две различные жидкости, а две области одной и той же жидкости и при этом имеется разрыв тангенциальной компоненты скорости на поверхности S, которая является вихревым слоем (п. 13.70).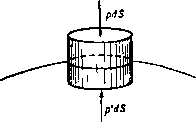

Рис. 51.

) Это давление следует видоизменить, если учитывать поверхностное натяжение (см п 14.5(1).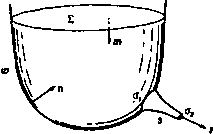

Такой случай имеет место в области воздушного потока позади крыла, где два потока с верхней и нижней сторон скользят друг по другу вдоль поверхности раздела, возникающей у задней кромки крыла. Тогда, если движение установившееся, из теоремы Бернулли следует равенство

и, так как р = р', мы должны иметь q = q. Таким образом, данная поверхность представляет собой поверхность разрыва направления скорости, а не ее величины.

В случае струи или некоторого потока внутри покоящейся жидкости, в которой давление можно считать постоянным, неразрывность давления внутри и вне струи показывает, что поверхность струи является поверхностью постоянной скорости.

В случае вязкой жидкости экспериментально доказано, что на твердой поверхности, соприкасающейся с жидкостью, относительная скорость равна нулю; это физическое условие необходимо учитывать при изучении движения вязкой жидкости.

Промежуточную поверхность между жидкостью и погруженным твердым телом можно рассматривать как вихревой слой, т. е. как поверхность разрыва тангенциальной скорости при переходе от жидкости к твердому телу (п. 13.70). В случае вязкой жидкости указанный разрыв скорости отсутствует.

3.32. Истечение из отверстия. Возвращаясь к вопросу, рассмотренному в п. 1.82, исследуем установившийся безвихревой поток жидкости, вытекающей через отверстие площади о, в стенке сосуда (рис. 52).

Рассмотрим плоское горизонтальное сечение Z сосуда, настолько удаленное от отверстия, что скорости течения во всех точках пересечения 2 с линиями тока можно считать одинаковыми и равными <7i. Пусть ш - единичный вектор нормали, проведенной к поверхности 2 внутрь жидкости.

Обозначим через 1 единичный век-Р и с. 52. тор внешней нормали к сечению Ог

в самом сжатом месте струи, где скорость равна qz. Пусть w обозначает поверхность стенки сосуда ниже сечения Z, S - поверхность струи между сечениями о, и ог- Рассмотрим жидкость, ограниченную полной поверхностью 2 + w + s -\- Oz; пусть п будет единичным вектором внутренней нормали в какой-либо точке этой поверхности.

Так как уя = О и так как течение безвихревое, то применение теоремы Гаусса [формула (7) п. 2.611 дает соотношение

5 q (nq) dS = - J (qV) qdT -j Vqdr=>-j J nq4S.

при получении которого использовались формулы (IV) п. 2.34 и (3) п. 2.61.

Теперь скалярная величина nq принимает на поверхностях Z, w, s, Oj следующие значения: j, О, О, -qz соответственно, а векторная величина п принимает значения т, -I на поверхностях 2, Oj. Кроме того, по теореме Бернулли скорость на поверхности s равна qz- Следовательно, имеет место равенство

- Iqla. + mq]l = J nq4S + q\ n dS.

Так как поверхность s + Oi+Oi замкнута, то, согласно формуле (3) п. 2.20, получим соотношение

JndS=- J ndS- J ndS = I(0,-a,).

( ) (ffl) (ot)

Следовательно,

m/7j2-I(20,-0O<7j= \ nq4S.

Умножим это уравнение скалярно на I/(oi) и исключим qi с помощью уравнения неразрывности в форме qiZ - qt. Тогда если а = a,/0t-коэффициент сжатия, то мы получаем равенство

:а Е>

-5 <1У-

< !L

2-Im

Если плоскость отверстия вертикальна, то lin = 0, и знаменатель дроби в правой части равенства равен 2. Этот результат имеет место также и в том случае, когда величина 0i/2 пренебрежимо мала.

В случае истечения из отверстия в бесконечной пластинке имеем 1п -1и

2 2ai

С другой стороны, если вертикальный цилиндрический насадок, обращенный внутрь, прикреплен к отверстию в горизонтальном дне сосуда с вертикальными стенками, то на сторонах сосуда 1п = 0 и опыт показывает, что q почти равно нулю на дне. Таким образом.

в2 2

и если величина Ot/S пренебрежимо мала, то a = Vf

3.40. Скорость изменения количества движения. Рассмотрим жидкость, которая в момент времени t находится внутри (рис. 53) замкнутой поверхностях. В момент времени t-bt эта масса жидкости переместится и займет внутренность замкнутой поверхности S.

Пусть Л-область, внутренняя по отношению к поверхности S и внешняя по отношению к поверхности S, и пусть В-область, внутренняя по отношению к поверхности S и внешняя относительно поверхности S. Пусть М -количество движения жидкости к момент времени /, находящейся внутри повер.х-ности S. Тогда в момент времени t + bt количество движения той же массы жидкости равно

Рис. 53.

плюс количество движения жидкости, находящейся в области В, минус количество движения жидкости, находящейся в области А.

Последние два члена представляют собой количество движения жидкости, которое вытекает через поверхность S за время Ы.

то поток количества движения за единицу времени через границу поверхности S определяется интегралом

-J Qq(qn)dS,

здесь-qn нормальная составляющая скорости течения жидкости через элемент dS. Тензор Q(q: q) представляет собой тензор переноса количества движения, так как его скалярное произведение на вектор п равно величине Oq (qn), которая является отнесенным к единице площади количеством движения, переносимым за единицу времени через элемент поверхности dS.

Таким образом, искомая скорость изменения количества движения определяется формулой

5Qqdt-5eq(qn)dS. (1)

<v) (s)

Если использовать теорему Гаусса [формула (7) п. 2.61], затем формулу (9) п. 3.10 и, наконец, уравнение неразрывности, то из формулы (1) получим соотношение

S (ОЯ) J [(oq) m + {qV) (Qq)]dT= J [(Qq)

dx =

-S[ W+4(-+Q(Vq))]dx=Jc,fdx. (2)

Итак, полученный результат мы можем рассматривать следующим образом: скорость изменения количества движения жидкости внутри поверхности S, когда S движется вместе с жидкостью, определяется равенством

так как здесь третий интеграл обращается в нуль в силу уравнения неразрывности [см. формулу (1) п. 3.20].

3.41. Уравнение движения невязкой жидкости. Рассмотрим жидкость, которая в момент времени / занимает область, ограниченную фиксированной замкнутой поверхностью 5. Согласно второму закону движения, полная сила, действующая на массу жидкости, равна скорости изменения количества движения.

Движение жидкости происходит, во-первых, под действием нормального давления на границе и, во-вторых, под действием внешней массовой силы (такой, как сила тяжести); внешнюю массовую силу, отнесенную к единице массы, обозначим через F.

Таким образом, после применения теоремы Гаусса полная сила, действующая на жидкость, может быть записана в виде

J pndS+ J ?Qdx= - J {Vp)dx+ J FQdT.

Следовательно, скорость изменения количества движения жидкости, которая в момент времени t занимает область внутри замкнутой поверхности S, равна dNi/dt плюс поток количества движения за единицу времени через границу поверхности S.

Поскольку

Приравнивая эту величину скорости изменения количества движения, вычисленной по формуле (2) п. 3.40, находим уравнение

S(FQ-Vp-Q)dT = 0.

Так как объем, по которому происходит интегрирование, совершенно произволен, то мы можем этот объем стянуть в точку и, следовательно, получить уравнение

FQ-Vp-g = 0,

или

которое представляет собой уравнение движения жидкости.

Кроме того, из формул (9) п. З.Ю и (IV) п. 2.34 находим соотношение

= b(qV)q=l4-iv,*-qX(Vxq). Следовательно,

-j-qX(Vxq) = F-lvp-4v<? . (2)

Это соотношение представляет собой другую форму уравнения движения).

3.42. Теорема Эйлера о количестве движения. Выведем теперь общую форму теоремы, установленной в п. 1.90. Из формулы (1) п. 3.40 мы имеем следующее выражение для скорости изменения количества движения жидкости внутри замкнутой поверхности S:

§i Jgqdt- (nq)QqrfS.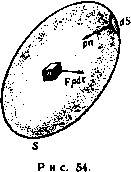

и, следовательно, применяя второй закон движения и используя рис. 54, получаем следующее уравнение:

nprfS=-С QFdT-t---5 OqdT- [(nq)eqdS.

(S) (S)

Из этого уравнения следует, что результирующее давление на жидкость, содержащуюся внутри

замкнутой поверхности S, равно сумме трех слагаемых: 1) взятой со знаком минус результирующей массовых сил, действующих на жидкость внутри поверхности 5, 2) частной производной d/dt от количества движения этой жидкости и 3) потока количества движения жидкости за единицу времени через границу поверхности S во внешнюю область. Это - обобщенная форма теоремы о количестве движения. Следовательно, ее можно рассматривать как обобщение теоремы, известной под названием €прницип Архимеда , к которой она сводится, если жидкость покоится

3.43. Консервативные силы. Для консервативных сил, т. е. имеющих потенциал Q, можно написать равенство F= - VS. Таким образом, если

М В отечественной литературе уравнение (I) обычно называется уравнением Эйлера уравнение (2) -уравнением движения в форме Громеки-Ламба. -/7рил. ред.

давление является функцией плотности так, что dp/Q существует, то из формулы (5) п. 2.31 получим соотношение

и, следовательно, так как величина dr произвольна, то

Тогда уравнение движения (1) п. 3.41 принимает форму

откуда следует, что ускорение есть градиент потенциала ускорения dp/Q + Q.

Далее, замечая, что вихрь выражается равенством S = V X q, уравнение (2) п. 3.41 можно записать в виде

qXC=-VX, x-5 + Q + l<, . (3)

где явно выделен вектор вихря.

Кроме того, формулу (1) п. 3.41 можно написать в виде

Q§ + Q(qV)q = -V/)-QVQ,

в то время как из уравнения неразрывности (4) п. 3.40 следует

q + qV(Qq)=0.

Складывая два последних равенства и используя формулу (X) п. 2.34, мы получаем уравнение

-+V[Qq;q + /pl+QVQ = 0, (4)

где / -единичный тензор.

В прямоугольной декартовой системе координат уравнение (2) эквивалентно следующей системе трех уравнений:

да , .да . dv ,да <ЭП I др .е\

Если C=iS-f )я+кС. так что %, т], Х> являются компонентами вихря, то уравнение (3) эквивалентно следующей системе: