где

f дш до ди dw у. да ди

~~д^~дг ~~дг~дх ~дх~ду

Читатель мог бы проверить, что уравнения (5) и (6) эквивалентны. Вышеуказанный результат иллюстрирует, как векторные обозначения сокращают выкладки и делают результаты легко обозримыми.

Если qx£ = 0, то течение в этом случае называется течением Бель-трами^у, соответствующее уравнение движения получается из уравнения (3) в виде

?-=-Vx. x=$f+ q-bi<7. (7)

Если вихрь отличен от нуля, то условие qxS = 0 показывает, что вихревые линии и линии тока совпадают. Если £ = 0, то мы имеем важный случай безвихревого движения, которое является также течением Бель-трами и для которого выполняется уравнение (7).

В случае несжимаемой жидкости dpiQ заменяется в вышеуказанных

уравнениях величиной plq.

Полученные выше уравнения известны как уравнения движения в форме Эйлера. В этом случае рассматривается отдельная точка г в пространстве. В течение времени / эту точку занимает последовательно непрерывный ряд частиц жидкости; величины г и / - независимые переменные.

3.44. Уравнение движения в форме Лаграижа. С точки зрения Лагранжа, вместо того чтобы рассматривать отдельную точку пространства, анализируется отдельная жидкая частица и изучается ее перемещение. Независимыми переменными являются Го -вектор начального положения частицы и время t. Если частица в момент времени / занимает положение г, то г = г(го, 0. так что ускорение частицы равно частной производной drldt, и, следовательно, используя формулу (8) п. 2.71, уравнение движения (I) п. 3.41 можно записать в виде

dt q дт Q дт дто

Умножим это уравнение на символическую диаду д; г/дго- Тогда, учитывая формулу (9) п. 2.71, получим уравнение

которое представляет собой уравнение движения в форме Лагранжа; при этом дифференцирование производится по независимым переменным Го, /*).

Если F= - ТЙ, то после интегрирования по времени от О до / получим уравнение в форме Вебера, а именно

) в отечественной литературе это течение называется винтовым. Подробное исследование таких течений было проведено в конце XIX века проф. Казанского университета Гроыеко. -Прим. ред.

*) Другой вывод этого уравнения без нспо.пьзования диад дан в приложении.- Прим. ред.

*) Это равенство легко выводится из уравнения неразрывности, см. приложение.- Прим. ред.

*) К этому же результату можно прийти другим путем. Умножая равенство (I) последовательно на единичные векторы q<> и go, получаем

VXqO= = o,

т. е. X=const вдоль линии тока; аиа.югично дХ/д^=0.-Прим. ред.

Уравнение неразрывности получается из формулы (1) п. 3.20 в виде

edT = eorfTo, (3)

где нулевой индекс относится к начальному положению частицы. Уравнение (3) выражает тот факт, что масса частицы остается неизменной во время движения.

В прямоугольных декартовых координатах справедливы равенства

dx = dxdydz, dxo - dxodyodzo

и

dxdydz = Jdxodyodzo,

где У -якобиан координат (х, у, z) вектора г относительно координат {Хо, уо, Zo) вектора Го. В этих обозначениях уравнение неразрывности принимает вид

Qj = Qo. (5)

Поверхность F(r, /) = 0 всегда состоит из одних и тех же частиц жидкости тогда и только тогда, когда d?ldt=Q). Это условие означает, что векторная функция Р(г, /) не зависит от времени и, следовательно, уравнение поверхности, выраженное в координатах Лагранжа, имеет вид /(Гв) = 0. В частности, это имеет место в случае, когда свободная поверхность жидкости находится в непрерывном движении.

Отметим, что вектор Го не обязательно должен быть вектором начального положения. С этой целью может быть использован любой переменный вектор, характеризующий положение частицы и непрерывно изменяющийся от одной частицы к другой (см., например, п. 14.80).

3.45. Установившееся движение. Если движение установившееся, то dq/dt = 0 и из уравнения (3) п. 3.43 мы получаем

qxg = ?X. X=5-f+ {<? + Q- (1)

В силу смысла символа V, примененного к скалярной величине, это уравнение показывает, что вектор qXE перпендикулярен поверхности

где с - константа. Так как вектор q X g перпендикулярен векторам q и £, то отсюда следует, что любая поверхность вида (2) содержит как линии тока, так и вихревые линии. Вдоль каждой такой линии тока или вихревой линии член, стоящий в левой части уравнения (2), имеет одно и то же постоянное значение. Уравнение (2) является общей формой уравнения

Бернулли для жидкости. Для несжимаемой жидкости интеграл J dp/Q

в формулах (1) и (2) заменяется величиной р/е').

Существование поверхности (2) является необходимым условием, для того чтобы было возможно установившееся движение.

Если движение установившееся и безвихревое (5=0), то уравнение (1) показывает, что константа в равенстве (2) имеет одно и то же значение во всей жидкости.

3.50. Уравнение энергии. Если поле массовых сил консервативно и стационарно, то уравнение движения (1) п. 3.41 после скалярного умножения на eq приводится к виду

iQ-Si(Q)= -qVp-oqVQ.

Так как dQ/dt = 0, то в силу формулы (9) п. 3.10 мы получим равенство

и, следовательно,

-J-(7 4-fll = -qVp.

Умножим это уравнение на элемент объема dx и заметим, что, согласно уравнению неразрывности [формула (1) п. 3.20, справедливо равенство

Далее, проводя интегрирование по всему объему жидкости, получим уравнение

-j[Q(iq+Q)dx=-\qVpdx.

Теперь если

7 = 54 Qqdx, V = 5 eflrft, J=QEdx

представляют собой соответственно кинетическую, потенциальную и внутреннюю (см. п. 1.60) энергии, то, используя формулу (VI) п. 2.34 и применяя теорему Гаусса, мы получим равенство

iL(r-f V)= - 5 ?(pq)dT+ 5 pVqdT: = J pqndS-b J pVqdx,

причем здесь поверхностный интеграл берется по граничной поверхности; п -единичный вектор внутренней нормали.

Теперь последний интеграл в правой части равен -dJ/dt (см. пример 31 гл. 3), и поэтому находим

(r+V + y)=5pqndS.

Эта формула выражает тот факт, что скорость изменения полной энергии любой части движущейся жидкости равна мощности давления на границу.

3.51. Скорость изменения циркуляции. Пусть С-замкнутый контур, движущийся вместе с жидкостью, т. е. контур, который всегда состоит Hi одних и тех же частиц жидкости. Пусть а обозначает ускорение частицы жидкости и В ее вихрь

а = . B = Vxa. (I)

где - число единичных В-трубок, проходящих сквозь контур С. Этот результат справедлив для потока вязкой и сжимаемой жидкости, так же как для невязкой или несжимаемой жидкости.

Для невязкой жидкости под действием консервативных сил мы имеем

а= -Vp-?q.

и, следовательно,

B = Vpxv(j). (7)

Если мы назовем величину 1/Q удельным объемом жидкости, то векторы 7р и Г(1/е) соответственно перпендикулярны поверхностям постоянного давления и постоянного удельного объема, так что вектор В касателен к кривой пересечения этих поверхностей. Направление вектора В определяет знак циркуляции по контуру С.

Рассмотрим пример. При заданных температуре и давлении вода с большим содержанием соли имеет большую плотность и, следовательно, меньший удельный объем. Предположим, что в океане содержание соли уменьшается в некотором направлении. Тогда удельный объем в том же направлении увеличивается, а давление всегда растет книзу. В результате оказывается, что циркуляционное течение вдоль дна происходит в направлении уменьшения содержания соли, а вдоль поверхности - в направлении увеличения содержания соли. Этим объясняются морские поверхностные течения в более соленое Средиземное море из Черного моря через Босфор и из Атлантики через Гибралтарский пролив.

Из формулы (6), очевидно, следует, что необходимым и достаточным условием для постоянства циркуляции по замкнутому контуру, движущемуся вместе с жидкостью, является условие V х а = О или В = 0.

Тогда в движущейся жидкости для скорости изменения циркуляции Г по замкнутому контуру С мы имеем

(С) (С) (С) (С)

так как qd(dr/d/) = qdq, то, следовательно, интеграл по контуру С от этой величины равен нулю.

Таким образом, по теореме Стокса имеем

5 adr= 5 n(Vxa)dS, (3)

(С) (8)

где интеграл в правой части берется по любой поверхности S, натянутой на контур С. Следовательно,

r\nbdS. (А)

Теперь заметим, что векторное поле В является соленоидальным (см. п. 2.24, примечание), так как, согласно уравнению (II) п. 2.32,

7В=7(Гха)=0 (5)

и, следовательно, мы можем определить единичные В-трубки (2.615). Таким образом, из уравнения (4) находим

rN, (6)

Основным следствием этого результата является теорема Кельвина о постоянстве циркуляции по замкнутому контуру, движущемуся вместе с жидкостью если жидкость является идеальной, а ее плотность или постоянна, или является функцией давления {баротропная жидкость)*).

Доказательство. Если плотность q является постоянной, то V(1/q)=0 и из формулы (7) следует В = 0. Если плотность q является функцией от р, то векторы V(l/e) и Vp параллельны между собой и, следовательно, из формулы (7) имеем в = 0. В обоих случаях d Tldt=0, так что Г не зависит от времени.

3.52. Вихревое движение. Если 5 -вектор вихря, то мы имеем

5=VXq

и, следовательно, из уравнения (II) п. 2.32 получим

Vg=0.

так что дивергенция вихря повсюду равна нулю; следовательно, вектор вихря является соленоидальным вектором.

Вихревые линии уже были определены в п. 2.41. Если через каждую точку замкнутой кривой мы проведем вихревую линию, то получим вихревую трубку.

Вихревой нитью^) называется вихревая трубка, площадь поперечного сечения которой бесконечно мала. По теореме Гаусса, примененной к объему, заключенному между двумя поперечными сечениями с площадями doi и da вихревой нити, мы получаем

j5ndS=-5vSdT = 0,

п так как ng = 0 на стенках вихревой нити, то

Sin, doi-b £20202 = О,

где 5 £2 -вихри на концах вихревой нити. Таким образом, получаем равенство

Udoi = lida2.

Оно показывает, что величина вихря, умноженная на площадь поперечного сечения, постоянна вдоль вихревой нити*).

Отсюда следует, что вихревая нить не может кончаться в точке внутри жидкости. Поэтому вихревые нити должны быть или замкнутыми (вихревые кольца), или кончаться на границах.

Можно отметить аналогию вихревой нити с соответствующим свойством нитей тока в жидкости, поскольку в случае несжимаемой жидкости Vq = 0, так что вектор q, подобно является соленоидальным вектором.

3.53. Сохраняемость вихревого движения. Если а -ускорение, то мы

dt dt qxfe-rVg-

*) То есть контур состоит из одних и тех же частиц жидкости в течение всего времени движения.- pujM. ред.

*) Автор испо.11>зует термин сбаротропная жидкость . В русской литературе принято говорить не о баротропных жидкостях, а о баротропных процессах, поскольку в ра ных условиях для одной и той же жидкости может выполняться (или не выполняться) условие баротропности.-/7pujM. ред.

) Или элементарной вихревой трубкой. -/7рил. ред.

*) Этот результат следует иепосредствеиио из свойств соленоидальных векторов, см. п. 8.615.

или

Это чисто кинематическое соотношение дает скорость изменения вектора E/Q.

Если силы консервативные и давление является функцией плотности, то, применив операцию вихря к обеим частям равенства (2) п. 3.43, получим Vxa -0. В этом случае соотношение (1) примет вид

Это уравнение получено Гельмгольцем.

Для решения этого уравнения используем обозначение д/дг для V, и, таким образом, применяя формулу (8) п. 2.71, находим уравнение

где Го-радиус-вектор частицы в момент о. как показано на рис. 46. Дифференцируя соотношение (9) п. 2.71 по t, получаем уравнение

так как dr/dt = q. Таким образом, уравнение (3) можно записать в виде

dt \Q 9 *Ч \ дг J дто

Умножим это соотношение справа на диаду д; Го/дг и снова используем формулу (9) п. 2.71. Тогда получим равенство

4(14?)=

и, следовательно,

.i=£o. = const = -. (6)

где Со и Qo -значения С и q в момент времени о-

Соотношение (6) снова умножим справа на диаду д; г/дго и используем формулу (9) п. 2.71. Тогда

lbL.L. (7)

Q во

Из формулы (6) мы видим, что если go = 0, то 5 = 0, так что если движение было безвихревым, то оно таким и остается. Следовательно, частица, имеющая вихрь в какой-либо момент времени, будет продолжать иметь вихрь. Таким образом, как вихревое, так и безвихревое движения сохраняются).

==o.

>) в приложении приведено доказательство теоремы без использования диад.-Яриж

Вычисляя вихрь и используя формулы (III) п. 2.32 и (II) п. 2.34, получаем

? X а = §-(;V) q+ (qV) 5+ S(?q)-q (Vg).

Теперь заметим, что из п. 3.52 следует ?Е = 0, а из формулы (5) п. 3.20 имеем e?q=s-de/d/. TaioiM образом, используя формулу (9) п. 3.10, находим соотношение

Заметим, что это заключение зависит от предположений, которые приводят к уравнению (2): жидкость невязкая, силы консервативные, давление является функцией плотности.

3.54. Сохраняемость вихревых линий. Если невязкая жидкость движется под действием консервативных сил и давление является функцией плотности, то вихревая линия состоит всегда из одних и тех же частиц и, следовательно, движется вместе с жидкостью.

Доказательство. Пусть линия, состоящая из частиц жидкости, определена параметром Лагранжа а, так что в момент времени t радиус-вектор частицы равен г=г(а,/). Тогда в момент / касательная к линии имеет направление вектора дг/да.

По определению вихревой линии вектор вихря касается этой линии и, таким образом, если £о -вектор вихря в момент времени to, то мы имеем

Хео = 0, или £0 = 0-. (I)

где Яо -скаляр и эти соотношения эквивалентны. Из формулы (7) п. 3.53 для момента времени / мы имеем

так что та же частица а находится все еще на вихревой линии.

Таким образом, вихревая линия движется вместе с жидкостью подобно материальной субстанции. Кроме того, эта линия не может исчезнуть, так как мы доказали, что вихревое движение сохраняется.

Отсюда следует, что если в реальной жидкости вихревая линия исчезла, то причиной этого является внутреннее трение*).

3.55. Относительное движение. Понятие скорости обычно связывается с некоторой системой координат, которую фиксирует наблюдатель. Так, например, скорость земного тела обычно вычисляется относительно системы координат, закрепленной на земном шаре.

Рассмотрим теперь две прямоугольные декартовы системы координат Охуг, или F, и О'х'у'г', или F, изображенные на рис. 55. Каждую систему координат можно отождествить с системой проволок, жестко связанных и движущихся с системой координат. Предположим, что в некоторый момент времени / системы координат совпадают и что система F движется относительно системы F; это f и с. 55.

движение описывается наблюдателем,

находящимся в системе F, как движение точки О' со скоростью U и как вращение всей системы F с угловой скоростью ш. Тогда радиус-вектор г отдельной частицы жидкости Р в момент времени / одинаков для обеих систем*).

Пусть q, q -скорости частицы жидкости Р в момент времени t, установленные наблюдателями, находящимися соответственно в системах F и F. Тогда q = q-l-U-l-(i)Xr и, следовательно, для внхря имеем соот-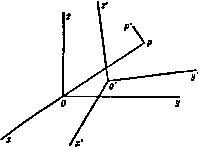

) в приложении приводится теорема Фридмана о вихревых линиях.-Прим. ред.

2) Рис. 55 показывает относительные положения систем координат в момент --д/, когда они больше не совпадают. Частица жидкости, находящаяся в момент t в точке Р, в момент времени t-\-bt будет находиться в точке Р'.

и, следовательно.

ношение

g = Vxq-Vxq4-?X(®Xr) -5 + >{Vr) -(©V)r = = ;Ч-3©-ю = ;-}-2®,

так что, подобно скорости, вихрь является понятием, связанным с системой координат. Если вихрь g = 0 в системе координат F, то наблюдатель, связанный с этой системой, утверждает, что движение безвихревое и, следовательно, имеется потенш1ал скоростей ф, такой, что qa - 7ф, в то время как наблюдатель, связанный с системой координат F, утверждает, что движение вихревое с вихрем -2а>.

Точно так же циркуляция является понятием, связанным с системой координат, так что если Г -циркуляция по замкнутому контуру С, определяемая наблюдателем, находящимся в системе координат F, и если Г' - циркуляция по тому же контуру, определяемая наблюдателем, находящимся в системе координат F, то

r=r-t-2©S.

где S -площадь, ограничиваемая проекцией контура С на плоскость, перпендикулярную вектору со.

Для доказательства заметим, что

Г-Г'= Jqrfr- 1ч'г= 5 (U-b©xr)dr = ® (rxdr).

(С) (С) (С) (С)

Положим <л = слк, тогда получим

ю \rxdr = <a {xdy-ydx) = 2<aS. <й) (С)

Эти соображения имеют значение в динамической метеорологии, изучающей движение атмосферы с учетом вращения Земли.

3.60. Безвихревое движение. Уравнение для давления. Если давление является функцией плотности p = f{Q), то уравнение безвихревого движения) под действием консервативных сил дается формулой (7) п. 3.43 и имеет

Так как скорость при безвихревом движении q=-Уф, то отсюда получим уравнение

где С (/) обозначает константу, зависящую только от времени /, которая поэтому в данный момент времени имеет одно и то же значение во всей жидкости. Оютношение (1) назовем уравнением для давления*). Функция

1) Движение безвнхрево и жидкость несжимаема.

Вдоль некой тока линии плывет форель одна. Тогда об этой рыбине уже заранее знаем мы: Чем выше сКорость жидкости - быстрей плывет она.

сЭврика , Кэмбридж. (Перевод Е. М. Дмитренко)

2) Соотношение (I) в русской литературе называется интегралом Кошн -Лагранжа. - Прим. ред.

С(/) может быть заменена абсолютной константой путем добавления к р подходящей функции от t. Добавление такой функции к ф не изменяет соотношения q = - Гф. Если движение установившееся, то d(p/dt = О и мы получим уравнение Бернулли с одинаковым значением С во всей жидкости в течение всего времени.

Уравнение для давления имеет важное значение. В самом деле, как только мы знаем потенциал скоростей ф, то скорость определяется уравнением q=-?ф и давление тогда находится из уравнения для давления и соотношения p = f(6).

Заметим, что частная производная дф/д/ вычисляется при изменении только времени / и, следовательно, относится к фиксированной точке в пространстве.

Если жидкость несжимаема, то уравнение для давления имеет вид

Отсюда вытекает, что в основном решение любой задачи безвихревого движения жидкости сводится к нахождению потенциала скоростей ф, удовлетворяющего уравнению Лапласа VV = 0 и другим условиям задачи. Расчет давления в жидкости на поверхности сводится тогда к квадратурам.

3.61. Уравнение для давления относительно подвижных осей. Рассмотрим, так же как и в п. 3.55, подвижную систему координат F, движение которой относительно мгновенного положения*) системы координат F с началом координат в точке О описывается поступательной скоростью и и угловой скоростью с . Если точка Р, радиус-вектор которой относительно точки О равен г, жестко связана с системой координат F, то она имеет скорость V = U -f ю х г.

Таким образом, если точка Р неподвижна в системе F, а не в системе F, то наблюдателю, связанному с системой F, будет казаться, что эта точка движется со скоростью-V. Если движение относительно системы F безвихревое, то существует потенциал скоростей ф, такой, что q=-Гф, и скорость изменения ф в неподвижной относительно системы F точке вычисляется набюдателем, связанным с системой F, следующим образом (ср. п. 3.10):

а- )Ф.

Следовательно, уравнение для давления жидкости принимает вид

--}--(7 -на-4Т + Ф=С(/).

Пусть qr -скорость жидкости относительно подвижной системы координат. Тогда

qr=q-V=-?ф-V.

Таким образом.

+ V(Vф)=l(q-V) -i-V*,

и. следовательно, уравнение для давления относительно подвижной системы координат может быть записано в виде

М Это мгновенное положение системы координат F считается стандартным, совпадающим с положением неподвижной системы координат, указанной в п. 3.55.

F = 1q 5 ik/MS.

Так как nq является составляющей скорости жидкости, перпендикулярной к границе, то в точках на границе nq = 0 (рис. 56). Поэтому мы можем написать равенство

F=c J[nq -2q(nq)ldS, (1)

где поверхностный интеграл берется по поверхности препятствия. Пусть S -замкнутая поверхность, целиком окружающая препятствие, и пусть п' -единичная нормаль (проведенная наружу из области между S и S) к элементу dS.

Тогда, интегрируя по поверхности S-t-S и применяя теорему Гаусса (3), (7) п. 2.61 и формулу (IV) п. 2.34, мы получаем соотношение

5 (n<? -2q(nq)]dS=- J IV / -2q(Vq)-2(qV)qldT =

<S+S) (V)

= - \ l2qX(VXq)-2q(?q)IdT.

Поскольку движение безвихревое, то ?Xq = 0. Если область между S и S не содержит источников или стоков, то из уравнения неразрывности получим Vq = 0 и, следовательно, объемный интеграл обращается в нуль. Отсюда следует равенство

5 In<? -2q(nq)IdS= j[ Щ V - 2q (nq)] dS.

(S) (S)

Таким образом, в формуле (1) мы можем заменить поверхность 5 окружающей ее некоторой другой поверхностью при условии, что не имеется никаких особенностей в жидкости, т. е. если ее можно заменить какой-либо взаимно переводимой поверхностью (см. п. 3.70).

где </г -величина скорости жидкости в точке Р относительно подвижной системы и V-скорость той же точки, которая считается неподвижной относительно подвижной системы координат.

3.62. Давление жидкости иа препятствие. Рассмотрим обтекание неподвижного препятствия S. Пусть F -сила, действующая на препятствие за счет гидродинамического давления. Пусть п -единичная внешняя нормаль

к элементу dS поверхности препятствия; тогда имеем

Р= - 5 pndS.

Кроме того, так как движение установившееся, то из уравнения для давления находим

Рис.56. р = const--0(7*.

Заметим, что постоянное давление не оказывает результирующего действия на замкнутую поверхность; следовательно, отсюда получаем