как ШИМ, делится на двухстороннюю, когда указанная точка расположена в середине интервала, и одностороннюю, когда указанная точка расположена в начале или в конце интервала.

2.1.3. ОДНОУРОВНЕВЫЕ ФОРМЫ ВЫХОДНОГО НАПРЯЖЕНИЯ

Однократная ШИМ, Прямоугольное выходное напряжение с одним импульсом в полупериоде (рис. 2.4, а) содержит нечетные гармоники с номером п, напряжение которых

= [4/(я/г)] и А sin {ynnl2) sin пШ, (2.8)

где и А - амплитуда прямоугольного напряжения; у - относительная длительность импульса прямоугольного напряжения; причем

У = иТ, (2.9)

где /и - длительность импульса; Т - период повторения импульсов.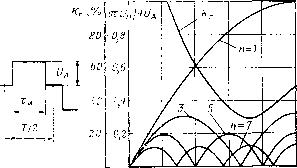

О D

0,2 0,4 05 08 у

Рис. 2.4. Однократная ШИМ одноуровневого напряжения

На рис. 2.4, б показаны построенные по (2.8) с первой по седьмую нечетные гармоники и коэффициент гармоник, определяемый по (2.1). При прямоугольном напряжении без паузы на нулевом уровне (v=l) напряжение U=Ua, а напряжение 61 = 4 ta/л;1/2 .

Поэтому коэффициент

/Сг = 100 VnVS - 1 = 48,4 %.

При введении паузы на нулевом уровне {уФ1) напряжения и = UY; и^ = (4/я 1/2) sin {уп/2) Ua.

Следовательно,

Кг = 100 l/nV8sin(n7/2)-1. (2.10)

Минимальное значение Кг соответствует длительности импульса у -0,74 (пауза 46,44), при которой Кг=29 %.

Согласно (2.8) при 7=0,66 и у=1 отношение каждой из высших гармоник к первой

UJU=\/n. (2.11)

Если подставить (2.11) в (2.5) и учесть только ближайшую к основной высшую гармонику с номером Птш, то получим приближенное значение (с точностью 5-10 %) коэффициента гармоник, %, на выходе LC-фильтра с относительной частотой со*:

/с,ф = 100 rniJ n- 1) и, = 100/(соХт- 1) mm, (2.12)

со* = ]/(100 + /с,ф/2гп) сг.Ф т.Ъ. (2.1 3)

Построенные по (2.12) для Птш = 3 и Птт = зависимости Д ,ф=/(со*) (кривые i и 2 на рис. 2.5) показывают, что параметр

фильтра со*, определяющий реактивную мощность его элементов, более чем вдвое уменьшается при введении в прямоугольное напряжение паузы

60°, когда Птгп = (у = 0,66),

и исключении тем самым третьей гармоники. При этом коэффициент гармоник на входе фильтра /(г=31,2%.

Многократная неравномерная ШИМ. Если фронты импульсов выходного напряжения формировать в определенных некратных углах (долях полупериода), подобранных так, чтобы исключить высшие гармоники низкого порядка, то получим неравномерную ШИМ, двухполярную [2.4] (рис. 2.6, а) или однополярную [2.2] (рис. 2.6,6).

При этом число исключаемых из спектра высших гармоник, ближайших к основной, соответственно равно:

искл ~ i -искл -

Следовательно, с учетом присутствия в спектре только нечетных гармоник номер наинизшей гармоники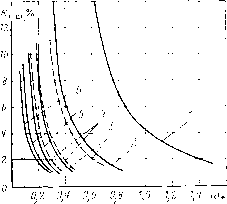

Рис. 2.5. Зависимость коэффициента гармоник выходного напряжения от о* фильтра

fmin = 2i + I ДЛЯ двухполярной ШИМ; тпгп = 2i + 3 для однополярной ШИМ.

(2.14)

при двухполярной ШИМ относительная амплитуда наинизшей из высших гармоник составляет 25-30 %, а следующей за ней - 40-50 %.

при однополярной ШИМ амплитуда наинизшей из высших гармоник составляет 18-19 %, а следуюш,ей за ней-20-25 %.

Поэтому, использовав (2.5) с учетом (2.14) и приняв UnminfUi равным 0,35 при двухполярной ШИМ и 0,2 при однополярной, получим коэффициент гармоник, %, на выходе LC-фильтра:

/С,.ф = 35/[(о^(2+ 1)-1 /(,.Ф = 20/[ (2i +3)-1

для двухполярной ШИМ; для однополярной ШИМ.

(2.15)

Z7C t

По (2.15) построены зависимости /сг.ф=/(со*) для i = 3, 5, 7, показанные на рис. 2.5 (соответственно кривые 3-5, непрерывные линии - однополярная ШИМ, штриховые- - т^-г двухполярная).

При увеличении числа импульсов примерно пропорционально уменьшается значение (О*. Однополярная ШИМ по сравнению с двухполярной обеспечивает уменьшение со* примерно в 1,5 раза.

Хотя данный метод и обеспечивает легкую фильтрацию выходного напряжения, его реализация затруднена необходимостью поддержания относительно стабильных некратных углов коммутации силовых транзисторов. Поэтому даже для выходной частоты инвертора 400 Гц изменение времени задержки выключения силовых транзисторов не должно превышать долей микросекунды, а частота задаюш,его генератора при цифровой системе управления должна составлять несколько мегагерц. При выходных частотах 50 Гц и ниже система управления инвертора с данным видом ШИМ упрош.ается, углы коммутации для двухполярной ШИМ с t = 3 равны: ai = 23,37° и 2 = 33,18°, а для однополярной приведены в табл. 2.1 [2.2].

оси

7Г

Рис. 2.6. Многократная неравномерная ШИМ одноуровневого напряжения

Таблица 2.1

В [2.5] рассматривалась неравномерная ШИМ с четырьмя импульсами в полупериоде, расположенными симметрично относительно середины полупериода (рис. 2.6, в), при которой исключаются пары низших из высших гармоник и кратные им гармоники. Например, при 1 = 42°, 2 = 36° и аи=12° исключаются 3-я, и 5-я и кратные им гармоники, а при ai = 33 3/7°, а2 = 36°, аи=18°-5-я, 7-я и кратные им гармоники. Данный вид ШИМ позволяет снизить частоту генератора тактовых импульсов до нескольких килогерц. В первом случае fTaKT = 30 fsbix, а во втором /такт = 70/вых. Кроме того, при регулировании напряжения путем уменьшения угла и спектральный состав не изменяется.

Многократная равномерная ШИМ по синусоидальной функции построения. Данный вид ШИМ широко распространен в радиотехнике, а именно в усилителях звуковой частоты, называемых усилителями класса D. Приведенные на рис. 2.2 разновидности данного класса ШИМ были исследованы В. В. Малановым [2;6], Е. И. Усышкиным [2.7] и др. Установлено, что наилучший спектральный состав в отношении исключения высших гармоник низкого порядка имеет однополярная двухсторонняя (второго рода) ШИМ. при данной ШИМ наинизшей из высших гармоник спектра, имеющей ощутимое значение (более 2%) при числе импульсов в полупериоде i>7, является гармоника с номером

/2 , =.2£-3. (2.16)

Ее относительное значение по сравнению с следующей ближайшей к ней гармоникой составляет 17-25 %. Амплитуды гармоник данного спектра более высокого порядка уменьшаются по закону, близкому к экспоненциальному. Характерной особенностью данной ШИМ является наличие небольшой 3-й гармоники, составляющей 1,85 % при f = 7, 0,9 % при i=10, 0,4 % при t=15. Поэтому относительная частота фильтра со* не должна находиться в интервале 0,25-0,4, где близок резонанс 3-й гармоники. Использовав (2.5) с учетом (2.16) и приняв f/ rnm/i =0,2, получим коэффициент гармоник на выходе LC-фильтра:

/Сг.ф = 20/fcof {2i - 3) - 1

(2.17)

Из сопоставления (2.17) с (2.15) видно, что для получения того же коэффициента /Сг.ф при равномерной синусоидальной однополярной ШИМ число импульсов в полупериоде должно быть увели-

чено на шесть по сравнению с числом импульсов при неравномерной однополярной ШИМ. При этом, если учесть присутствие 3-й гармоники, число импульсов i должно быть не менее 10 при Кг.ф = =5 % и не менее 13 при Кг.ф = 2 % (см. рис. 2.5), т. е. почти вдвое больше, чем при неравномерной ШИМ. Частота тактовых импульсов

/такт ~ gjjj

составит при выходной частоте /вых = 400 Гц соответственно 8 и 10,4 кГц, что для современных транзисторов, как правило, не создает значительных динамических потерь.

Разбивка полупериода на равные тактовые импульсные интервалы упрощает систему управления по сравнению с системой управления рассмотренной неравномерной ШИМ, несмотря на то что число импульсов должно быть удвоено для получения того же значения г.ф.

Многократная равномерная ШИМ по ступенчатой функции построения. Для упрощения системы управления и полного перевода ее на цифровые элементы вместо аналогового синусоидального эталонного напряжения следует использовать ступенчатое эталонное напряжение Uqt, аппроксимирующее синусоиду [2.8], которое сравнивается с пилообразным опорным напряжением Uon.

Напряжение гармоники с номером п такого спектра

. rgy 7(2-1) 1 . [2qip - I) + 2т-1]пл

X sin neat, (2.18)

где I - число импульсов в полупериоде; q - число импульсов на протяжении одной ступени функции построения; р-номер ступени функции построения; т-номер импульса данной ступени; у - относительная ширина импульса в середине полупериода.

Анализ спектра данного вида показывает, что так л<е, как и при синусоидальной функции построения, при q=l номер наинизшей гармоники первого всплеска частотного спектра соответствует (2.16), а число импульсов в полупериоде i должно быть выбрано более 10. В противном случае значение 3-й гармоники, имеющейся в спектре, достаточно велико (например, при i=6, 6з = 2,3 %) и относительная частота фильтра со* должна выбираться большей 0,4, чтобы избежать резонанса 3-й гармоники, а это значит, что габариты фильтра будут не меньше, чем при однократной ШИМ с 7 = 0,66, реализуемой при значительно более простой системе управления инвертора.

Число импульсов i можно увеличить двумя путями:- увеличить число ступеней функции построения при одном импульсе на ступень (<7=1) или увеличить число импульсов на каждой ступени (9>1).

При числе ступеней больше пяти и q=l (i>10) зависимость Кг.ф=!{(й*) незначительно отличается от аналогичной зависимости

4-373 49

при синусоидальной функции построения для данного числа импульсов i (/Сг.ф в 1,2-1,3 раза больше). Однако при этом достаточно сложна будет система управления. Второй путь более целесообразен, так как, приняв число ступеней равным, например, трем, можно при несложной системе управления получить хороший спектральный состав напряжения, увеличивая число импульсов на ступень q.

Например, при q = 2 и i=12 (рис. 2.7) полностью исключены 5, 7, 9-я гармоники, 3-я составляет 0,7 %, а 11-я и 13-я-12 %. Если, использовав (2.5), построить для данного спектра зависимость /Сг.ф=/(со*), то она будет расположена примерно так же, как при

Рис. 2.7. Многократная равномерная ШИМ по ступенчатой функции построения

синусоидальной ШИМ с i=10. Следовательно, упрощение формы эталонного напряжения требует для обеспечения того же качества выходного напряжения незначительного (на 20 %) увеличения числа импульсов.

Многократная равномерная ШИМ по трапецеидальной функции построения. Использование трапецеидальной функции построения, как показано в [П.2] и других работах тех же авторов, позволяет применить систему управления, выполненную целиком на цифровых элементах, тем самым уменьшить ее габаритные размеры и повысить надежность.

Этот вид ШИМ основан на методе биений, т. е. когда в системе управления используются две серии импульсов управления, частоты которых близки между собой, а полуразность этих частот соответствует частоте выходного напряжения инвертора. Анализ спектрального состава напряжения с трапецеидальной ШИМ, проведен-

ный в указанных работах, показывает, что наилучшим вариантом данной ШИМ является равномерная однополярная односторонне-симметричная ШИМ с модуляцией по одной трети полупериода в его начале и конце (рис. 2.8). Напряжение гармоники с номером п при такой ШИМ

ял

- ctg

(2.19)

2(1+1)

где i - число импульсных интервалов в полупериоде, кратное трем.

Число импульсов в полупериоде i отличается от числа импульсных интервалов, так как средняя треть полупериода не модулируется, т. е.

/ =2i73 + 1.

Анализ (2.19) показывает, что номер наинизшей из высших гармоник, определяющей всплеск частотного спектра,

m.-n = 2t-l,

а относительная амплитуда этой гармоники не превышает 20%. Третья и кратные трем гармоники равны нулю, а гармоники от 5-й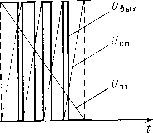

Рис. 2.8. Многократная равномерная ШИМ по трапецеидальной функции построения

ДО rimin составляют менее 5% (например, при i=12 напряжение Vb. = AA%- f/7, = 2,5%, f/ , = l,5%, f/i3, = l,4%). В связисэтим частоту фильтра со* приходится выбирать не менее 0,35. Такой фильтр обеспечивает Д'г.ф^З %, даже при числе импульсов в полупериоде i-7 (i = 9). Для получения большего /Сг.ф число импульсов может быть уменьшено до i-Ъ (t = 3). При этом для со* = 0,35 /Сг.ф 6 %. Таким образом, особенность данной ШИМ состоит в том, что ее можно реализовать с помощью цифровой системы управления с малым числом импульсов в полупериоде, а увеличение числа импульсов (в отличие от других рассмотренных выше ШИМ) не приводит к уменьшению массы и габаритных размеров фильтра. Данную ШИМ иногда называют прямой синхронизированной (ПСШИМ) в связи с тем, что в системе управления не используется эталонное напряжение, а импульсы управления формируются при смешивании прямоугольных напряжений разных частот.

2.1.4. МНОГОУРОВНЕВЫЕ ФОРМЫ ВЫХОДНОГО НАПРЯЖЕНИЯ

Формирование ступенчатого напряжения, аппроксимирующего синусоиду, осуществляется путем суммирования напряжений на секциях обмоток выходного трансформатора, на вторичных обмотках выходных трансформаторов нескольких преобразовательных ячеек, на секциях или на нескольких независимых источниках питания. При этом переменными величинами могут быть: амплитуда ступени, ширина ступени, а также одновременно и амплитуда, и ширина ступени.

Наиболее просто выполняется инвертор, когда напряжения указанных секций равны или кратны друг другу. При этом суммарное выходное напряжение получается построенным по кусочно-линейной функции, аппроксимирующей синусоиду, в частном случае по трапеции.

Трапецеидальная амплитудно-импульсная модуляция. При суммировании N прямоугольных напряжений, взаимно сдвинутых на угол ф=2я/ЗЛ, формируется напряжение с числом уровней Л^ур = = iV/2, аппроксимирующее равнобокую трапецию, длительность плоской вершины которой равна одной трети полупериода (рис. 2.9, а). Если каждое из этих прямоугольных напряжений будет иметь паузу на нулевом уровне длительностью ф/2, то число уровней Nyp результирующего напряжения удвоится, т. е. будет равно

(рис. 2.9,6).

Как видно из рис. 2.9, а, б, функция построения (трапеция) определяет высоту уровня в точках, соответствующих началам (концам) интервалов, число которых в полупериоде i=3iVyp. Высоты всех ступеней одинаковы и равны /д/А^ур, где б^д - амплитуда результирующего напряжения. Если к такому основному напряжению f/ocH добавить напряжение t/доп, имеющее форму прямоугольных импульсов с частотой, в 6Nyp раз превышающей выходную частоту, и с амплитудой, в 4Л^ур раз меньшей амплитуды выходного напряжения (рис. 2.9, б), то получим напряжение с удвоенным числом уровней, а функция построения (трапеция) будет определять высоту уровня в точке, расположенной посередине интервала.

Согласно [2.2] напряжение каждой гармоники

, J Wj, sin (мя/З) .-

- nnism{nnl2t) У - 4РУР (1 - М ( /20,

где рур - коэффициент, определяющий положение точки, в которой высота уровня равна функции построения (для формы на рис. 2.9, fl, б рур = 0, а для формы на рис. 2.9, в рур = 0,5).

Процентное содержание высших гармоник по сравнению с первой для формы на рис. 2.9, а, б

UJU = т sin {n/2i)/n sin (ппШ), (2.20)

а для формы на рис. 2.9, в

nUi =---cos(nn2t), (2 21)

Из (2.20) и (2.21) следует, что 3-я и кратные трем гармоники равны нулю, а при увеличении числа интервалов i и соответственно числа ступеней, приняв sin а я: а, получим, что отношение Un/Ui стремится к т.е. 5-я гармоника -к 4%, 7-я -к 2%, 11-я -

к 0,8 %. Кроме того, в форме на рис. 2.9, в близки к нулю гармоники с номером п, близким к (2p+l)i, где р = 0, 1, 2, 3... (независимо от i), так как cos{nn/2i) в (2.21) при этом близок к нулю. Напри-

t -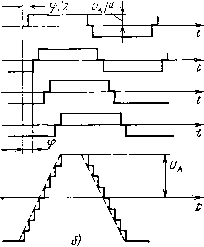

Рис. 2.9. Трапецеидальная амплитудно-импульсная модуляция

мер, в пятиступенчатой форме, показанной на рис. 2.9,6, где i=\2, близки к нулю 11-я и 13-я гармоники.

Общее содержание высших гармоник характеризуется коэффициентом гармоник Кг, который мало зависит от 3ур при данном числе интервалов i. Согласно [2.2]

К, = Ул- (10 Р - 9) tg2 (л/20/243 - 1.

(2.22)

С увеличением числа интервалов i коэффициент гармоник Кг снижается (рис. 2.10, кривая /) и при i = oo стремится к /Сг = = 4,64% (для чистой трапеции).

При рур = 0 число получаемых уровней выходного напряжения Myp = i/3, а при рур = 0,5 Nyp = i/S-\-l. Поэтому при данном числе

уровней и рур = 0 коэффициент

7 /Vyp

гармоник будет меньше, чем при формировании кривой с рур = 0,5.

Неизбежное присутствие в спектре трапецеидальной АИМ 5-й и 7-й гармоник не позволяет устанавливать на выходе инвертора LC-фильтры с малыми габаритными размерами. Однако благодаря тому, что уже при числе интервалов 1=12ч-18 коэффициент гармоник рассматриваемого напряжения составляет 8-6 %, инвертор может использоваться для непосредственного питания нагрузок, не требующих плавной синусоидальной формы выходного напряжения и имеющих активно-индуктивный характер, например электродвигателей.

Синусоидальная амплитудно-импульсная модуляция. Если для формирования ступенчатого напряжения используется синусоидальная функция построения, то в общем случае для получения минимального коэффициента гармоник могут варьироваться не только амплитуды ступеней, но и углы ступеней. Такой анализ с использованием ЭВМ был проведен в [2.9]. Его результаты приведены на рис. 2.10 (кривая 2). Такая АИМ вследствие неравенства и некратности углов ступеней трудно реализуемая и практически нецелесообразна вследствие того, что получаемый коэффициент гармоник незначительно уменьшается по сравнению с коэффициентом гармоник при равномерной синусоидальной АИМ (кривая 3 на рис. 2.10) для данного числа уровней. Кроме того, согласно исследованиям в частотном спектре появляются высшие гармоники всех номеров, начиная с третьей, что при наличии выходного фильтра может привести к ухудшению качества выходного напряжения инвертора.

Рис. 2.10. Зависимость коэффициента гармоник от числа уровней напряжения при синусоидальной АИМ