J,дg Т == ЦЯв - постоянная времени цепн ОВГ: L - индуктивность цепи; /?в - сопротивление цепи.

Учитывая, что в рассматриваемом звене (в = Хъшх, Ов = л^вх, получаем

dABbix

Т-;- + Хвых = кХвх,

где k = ХвыЦХвх = URb - коэффициент усиления.

Пример 2. Если в схеме (рис. 1.6,6) рассмотреть связь между переменными 0) н t, то, используя электромеханические свойства рассматриваемой системы прн условии пропорциональности между со и Afo - моментом сопротивления- на валу электродвигателя, можно получить

da dt

где Т = IfCi - постоянная времени; I - момент инерции, приведенный к валу двигателя; с, - коэффициент пропорциональности между Мс и со; k - kalci - коэффициент усиления; ka - коэффициент пропорциональности между моментов М, развиваемым двигателем, и током t.

Колебательное звено

Колебательным называется звено, в котором связь между выходной и входной величинами выражается уравнением

72-+2g7- + W = Bx (2.8)

при условии g < 1. в уравнении (2.8) J-постоянная времени; k - коэффициент усиления; - коэффициент затухания.

Решение линейного дифференциального уравнения (2.8), а следовательно, характер изменения д^выхСО зависит от значения корней соответствующего характеристического уравнения

W + 2lTa+\=0; (2.9)

\ ai.2 = -(i + yi-l). (2-10)

При <:1 корни 1 и 2 - комплексные. В этом случае переходный процесс в звене носит колебательный характер, а переходная функция колебательного звена имеет вид

h{t) =k Ч- sinf -barctg . ) (2.11)

Колебания (2.11) носят затухающий характер - кривая / на рис. 2.1, б. Действительно, из (2.11) при t-°° имеем д^выхСО *--

Применяя к уравнению (2.8) преобразование Лапласа при нулевых начальных условиях, получим передаточную функцию устойчивого колебательного звена:

ХвыАр) k

Если дифференциальное уравнение звена имеет вид

Т'-- Хвых = kx, (2.13)

то переходная функция

hit)=k-sinf-j4г^+arctg-j-(2.14)

Из (2.14) при t->-oo следует h{t)->-oo, т. e. колебания в таком звене носят расходящийся характер (кривая 2 на рис. 2.1, б). Звено, в котором связь между входной и выходной величинами описывается дифференциальным уравнением (2.13) при <:1, называется неустойчивым колебательным звеном.

Наконец, если в уравнении (2.8) g>l, то корни характеристического уравнения (2.9) будут вещественными:

1-1->1=-1 i-yi=-i oi = - ;-; 2 = ----

В этом случае

h{t) = ( 1 - Д e-VT.+ т.) , (2.15)

где Ту = - l/ci, Тг - - 1/а2.

Таким образом, при >1 уравнение (2.8) описывает два апериодических звена, соединенных последовательно, имеющих постоянные времени Ti и Гг и коэффициенты усиления, произведение которых равно k.

Примером колебательного звена может являться двигатель постоянного тока независимого возбуждения (рис. 1.6, б), у которого Хвх= - напряжение, подводимое к якорю электродвигателя; Хвъ1х=п - скорость вращения выходного вала, а момент сопротивления на валу Мс=0, т. е. двигатель работает вхолостую, при этом учитывается индуктивность цепи якоря. При указанных условиях уравнение двигателя

(Рп dn

Т^Т^-+Т^- + п = ku, (2.16)

где Ты - электромеханическая постоянная времени, характеризующая механическую инерцию вала; Тп - электромагнитная постоянная времени цепи якоря двигателя, характеризующая электромагнитную инерцию цепи якоря; k - коэффициент усиления.

Величины Гм, Тпяк определяются через параметры двигателя, в частности Tn=LnlRn, где Lh, Rn - индуктивность и сопротивление цепи якоря.

Обозначая в (2.16) Т^ТпТ^; 7м=2Г, получаем типовое уравнение колебательного звена, в котором Хви=и; Хвых-п:

d% dn

Уравнением типа (2.8) описывается движение массы, подвешенной на пружине, электромагнитные процессы в электрической цепи, содержащей индуктивность L, активное сопротивление R, емкость С и многие другие звенья динамических систем. Все звенья такого типа имеют передаточную функцию вида (2.12). При этом величины k я Т выражаются через конструктивные параметры соответствующего звена.

Интегрирующее звено

Интегрирующим называется звено, в котором выходная величина пропорциональна интегралу от входной величины:

л;вых = й/хвхЛ (2.17)

о

= kxx. (2.18)

Применяя к (2.17) преобразование Лапласа при нулевых начальных условиях, получим передаточную функцию интегрирующего звена:

w(p) (2.19)

На основании (2.17) имеем переходную функцию интегрирующего звена (рис. 2.1, в)

h(t) - kt.

Из (2.18) видно, что в интегрирующем звене скорость изменения выходной величины пропорциональна входной величине, т. е. интегрирующее звено является астатическим.

Примером интегрирующего звена может явиться двигатель (рис. 1.6, б) в котором в качестве входной величины рассматривается скорость вращения вала п, а в качестве выходной - угол его поворота ф. В этом случае имеем:

dip If f

n = с -jp или Ф = -J ndt = kj ndt,

где kvi с - коэффициенты пропорциональности.

Усилительное звено

Усилительным называется звено, в котором выходная величина пропорциональна входной:

W = bBx; Г(р)=-=й. (2.20)

Усилительное звено безынерционно - переходный процесс в нем отсутствует: выходная величина изменяется вместе с измене-

ниями входной величины, без сдвига во времени (рис. 2.1, г). В действительности любое реальное звено обладает инерционностью. Поэтому в динамической системе усилительным (безынерционным) принимается такое звено, в котором переходные процессы протекают несоизмеримо быстрее, чем в других звеньях системы. Примером усилительных звеньев может служить электронный усилитель в системах регулирования механических, тепловых и других инерционных процессов.

Дифференцирующее звено

Идеальным дифференцирующим называется звено, в котором выходная величина пропорциональна производной от входной величины:

W = T-, (2.21)

где X - постоянная времени звена, определяемая через его параметры.

Передаточная функция идеального дифференцирующего звена

Из (2.22) видно, что при скачкообразном изменении входной величины значение выходной величины стремится к бесконечности, т. е. при Хвх- [I]; Хвых==°° (рис. 2.1, д). Естественно, что в реальных звеньях такой переходный процесс невозможен и его описание в форме (2.21) идеализировано.

в качестве дифференцирующего звена широко применяется i?C-KOHTyp (рис. 2.1, е), для которого на основании законов Ома и Кирхгофа можно записать:

вх = Ис + iR = Uc+ вых = idt + Ывых-

Учитывая, что i=UBbix/R, имеем:

вх - ~i выхС?+ вых,

где x=RC - постоянная времени электрического контура, с. Из последнего выражения получим

X + Ивых = Т -Г^г (2.23)

Принимая во внимание, что Ывых=л:вь!х; Ubx=Xbx, на основании (2.23) запишем

т J-+ Хвъгх = т (2.24)

~ dt

Подбирая параметры звена так, чтобы х--т.-<Хвых, из (2.24)

получим уравнение идеального дифференцирующего звена -уравнение (2.21).

На выходе реальных дифференцирующих звеньев помимо составляющей, пропорциональной производной от входной величины, генерируются также другие составляющие. В линейных динамических системах наряду с идеальным дифференцирующим звеном, описываемым уравнением (2.21) и передаточной функцией (2.22), в качестве типовых структурных звеньев приняты также:

реальное дифференцирующее звено первого порядка, описываемое уравнением

(t--f л;вх) (2.25)

дифференцирующее звено второго порядка, описываемое уравнением

+ 2т:--Ьл;вх) = W- (2.26)

Применяя к (2.25) и (2.26) преобразование Лапласа при нулевых начальных условиях, получим передаточную функцию дифференцирующего звена первого порядка

и передаточную функцию дифференцирующего звена второго порядка

Р^ - (tV + 2ЬР + 1). (2.28)

Постоянная времени т и коэффициент усиления звена k определяются на основании параметров конкретных звеньев.

Дифференцирующие звенья широко используются в качестве корректирующих устройств, вводимых в систему для улучшения ее динамических свойств. С помощью таких звеньев в законы управления вводятся составляющие, пропорциональные производным по времени от отклонения или возмущения, что увеличивает быстродействие системы.

Описанными типовыми структурными звеньями охватываются все звенья, возможные в динамической системе управления. Нетрудно заметить универсальность приведенного математического описания. Действительно, описание звеньев динамических систем с использованием аппарата передаточных функций, базирующегося на исходных дифференциальных уравнениях, не зависит от их физической природы. Любая линейная система управления, независимо от назначения, структуры, физической природы ее элементов может быть представлена математической моделью в виде совокупности рассмотре|нн,ых выше типовых структурных звеньев (табл. 2.1). Это является наглядным свидетельством единства материального мира: Единство природы обнаруживается в поразительной аналогичности дифференциальных уравнений, относящих-

Таблица 2.1.

Звено

Передаточная функция

Типовое звено

Переходный процесс

Апериодическое

Колебательное

Тр + 1

к

Интегрирующее

Усилительное

Дифференцирующие

Т'р^ + 2Тр + 1

Wip) = к Wip) = TP H(p)=fc(7p+1)

к

Tp + l

->

вых = вх(1-е %

*-вых ~ -вх [1 -

±1

+ вх)

ся К разным областям явлений (Ленин В. И. Материализм и эм-пириокритицизм Соч.- 2-е изд.- Т. 14.- С. 276).

2.2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

Математическая модель линейной динамической системы может быть составлена на основе математических моделей элементов и звеньев, образующих систему. Линейная система в общем случае включает в себя звенья, соединенные последовательно, параллельно, охваченные обратными и перекрестными обратными связями. Передаточные функции всех этих структур могут выражаться через передаточные функции типовых структурных звеньев, (рис, 2.2).

Последовательное соединение звеньев. В этом соединении выходная величина предыдущего звена является входной величиной последующего звена (рис. 2.2, а). Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций всех звеньев, образующих соединение: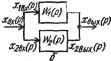

Wi(p)

We{p) 1

IVCp)

mp) fr

W,z(p)-

хвшСр) >->

Рис. 2.2. Передаточные функции линейных динамических систем

W(p) =

W,(p)x2(p)W,{p)

= Wiip)W2(p).

В общем случае

Wip)=fiWi{p), t=l,n, (2.29)

где п - число последовательно соединенных звеньев.

Параллельное соединение звеньев. В этом соединении (рис. 2.2, б) на вход всех звеньев подается одна и та же величина, а выходная величина равна сумме выходных величин отдельных звеньев. На основании рис. 2,2, б имеем:

Хвых(р) Х1вых(р) + Х2Бъж(р)

Р^ хМр) вх(р) = :

Wl{p)XiMP) + W2ip)X2Bx{p) .

Хш(р) . .

Так как Xibx = Хгшх - Хвх, то W{p) = Wi{p) + W2(p) или в общем случае при k параллельно соединенных звеньях

W(p) =i:Wk{p), i=\,k. (2.30)

Таким образом, передаточная функция соединения из параллельных звеньев равна сумме их передаточных функций.

Звено, охваченное обратной связью. Для этого соединения (рис. 2.2, в)

хЛр) =Хвх{р) ±Хо.с{р),

где знак минус - для случая отрицательной обратной связи, плюс - для положительной.

Передаточная функция соединения

или после преобразования

где знак плюс соответствует отрицательной обратной связи, а знак минус - положительной.

Общий случай соединения звеньев. Передаточная функция для общей схемы соединений звеньев (рис. 2.2, г) находится путем последовательного сворачивания отдельных частей схемы с использованием рассмотренных выше приемов нахождения эквивалентных передаточных функций. В результате для этого соединения имеем:

xs.(p) i + Wi(p)W2{p)+ w,(P) + w,{p)]

Соединения звеньев с перекрестными обратными связями. Для

этих соединений характерно наличие звеньев, охваченных непараллельными обратными связями. На рис. 2.2, д звено с передаточной функцией W2(p) охвачено непараллельно соединенными звеньями с передаточными функциями W4(p) и W5(p). Непосредственное применение сформулированных выше правил для нахождения эквивалентной передаточной функции системы в рассматриваемом случае невозможно. Однако после некоторых преобразований эти правила становятся применимыми. Преобразования не должны нарушать динамических свойств системы, с одной стороны, а с другой - должны обеспечить возможность нахождения эквивалентной передаточной функции на основе указанных правил.

Приведенное на рис. 2.2, д преобразование отвечает поставленному условию. Преобразование свелось к тому, что обратная связь в точке А разомкнута и включена в точке В. В новую связь включено звено с передаточной функцией Ws(p), что обеспечивает формирование на входе звена Wi(p) такого же сигнала, как и в исход-

ной системе. Эквивалентную передаточную функцию We(p) части системы, показанной штриховой линией, можно определить так:

l+W2(p)W3(p)W,(p)

Далее легко определяется передаточная функция всей системы.

Передаточная функция замкнутой системы. В замкнутой системе передаточная функция определяется как отношение выходной величины, преобразованной по Лапласу, к функции возмущающего воздействия, преобразованной по Лапласу при нулевых начальных условиях. Возмущающее воздействие может быть приложено к любой точке системы. Укажем общий способ нахождения передаточной функции по возмущению, независимый от точки приложения возмущения в системе (рис. 2.2, е).

Для определения передаточной функции по возмущению Fi(p) положим л;вх(р) = О и Fip) = 0. Тогда

Авых (Р) = Щ {Р) (Р) [Fr ip) Wn ip) - (p) Z ip) ЛГвых (p) ] ,

О'г

w(p) Wn{p)WAp)W,(p)

f,(p) ~ l + W{p)

где W(p) = Wi(p)W2{p)W3(p)z{p)-передаточная функция разомкнутой системы.

Рассуждая аналогично, находим

xZiip) й(Р) - выж'(р) Wl{p)W2(p)Ws{p)

Fip) 1 + w{p) хМр) i + Щр)

Полученные выражения показывают, что передаточная функция замкнутой системы по какому-либо воздействию представляет собой дробь, числитель которой равен произведению передаточных функций звеньев, включенных между выходной величиной и точкой приложения воздействия, а знаменатель - увеличенная на единицу передаточная функция разомкнутой системы.

Реакция системы на все воздействия определится как сумма реакций от каждого из воздействий:

(Fl) (2)

Хвых{р) = л:вых(р) + л:вых(р) + Л:вых (р),

,{р)Щ{р)трМр) + + Wn(P)W2(p)W3{p)Fi{p) + Wn(p)F2(p) Хьых(р) - l + W{p)

Отметим некоторые общие свойства передаточных функций линейных динамических систем, используемые при разработке и исследовании систем.

Передаточная функция любой линейной динамической системы может быть приведена к виду

Хвых(р) bop- + b,p-- + ... + br ip + Ьш К(р)

Р'~ хвх(р) ~ Оор + + ... + + Phnnn\

(2..6Z)

:где а и b - постоянные коэффициенты; К{р) = Ьор^ + bip * + -Ь bm-iP+ bm - полином числителя передаточной функции системы; Н(р) = йор' + aip -i + + Un-ip + йп - полином знаменателя передаточной функции системы.

В частных случаях полином К{р) может не содержать членов с оператором р и представлять собой произведение коэффициентов передачи звеньев, образующих систему. Например, в системе, состоящей только из колебательного звена,

К(р) = k, т. е. Ьт~1 = О, Ьт= k;

т. е. ап = I, ап-1 = 2Г, а„ 2 = Т^, а„ з = 0.

В системе, состоящей из последовательного соединения усилительного звена, дифференцирующего звена первого порядка и колебательного звена, в соответствии с (2.29) имеем:

\Р> т^р2 + 21Тр + 1 Н(р) -

где

К(р) =К(хр+ 1);. Ьт = К\ Ьш~1 = К%\ Ьт2 = 0; Н(р) = Г2р2.+ 2Гр +1; а„ = 1; а„ , = 2Г; ап-2 = Т^; Оп-з = 0.

Важнейшим свойством выражения (2.32) является условие п^т, т. е. порядок полинома Н(р) знаменателя передаточной функции выше или не ниже порядка полинома К(р) ее числителя. .Это условие вытекает из физических свойств звеньев реальных динамических систем и более глубоко будет обосновано при рассмотрении частотных характеристик линейных динамических систем в следующем параграфе.

В отдельных случаях при идеализации динамических процессов в некоторых звеньях условие tim может быть нарушено.)Например, для передаточной функции дифференцирующего звена первого порядка имеем W{p)-%p+\; К{р)-хр+\; Н(р)=0; т=\; п=0. Это обстоятельство лишь подтверждает условность и приближенность описания динамических режимов в системах управления с помощью линейных дифференциальных уравнений и передаточных фукций.

Важно подчеркнуть, что коэффициенты щ и bi передаточной функции являются вещественными числами, так как они выражаются через конкретные физические параметры элементов системы.

Из выражения (2.32) передаточной функции системы можно получить дифференциальное уравнение системы в целом как в разомкнутом, так и в замкнутом состоянии.

Уравнения разомкнутых систем. Пусть выражение (2.32) является передатрчной функцией разомкнутой системы. Тогда выражение

.вых (Р) Н(р) = Хвх (Р) к (р) (2.33)