будет представлять собой операторное уравнение разомкнутой системы (уравнение в изображениях переменных). Положив в (2.33) /- ,0, получим операторное уравнение свободного движения в^разомкнутой линейной динамической системе

(р)Я(р)=0. (2.34)

Переходя в (2.34) к оригиналам/ т. е. переходя от операторного уравнения к дифференциальному и обозначив Хвых-х, получаем дифференциальное уравнение свободного движения в разомкнутой линейной динамической системе

d-x dx

+ li + + + о - 0. (2.35)

Характеристическим уравнением, соответствующим дифференциальному уравнению (2.35), будет

Я(р) = О или аор + -\-----1- a ip + ао = 0. (2.36)

Целесообразно подчеркнуть, что если в (2.34) символ р означает комплексную переменную или символ дифференцирования лри нулевых начальных условиях, то в уравнении (2.36) символ р означает корень характеристического уравнения, соответствующего дифференциальному уравнению свободного движения в системе.

Из приведенных рассуждений следует весьма важный вывод: приравненный нулю знаменатель передаточной функции разомкнутой линейной динамической системы является характеристическим уравнением, соответствующим дифференциальному уравнению разомкнутой системы. В связи с этим многочлен Н{р)=0 называется характеристическим оператором системы.

Уравнение замкнутых систем. Пусть (2.32) является передаточной функцией разомкнутой системы. Для замкнутой системы в силу отрицательности главной обратной связи имеем х^х--х^ых, и (2.32) принимает вид Н(р)Хлых(р)\--К(рУхъых(р)- Обозначая Хъых-х, получим операторное уравнение свободного движения в замкнутой системе

1К(р)+Н{р)]х{р) =0, (2.37)

где К(р), Н(р) - соответственно числитель и знаменатель передаточной функции разомкнутой системы; х(р) - изображение координаты системы в точке ее замыкания.

На основании (2.37) можно записать характеристическое уравнение, соответствующее дифференциальному уравнению свободного движения в замкнутой системе

/С(р)+Я(р) =0. (2.38)

По уравнению (2.31), с учетом того, что Wo.c{p) == 1, передаточная функция замкнутой системы

W4P) -W{p)/[l + W(p)], (2.39)

где W(/?) ==/С(р)/Я(р)-передаточная функция разомкнутой системы.

преобразуя (2.39), найдем

На основании (2.38) и (2.40) характеристическое уравнение замкнутой системы можно записать в виде

Яз(р)=0. (2.41)

Таким образом, из (2.38) и (2.41) следует, что приравненная нулю сумма полинома числителя и полинома знаменателя передаточной функции разомкнутой системы или приравненный нулю полином знаменателя передаточной функции замкнутой системы являются характеристическим уравнением, соответствующим дифференциальному уравнению свободного движения в замкнутой системе.

Уравнение вынужденного движения в замкнутой системе, т. е. уравнение переходного процесса под влиянием возмущающего воздействия, может быть получено из передаточной функции замкнутой системы по возмущающему воздействию. Способ определения передаточной функции по возмущающему воздействию, приложенному в любой точке системы, рассмотрен выще (см. рис. 2.2, е).

2.3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

В практике анализа и синтеза линейных динамических систем управления большую роль играют частотные характеристики, отражающие свойства систем, работающих в режиме гармонических воздействий. К таким характеристикам относятся амплитудно-фазовые (АФХ) и логарифмические амплитудно-фазовые частотные характеристики (ЛАФЧХ).

Аналитическое выражение АФХ формально получается из выражения передаточной функции при чисто мнимом значении ее аргумента: р=](о. Таким образом, АФХ, т. е. W{ja), отражает отно-щение выходной величины ко входной при гармоническом воздействии на входе.

Пусть к системе с передаточной функцией W{p) приложено гармоническое входное воздействие с частотой со.

Хвх = Хвхе <*, (2.42)

где Хвх - амплитуда входного воздействия.

Если система устойчива, то собственные колебания с течением времени исчезнут и останутся лишь вынужденные движения. При этом в линейной системе на выходе установятся также гармонические колебания с той же частотой со:

Хвых = ХвыхеЛ<*+Р), (2.43)

где Хвых-амплитуда выходных колебаний; ф - угол сдвига фаз между выходными и входными колебаниями.

Взяв отношение выходной величины ко входной, на основании (2.43) и (2.42) имеем:

-= Л (со) е^ф(-) = W (/ш), (2.44)

где Л (ш) =-выхДвх - амплитуда вектора W{ja).

Для каждого зачения частоты ш возмущающего воздействия на входе выражение IF (/со) в комплексной плоскости представляется вектором, амплитуда Л (со) и фаза ф(ш) которого являются функциями частоты. С изменением частоты в диапазоне - оо<ш<;--оо конец вектора W{j(o) будет скользить по некоторой кривой, расположенной в комплексной плоскости.

Геометрическое место точек конца вектора W(/(d) на комплексной плоскости при изменении частоты в указанном диапазоне на-зыв.чется амплитудно-фазовой характеристикой (АФХ) динамической системы с передаточной функцией W{p).

Л1шем общий прием построения АФХ и проиллюстрируем его на конкретном примере. АФХ любого линейного звена или системы строится на основе их передаточных функций. Заменяя р=/(й, получим исходное выражение для АФХ:

( = Я(/Г) = (со)еМ ).. (2.45)

Далее, в выражении (2.45) нужно избавиться от мнимости в знаменателе, для чего числитель и знаменатель его умножим на выражение, сопряженное знаменателю:

IF ; л (/) K(i()HUii>)

где Я (/со) - выражение, сопряженное выражению H(j(o). Отделяя в (2.46) вещественную часть от мнимой, получим

W(/(o) =Р(ш)+/Q(co), (2.47)

где P{(j)) -полином, содержащий четные степени ш, т. е. вещественная часть выражения W{j(o); Q((o)-полином, содержащий нечетные степени со, т. е. мнимая часть выражения Wijto).

Нетрудно видеть, что Р((о) является четной функцией аргумента to, а Q((o) -нечетной, что свидетельствует о симметричности кривой W(j(ii) относительно вещественной оси. Поэтому, построив АФХ в диапазоне частот О < со < -foo, вторую часть АФХ, т. е. часть в диапазоне - оо <; со < О, получим как зеркальное отображение первой ее части относительно вещественной оси.

Рассмотрим построение АФХ на примере колебательного звена.

В выражении передаточной функции колебательного звена (2.12) при коэффициенте усиления k- 1

(Р) ppi + 2lTp+ 1 положим р=/о) и, принимая во внимание, что р=-1, получим

Рис. 2.3. Амплитудно-фазовые характеристики: a - колебательного звена; б - астатической системы

Умножая числитель и знаменатель последнего уравнения на выражение, сопряженное знаменателю, и отделяя вещественную часть от мнимой, получим

1 - Рш2 2(оГ

где Р (ш) = -

(1 - Г2(02)2 -f (2(0Г)2 -(1 - Г2щ2)Р -f (2(оГ)2

.= P(tt)+/Q((o), (2.47)

1 - Г2ш2

(1 Г2со)2+(2соГ) -вещественная часть; Q((o) =

2g(or

~ (l rw)2-}- (2g(o 7y--коэффициент при мнимой части.

Построенная по уравнению (2.47) АФХ колебательного звена приведена на рис. 2.3, а. Из этого рисунка видно, что для любого звена

Л(со) =y[P((o)]24-[Q(fo)];

ф((о) = arctg-

Р(со) -

Учитывая (2.48) и (2.57), для колебательного звена находим: А (ш) =- = -

(2.48)

2Гсо

ф(со) =-arctg 1 г2д2 =

Модуль АФХ представляет собой отнощение амплитуды колебаний выходной величины звена или системы к амплитуде гармонических колебаний с частотой со на входе, а аргумент вектора

АФХ равен углу сдвига фаз между выходной и входной величи-

равнения (2.45) и (2.48) являются исходными для построения АФХ любой системы с передаточной функцией W{p). Величины Р(а) и Q(cu) определяются в порядке, описанном выше.

Отметим особенность АФХ астатических систем (рис. 2.3, б), вытекаюшую из наличия в этих системах интегрирующих звеньев, вследствие чего передаточная функция таких систем имеет вид

W{p)K{p)/[p-H{p)], (2.49)

где V - порядок астатизма.

Из (2.49) видно, что при р=/(о и (о->-0 модуль вектора АФХ астатической системы стремится к бесконечности.

S Логарифмической амплитудно-частотной характеристикой (ЛАЧХ) звена или системы называется построенная в логарифмическом масштабе частот функция вида

L(tu) = 20\gA{a), (2.50)

где Л ((о)-модуль АФХ звена или системы, определяемый согласно выражению (2.48). Функция L((o) измеряется в децибеллах (дБ). С учетом физического смысла модуля Л (со) следует, что 1 дБ представляет собой 20 десятичных логарифмов отношения амплитуды выходной величины звена или системы к амплитуде входной величины.

Функция ф((о), определяемая выражением (2.48) и построенная в логарифмическом масштабе частот, называется логарифмической фазочастотной характеристикой (ЛФЧХ).

Построенные на одном графике характеристики L((o) и ф((о) представляют собой ЛАФЧХ.

Использование ЛАФЧХ позволяет легко и быстро оценить динамические свойства автоматических систем и выбрать необходимые дополнительные звенья, введение которых в систему обеспечит требуемые свойства. Упрощенными методами можно без каких-либо затруднений построить эти характеристики как для отдельных звеньев, так и для системы в целом.

Непосредственное использование выражений (2.48) и (2.50) для построения ЛАФЧХ приводит к громоздким и трудоемким расчетам. Однако при вполне приемлемых допущениях можно существенно сократить объем работы по построению ЛАФЧХ с достаточной для инженерной практики точностью. Рассмотрим приближенные методы построения ЛАФЧХ типовых структурных звеньев и линейных динамических систем, состоящих из этих звеньев.

Апериодическое звено

Используя выражение передаточной функции апериодического звена (2.3), уравнения (2.48) и изложенный выше порядок построения АФХ, найдем при k= I

Л (ш) =- ф(со) = -arctg(tur). (2.51)

Далее, на основании (2.50) получим выражение ЛАФЧХ апериодического звена:

L (со) = -20 Ig yi + ш^Г. (2.52)

Условие k~\, не имея принципиального значения при описании порядка посторения ЛАФЧХ, упрощает рассуждения.

Из анализа (2.52) видно, что при ш<С l/r выражение ш^Рл;0, следовательно, Z,(cu)=0. При ш 1/7 функция L(tu)==-2ЫgoT. Для некоторой частоты со1>1/Г имеем L((Oi)=-201gtui7.

Увеличим частоту в 10 раз, т. е. примем шг- Ю coi (заметим, что увеличение частоты в 10 раз называется возрастанием частоты на декаду). Тогда L(cu2) = -20Ig lOaJ -20Ig(0ir-20 = L(tui) - - 20. Рассуждая аналогично, для соз = lOOcoj получим Ь{(аз) = --Z.((oi) -40.

Таким образом, при увеличении частоты на декаду характеристика L(tu) апериодического звена убывает на 20 дБ. В результате порядок построения ЛАФХЧ апериодического звена сводится к следующему: левее частоты (а=1/Т характеристика L(tu) совпадает с осью абсцисс, а правее этой частоты Z-(tu) представляет собой прямую линию с наклоном - 20 дБ/дек. (рис. 2.4, а). Частота (о=1/Г=Шс, при которой характеристика /-(со) изменяет свой наклон, называется сопрягающей частотой. На рисунке по оси абсцисс отложены в логарифмическом масштабе значения частот в относительных единицах, причем за базовую частоту принята частота сос- Иначе говоря, на оси абсцисс в логарифмическом масштабе откладываются значения частот, поделенные на Wc. Крайняя левая граница рисунка (положение оси ординат функции L(cu)) определяется диапазоном частот, в котором рассматривается динамика звена.

Оценим максимальную погрешность, которая вносится при построении характеристики L(tu) апериодического звена описанным способом. Очевидно, что максимальная погрешность наступает при ш-(Ос-1/7 . В соответствий с (2.52) для этой частоты L(tu) = =-3 дБ, а в случае приближенного построения для этой частоты L(tu)=0 Насколько допустима такая ошибка, можно судить по результатам анализа каждой конкретной системы. При необходимости в приближенные расчеты функции L((o) можно внести уточнения в районе частот, прилегающих к сопрягающей частоте.

Логарифмическая фазочастотная характеристика апериодического звена ф(сй) строится по выражению (2.51), из которого следует, что ф(ш)~0 при ш->-0; ф(й)-(-90°) при ш-оо; <p((Oc) = =-arctg-1=-45° при oj = tuc=l/7. Таким образом, характеристика апериодического звена представляет собой кососимметричную кривую относительно ординаты со == Шс и абсциссы ф((о) = -45°, изменяясь в диапазоне от О до --90°.

Построение характеристики ф(ш) существенно упрощается, если применять номограмму (рис. 2.4, б), на которой снизу в логарифмическом масштабе нанесены значения ш/(0с= 7, а сверху - определенные по выражению (2.51) фазовые сдвиги в градусах, соответствующие значениям отношений со/шс. Расположив нижнюю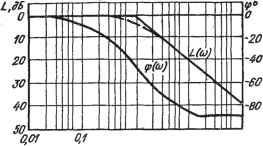

0,S 1 I-u.

3S 45 55 6 810 15S02530 40 50 60 70 . . I I I I I I I I I 1 1

85 87 88

L l 1 1

89 -i-

~S0 100

0,01 0,02 OftS 0,1 0,2 0,5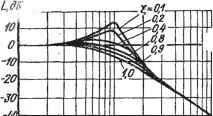

1 Z ff

S 10 20

Wtgk

01 0.2 0;} 0,50.8 1 2 3 4 6810

0,2 0,4 0.6.

-20 -60

-too

-140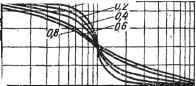

L,dE

0.2 0,30,1/0,60.81

г

2 3 4 6 810 wT

10 0 -10 -20 JO 40

30 0

30 20

10 0

-30 -10

-60 -20

-90 -30

r120 -40,

9(6))

-80 -ISO -240

Рис. 2.4. Логарифмические амплитудно-фазовые частотные характеристики: а - апериодического звена; б - номогрзмма для определения фазовой характеристики апериодического звена: в - ЛАЧХ - колебательного звена; г -ЛФЧХ колебательного звена; а -ЛАФЧХ интегрирующего звена; е - усилительного звена; ж - разомкнутой системы

шкалу номограммы на характеристике L(tu) так, чтобы отметка со/шс=1 совпала с частотой сопряжения, сдвиг фазы при любой другой частоте определяют по верхней шкале над этим значением частоты. Непременным условием применения номограммы является одинаковость масштабов номограммы и оси абсцисс характеристики L((o). Построение ЛАФЧХ звеньев и систем существенно упрощается при выборе такого масштаба по оси частот, при котором одна декада соответствует десяти сантиметрам. В таком случае логарифмы частот легко определяются по нижней шкале логарифмической линейки.

Колебательное звено

Аналитическое выражение ЛАЧХ колебательного звена получим на основании уравнений (2.47), (2.48):

L (со) = -20 Ig У(1 -r2(o2)2-f (2шГ)2. (2.53)

При (о<1/Г функция L(tu)a:;0; при функция L((o) ;

л;-20Igco272.

Проведя рассуждения, аналогичные тем, что имели место при определении формы L(tu) апериодического звена, получим следующую форму ЛАЧХ колебательного звена (рис. 2.4, в): в районе ш-С1/7 характеристика L(cu) совпадает с осью абсцисс; в районе (О > 1/Г она представляет собой прямую линию с наклоном- 40 дБ/дек. В отличие от апериодического звена, погрешность построения, характеристики Z-(tu) колебательного звена при со=(Ос= = 1/Г может быть значительной. Она не превышает 3 дБ при условии 0,3810,7. При других значениях коэффициента колебательности I характеристику L((o) в районе частоты среза необходимо строить непосредственно по выражению (2.53) или пользоваться соответствующей таблицей поправок.

Фазовая характеристика колебательного звена строится на основании выражения, вытекающего из уравнений (2.47) и (2.48):

Q((o) 2grco

ф (со) = -arctg = -arctg д ь (2.54)

Характеристика ф(ш) (рис. 2.4, г) представляет собой кососимметричную кривую относительно осей ш -сос, ф((о)=90°.

Интегрирующее звено

Для получения выражения ЛАФЧХ интегрирующего звена в уравнении его передаточной функции W{p) = \lp положим p=j(j), избавимся от мнимости в знаменателе и, используя выражения (2.48), найдем

Л (ш) - - 1/(о; ф((о) - arctg (-оо) = -л/2. (2.55) На основании (2.50)

i (со) = 20 Ig Л (со) = -20 Ig со.

Из этого выражения видно, что L(cu)=20 дБ при ..=0,1; L(cu) = =0присй = 1;.( >)==-20 дБ при ©=10.

Таким образом, ЛАЧХ интегрирующего звена представляет собой линию с наклоном - 20 дБ/дек., пересекающую ось абсцисс в; точке сй=1 (рис. 2.4, д). Как видно из (2.55), фазовая характеристика интегрирующего звена представляет собой прямую линию параллельную оси абсцисс со значением угла (р(сй)=-90°, т. е. сдвиг фазы выходной величины по отношению к входной в интегрирующем звене не зависит от частоты и равен -90°.

Усилительное звено

В уравнении передаточной функции усилительного звена: Wip)=k, положив р==](и, получим W{jbi)=k; P(cu)=fe; Q(cu)=0,.

тогда

А УР2( ) +Q(co) = k; L (ш) = 20 Ig (ш) = 20 Ig k;

(2.56)

Q((o)

cp(co) =arctg- = 0°., (2.57).

Из (2.56) и (2.57) следует, что ЛАЧХ усилительного звена представляет собой прямую линию, проходягцую на высоте 20 Ig k: (рис. 2.4, е), а ЛФЧХ - прямая, совпадающая с осью абсцисс.

Дифференцирующее звено

Исходя из уравнений передаточных функций идеального дифференцирующего звена (2.22), дифференцирующего звена первого порядка (2.27) и второго порядка (2.28) и проведя рассуждения аналогичные вышеприведенным, можно прийти к выводу, что-ЛАФЧХ идеального дифференцирующего звена является зеркальным отображением ЛАФЧХ интегрирующего звена, ЛАФЧХ дифференцирующего звена первого порядка - апериодического звена, а ЛАФЧХ дифференцирующего звена второго порядка - колебательного звена. Таким образом, например, ЛАЧХ дифференцирующего звена первого порядка до частоты cu=cuc/t совпадает с осью частот, а при а=1/т представляет собой прямую линию, проходящую с наклоном 4-20 дБ/дек. ЛФЧХ этого звена представляет собой линию, кососимметричную относительно оси ординат сй==1/т и оси абсцисс ф(сй) =45°.

Одноконтурные разомкнутые системы

Для построения ЛАФЧХ разомкнутой системы целесообразно систему представить в виде совокупности типовых структурных: звеньев. Тогда характеристики Z,(cu) и (р(сй) системы можно получить, суммируя ординаты соответствующих характеристик, построенных для каждого типового звена, входящего в систему. На практике это построение еще более упрощается и не требует построения характеристик отдельных звеньев во всем диапазоне час-

тот. Рассмотрим характерный пример, раскрывающий приемы построения ЛАФЧХ одноконтурных линейных динамических систем.

Пример. Построим характеристики L((o) и ф((й) одноконтурной системы, имеющей передаточную функцию

k 24

W(p) = .---- =-. (2.58)

К^+Тф){\+Т^р)р (1--0,07р)(1--0,28р)р

Как видно из (2.58), система включает в себя усилительное звено с коэффициентом усиления k = 24, два апериодических звена с .юстояннымн времени Ti = 0,07 с и Гг = 0,28 с и одно интегрирующее звено.

Для построения характеристики L((o) системы найдем сопрягающие частоты:

(Ос1= 1/Т= 1/0,07= 14 с-

Шс2 = 1/Т = 1/0,28 = 3,75 с-.

Само построение удобно начинать с характеристик интегрирующих звеньев (или дифференцирующих идеальных, если такие имеются в системе). С этой целью на высоте 20 Ig fe = 20 Ig 24 = 27,6 дБ при (о = 1 (Ig (о = 0) проведем линию с наклоном -20 дБ/дек., отражающую ЛАЧХ выражения kjp = 24/р (рис. 2.4, ж). Эта линия до пересечения с ординатой (0с2=3,57, с- является характеристикой L((o) всей системы, так как на этом участке частот логарифмические амплитудно-частотные характеристики апериодических звеньев совпадают с осью абсцисс и их ординаты равны нулю.

При частотах (0с2 < ш < Wci на характеристику Z.((o), отражающую передаточную функцию МР{р) = 241р, накладывается ЛАЧХ апериодического звена с постоянной времени Т2 = 0,28 с и сопрягающей частоты (Осг == 3,57 с~. Следовательно, на этом участке характеристика L(w) системы будет иметь наклон -40 дБ/дек. Продолжая рассуждения, придем к выводу, что при (о > (Ось т. е. при ш > 14,3 с~, характеристика L((o) имеет наклон - 60 дБ/дек.

Рассмотренный прием построения ЛАЧХ одноконтурной разомкнутой системы является универсальным и удобным для построения характеристики L{w) любой одноконтурной системы, представленной в виде последовательного соедн-нення типовых структурных звеньев. Как видно, этот прием сводится к тому, что сначала проводится участок ЛАЧХ, соответствующий интегрирующим (или идеальным дифференцирующим) звеньям с учетом коэффициента усиления, а далее наклон характеристики изменяется при каждой из сопрягающих частот, а именно: увеличивается на 20 дБ/дек. в апериодическом звене, увеличивается на 40 дБ/дек. в колебательном звене, уменьшается на 20 дБ/дек. в дифференцирующем звене первого порядка и уменьшается на 40 дБ/дек. в дифференцирующем звене второго порядка.

Для построения фазовых характеристик одноконтурных систем удобно пользоваться номограммой (рис. 2.4,6). По ней определяются значения фазовых сдвигов для каждого звена, а фазовые сдвиги системы находятся как сумма значений фазовых углов отдельных звеньев. Хотя номограмма построена для

Таблица 2.2