г^ппрпелення фазовых сдвигов в апериодическом звене, она может использовать-я пля построения характеристики ф((о) любого звена. При этом для колеба-трпьного звена значения фазовых сдвигов, полученных из номограммы, нужно vflBOHTb Фазовый угол для дифференцирующего звена первого порядка будет по величине такой же, как и для апериодического звена, но с обратным знаком Гплюс) а для дифференцирующего звена второго порядка такой же, как и для колебательного звена, но с обратным знаком (плюс). Напомним, что в усилительных, интегрирующих и идеальных дифференцирующих звеньях фазовые сдвиги имеют постоянные значения н не зависят от частоты: в усилительном звене ф(ш) = О- в интегрирующем ф(ш) = -90°; в идеальном дифференцирующем Ф(ш) = 90°.

В табл. 2.2 занесены числовые значения фазовых сдвигов в рассматриваемой одноконтурной системе, определенные с помощью номограммы, а результирующая характеристика (pi( ) системы приведена на рис. 2.4, ж.

Замкнутые системы

Дркамические свойства замкнутых линейных систем в значительной мере определяются с помощью ЛАФЧХ разомкнутых систем.. ieM не менее при анализе замкнутых многоконтурных систем возникает необходимость построения логарифмических амплитудно-частотной 1з(сй) и фазочастотной (рз(к>) характеристик.

Характеристики Ьз(а>) и (рз(сй) могут быть определены по соответствующим характеристикам Z,(cu) и (р(сй) разомкнутого контура. Действительно, если разомкнутая система имеет Передаточную функцию W{p), то соответствующая замкнутая система будет иметь передаточную функцию

а выражение для амплитудно-фазовой характеристики замкнутой системы имеет вид

у4((о)езФИ

As (ю) езч-зС ) =-~-

1 --Л(ш)езФ(<.>)

Из последнего уравнения, используя свойства показательных функций, можно получить

/1(со) =

yi-2[Лз(ш)]-со5фз(ш) + Из((о)]-2

8Шф4(0)

ф(сй) = arctg------7---

COS фз((0) - Лз((0)

На основании этих выражений могут быть построены так называемые номограммы замыканий (рис. 2.5), с помощью которых легко найти характеристики Ьз(а>) и срз(сй) по характеристикам Z,(cu). и ф(сй) разомкнутой системы. На номограмме в координатных осях (cu)=201gy4(cu) и ф(сй) нанесены линии равных значений Аз{(а) при переменном значении фз(сй) и линии равных значений фз(сй) при переменном значении Аз{а). На кривых приведены значения фазы и модуля. Зная значения Z,(cu) и ф(ю) при заданном значении частоты и нанеся точку с этими координатами на номограмму, можно найти значения 1,з(сй) и.фз(сй).

-J60-s20-2eo-240-f80 -120оЛ I охваченного обрат-f Зб\ I I III I II II НОИ связью, приближенно можно

выразить через ЛАЧХ обратной связи. Действительно, АФХ такого соединения имеет вид

yi ) - 1-ь W,(/(0)W .c(y(0)

где UiOco)-АФХ прямого звена; 10. с (/со)-АФХ звена обратной связи.

Если 1Г,(/ю)1Го.с(/сй) 1, то 1?(/сй) l/[lio.c(/cu)], следовательно, для этих условий

Z,(cu) = -Lo.c(cu),

т. е. ЛАЧХ звена, охваченного обратной связью, может быть замещена ЛАЧХ обратной связи, взятой с обратным знаком.

В тех случаях, когда постоянные времени структурных звеньев в системе существенно отличаются, например на порядок, сопрягающие частоты можно приближенно определить по отнощению коэффициентов передаточной функции. Не останавливаясь на обосновании этого метода построения ЛАЧХ, укажем порядок построения характеристик Z-(cu) и ср(сй) на базе отнощений коэффициентов передаточной функции многоконтурной системы.

Для использования коэффициентного метода передаточную функцию статической системы целесообразно представить в виде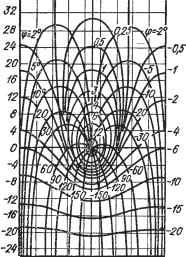

-m-m-foo-80-20020 so т т т

Рис. 2.5. Номограммы замыкания (у° - избыток фазы)

k = k

Ьтр^ + bm-lP - -I-----\-bip+\

flnp + dn-ip -* -I-----\-aip + \

(2.59)

a передаточную функцию астатической системы - в виде

k К(р) k bmP + bm-iP - -I-----1- blP -Ы

Wip) =

pv Я(р)

pv CnP + fln-ip - -I-----1- OlP -b 1

(2.60)

где V - порядок астатизма.

Введем определения. Сопрягающие частоты числителя и знаменателя Юз выразим так:

CU41 = l/6i; ©42 = 61/62; Ючт = bmi/bm;

©31 = l/Ob CU32 = ai/a2; СОзп = dn-ilO-n-

с учетом принятых допущений и определений ЛАЧХ статической системы строится следующим образом. В координатной системе Х(сй) - Ig о на оси частот отложим значения Юч и соз в порядке их возрастания. Далее, на высоте 20 Ig k проведем прямую, парал-

лельную оси абсцисс до пересечения с ординатой первой сопрягающей частоты. Если эта частота определена как соз, то наклон характеристики L(cu) увеличивается на 20 дБ/дек., если частота определена как Юч, то наклон уменьшается на 20 дБ/дек., что отражает влияние звеньев с отставанием выходного сигнала по фазе (апериодических и колебательных) и звеньев с положительным сдвигом выходного сигнала (дифференцирующих).

Для астатических систем порядок построения Z,(cu) отличается тем, что первый участок характеристики проводится через точку с координатами 20 Ig, to = 1 с наклоном - 20 v дБ/дек. Далее ЛАЧХ строится так же, как и для статических систем.

Для построения фазовой характеристики можно использовать номограмму (рис. 2.4, с) при условии, что фазовые сдвиги, определяемые сопрягающими частотами знаменателя, берутся с отрицательными знаками, а фазовые сдвиги, определяемые сопрягающими частотами числителя, - с положительными знаками. При определении суммарных значений ф(сй) необходимо учитывать фазовые с:. интегрирующих (-90°) и идеальных дифференцирующих (4-90°) звеньев, если таковые имеются в системе.

Использование ЛАФЧХ для анализа линейных динамических систем рассмотрено в последующих главах.

2.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

Важнейшей задачей анализа динамических систем является решение вопроса об их устойчивости, т. е. наличия или отсутствия в системе способности возвращаться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями. Ранее отмечалось, что неустойчивая система неработоспособна, так как любое воздействие на такую систему вызывает недопустимое возрастание физических величин, характеризующих работу системы (токи, электрические напряжения, ускорения, механические напряжения и т. д.).

Возникновение неустойчивых (расходящихся) колебаний в системе можно объяснить, например, проследив включение системы управления величиной Хвых (см. рис. 1.2, б). Управляющая величина на входе регулятора Хр в режиме установившейся работы системы определяется как разность Хр=Хвх-Хо-.с- В первый момент включения системы в силу инерционности обратной связи Хо.с^О, следовательно, Хр=Хвх, т. е. Хр Хр.уст, где Хр.уст - управляющее воздействие на входе регулятора. Естественно, что это может вызвать значительное возрастание выходной величины Хвых л;вых.уст, которая будет возрастать до тех пор, пока сигнал обратной связи не уменьшит значения Хр. Однако значительно возросшая величина дгвых через ОС передается на вход системы и существенно уменьшит значение Хр, что может привести к последующему снижению величины Хвых и возникновению условия Хвых<Сл:вых.уст. При неблагоприятном соотношении параметров системы описанные колебательные процессы могут стать расходящимися.

3 260 65

Задача исследования систем на устойчивость может быть поставлена двояко: 1) устойчива ли система при заданном значении ее параметров; 2) в каких диапазонах можно изменять параметры системы, не нарушая ее устойчивости. Вторая постановка задачи об устойчивости имеет место при наладке и эксплуатации систем автоматического управления.

Анализ систем на устойчивость и выбор средств для стабилизации неустойчивых систем осуществляются с использованием критериев (признаков) утойчивости, которые формулируются исходя из общих условий устойчивости.

Вопрос об устойчивости системы сводится к выяснению устойчивости свободного движения системы и требует анализа характера решения уравнения свободного движения, составленного относительно отклонения выходой величины х от установившегося состояния. На основании (2.35) и (2.37) уравнение свободного движения системы может быть приведено к виду

dx d-x dx

> + + - + + = (2->

где п - порядок уравнения системы; щ - коэффициенты, определяемые из параметров системы.

Линейное однородное дифференциальное уравнение (2.61) имеет общее решение вида

х= c,e + С2е' + - + Сге , (2.62)

где Си Сг, Сп - постоянные интегрирования; pi, pi, рп - корни характеристического уравнения.

Характеристическое уравнение, соответствующее дифференциальному уравнению (2.61), имеет вид К{р)-{-Н(р) - О, где К{р)у Н{р) -характеристические полиномы соответственно числителя и знаменателя передаточной функции разомкнутой системы.

Если анализируется устойчивость разомкнутой системы, то, как следует из (2.36), характеристическое уравнение имеет вид Я(р)=0. Чаще приходится анализировать устойчивость замкнутой системы.

Во всех случаях характеристическое уравнение свободного движения приводится к виду

аоР + Ч-----Ь СгР - + - + an-ip + с„ = 0. (2.63)

Корни уравнения (2.63) могут быть либо вещественными, либо комплексными попарно сопряженными.

В случае вещественных корней обозначим Pi=%,i. Тогда общее решение уравнения (2.61) представляется как сумма п решений вида Хг = Сге^ . Так как в (2.61) величина х означает отклонение регулируемой величины от установившегося состояния, то очевидное условие устойчивости при t-oo имеет вид x{t)-0. Каждая составляющая общего решения стремится к нулю лишь при отрицательном значении вещественного корня, т. е. при Лг<0.

Комплексные корни имеют вид

Pk = a,k± hk,

вещественная часть комлексного корня: ю - коэффи-

ниен/при мнимой части - угловая частота колебания.

Каждому корню ph в рассматриваемом случае будет соответствовать частное решение

Xh = Xk sin {bikt + Щ), (2.64)

где Хь=-вье * - амплитуда составляющей Xh; В^, щ - постоянные интегрирования.

Движение, описываемое уравнением (2.64), будет сходящимся, если при t-°° решение Xk(t)-*-G. Это возможно лишь при отрицательном значении вещественной части комплексного корня.

Исходя из изложенного, можно вывести условие устойчивости линейных динамических систем: линейная система будет устойчива, если все вещественные корни и все вещественные части комплексных корней характеристического уравнения, соответствующего исходному дифференциальному уравнению свободного движе-Tji истемы, будут отрицательными.

Весьма важной для практического анализа устойчивости является геометрическая интерпретация условий устойчивости. Она сводится к тому, что в устойчивой линейной системе все корни харак-- теристического уравнения, соответствующего дифференциальному уравнению свободного движения системы, на комплексной плоскости в координатах а -- /со должны располагаться слева от мнимой оси. Такие корни впредь будем называть левыми . Следовательно, условие устойчивости в такой постановке сводится к тому, чтобы корни характеристического уравнения были только левыми. Исходя из этого-, в теории управления разработан ряд признаков - критериев устойчивости линейных динамических систем, которые позволяют вынести суждения об устойчивости системы, не вычисляя значения корней характеристического уравнения. В практике исследования линейных систем автоматического управления широко используются две группы критериев устойчивости - алгебраические и частотные. Применение того или иного критерия определяется условием конкретной задачи, например порядком дифференциального уравнения свободного движения системы, наличием или Отсутствием тех или иных характеристик исследуемой системы - передаточных функций, АФХ, ЛАФЧХ и др.

Не останавливаясь на доказательствах, которые построены на утверждении необходимости левых корней для обеспечения устойчивости линейной динамической системы, приведем некоторые из критериев устойчивости.

Критерий Рауса. Практическое использование алгебраического критерия Рауса сводится к тому, что на базе значений коэффициентов характеристического уравнения (2.63) составляется таблица Рауса (табл. 2.3), коэффициенты которой bVe назовем элементами таблицы Рауса, где г - номер строки таблицы; е -номер столбца.

Элементы первой строки таблицы являются коэффициентами характеристического уравнения (2.63) с четными индексами, т. е.

Х 2~2 и т. д. Элементы второй строки представляют собой коэффициенты уравнения (2.63) с нечетными индексами, т. е. bzb=

Таблица 2.3

Ai = аи

азСгС] 050403

= Oi; 622=3 и т. д. Для нахождения остальных элементов таблицы Рауса можно воспользоваться выражением

br-l, lbr-2, e + l - br-2, ibr-i, e + l

bre = -Г-

br-i, 1

Критерий Рауса формулируется так: линейная динамическая система будет устойчивой, если все элементы первого столбца таблицы Рауса положительны. Форма критерия Рауса позволяет легко реализовать его с помощью цифровых ЭВМ. Однако этот критерий неудобен для анализа влияния отдельных параметров на устойчивость системы.

Критерий Гурвица. Для анализа устойчивости линейной системы по критерию Гурвица из коэффициентов характеристического уравнения (2.63) составляются определители Гурвица:

OiOoOO О3О2О1О О5О4О3О2 07060504

Число определителей Гурвица равно порядку характеристического уравнения п.

По критерию Гурвица линейная динамическая система будет устойчивой, если все коэффициенты характеристического уравнения и все определители Гурвица положительны.

Любой определитель Aj составляется по одному общему правилу: число строк и столбцов определителя Aj равно i; по диагонали определителя располагаются подряд коэффициенты характеристического уравнения от Oj до ас, влево от диагонали на каждой строке располагаются коэффициенты с возрастающими индексами, вправо - с убывающими. Элементы, располагающиеся вправо от Оо, и элементы с индексами, превышающими степень характеристического уравнения, заменяются нулями.

Из критерия Гурвица следуют простые алгебраические выражения, составленные из коэффициентов характеристического уравнения, удобные для анализа устойчивости систем невысокого порядка. Так, для систем первого и второго порядков достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения. Для систем более высокого порядка это условие сохраняется, но, кроме того, необходимо выполнение следующих соотношений:

в системах третьего порядка с,С2 - Соаз>0; в системах четвертого порядка ( [Ог-ОоСз) 3-0204 > 0. Недостаток критерия Гурвица - громоздкость вычислений определителей для систем высокого порядка.

Частотный критерий устойчивости - критерий Михайлова

Частотные критерии базируются на свойствах частотных характеристик устойчивых систем. Большую роль в развитии теории устойчивости сыграл частотный критерий устойчивости, предложенный в 1936 г. А. в. Михайловым. Так же, как и алгебраические критерии, частотные критерии вытекают из непременного условия наличия только левых корней в характеристическом уравнении устойчивой линейной динамической системы. Не останавливаясь Нй доказательстве критерия А. в. Михайлова, рассмотрим его иракское использование для анализа устойчивости. С этой целью характеристическое уравнение запишем в виде

оР + aip -i Н-----Ь ttn-ip + an = F{p). (2.65)

Положив в (2.65) р-](о и отделяя вещественную часть от мнимой, полином F(p) приведем к виду

/=(/0)) = f/(co) +/V(to), (2.66)

где и((о) - вещественная часть - сумма всех членов, содержащих / в четных степенях; V--мнимая часть выражения (2.66). в соответствии с критерием Михайлова условие устойчивости

- Aargf (/ю) = п^, 0<сй<оо. (2.67)

Геометрическое место точек конца вектора Р(](о) при изменении частоты в диапазоне 0<;й<;°° называется годографом вектора, или годографом Михайлова. в соответствии с (2.67) критерий Михайлова формулируется следующим образом: динамическая система, описываемая линейным дифференциальным уравнением п-го порядка, устойчива, если при изменении со от О до оо годограф вектора Р(}(о) последовательно проходит в положительном направлении (против часовой стрелки) п квадрантов комплексной плоскости. На рис. 2.6 приведены примеры годографов устойчивых и неустойчивых систем.

Амплитудно-фазовый критерий устойчивости - критерий Най-квиста. Этот критерий основан на связи свойства устойчивости замкнутой системы с формой АФХ разомкнутой устойчивой системы. Вопрос же об устойчивости разомкнутой системы решается обьино легко. в соответствии с критерием Михайлова разомкнутая устойчивая система с передаточной функцией Wp(p)Kp(p)IHp(p) отвечает условию

Д arg/fp(/cu) = п--, 0<а<оо, (2.68)

где п порядок характеристического полинома Нр(р)-0.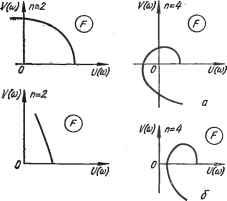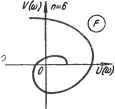

©

Рнс. 2.6. Годографы систем:

а - устойчивых; б - неустойчивых

АФХ замкнутой системы описывается выражением

Ц7з(/со) = lip(/co)/[14- Wp(/co)].

Обозначим знаменатель полученного выражения через WiQai), т. е.

/Ср(/(о) (/ш) 1Г.(/со)==1+1Гр(/со)==1+- = -, (2.69)

где H(j(3i)-K{j(3i)-\-H(j(3i)-характеристический полином замкнутой системы при р=/сй.

В соответствии со свойствами передаточных функций порядок полинома Н(р) не превышает порядка полинома Н^(р), так как Н(р)=Кр(р)-[-Нр(р), а порядок полинома Кт?(р) меньше порядка полинома ЯрСр).

Поэтому критерий Михайлова для замкнутой системы можно записать в виде

А arg Я (/ю) = {п - 2т)~, О < to < оо, (2.70)

где т - число правых корней системы, имеющей в замкнутом состоянии характеристический полином Н(р) - 0.

Коэффициент 2 перед т введен потому, что каждый правый корень не только не обеспечивает положительного поворота вектора, но и создает его отрицательный поворот (по часовой стрелке).

Из (2.69) вытекает, что

А arg Wi (/ю) = А arg Я (/ю) - А arg Яр (/to). Или, учтя (2.68) и (2.70), получаем

А arg Wi (/со) = (м - 2m) 4- - =

2 2

В устойчивой замкнутой системе правых корней в характерис-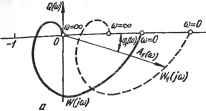

Рис 2.7. Амплитудно-фазовый критерий устойчивости (критерий Найквиста):

а - частный случай; б - общий

тическом уравнении нет, т. е. пг=0, следовательно, условием устойчивости замкнутой системы будет

А arg ITi (/to) = 0. (2.71)

З'словие (2.71) выполняется только тогда, когда кривая lFi(/toj при изменении частоты от О до о° не охватывает начала координат .омплексной плоскости P(to); /Q(to), где P(to) -вещественная часть выражения Wi(/co), Qto) - мнимая часть (рис. 2.7). Действительно, только в этом случае результирующий поворот вектора IFiC/to) при изменении to от О до °о будет равен нулю, так как возрастание угла ф(ш), обусловленное движением вектора IFiC/to) в положительном направлении (против часовой стрелки), будет компенсироваться таким же убыванием ф((й), обусловленным движением вектора WiC/to) в отрицательном направлении (по часовой стрелке).

Как видно из (2.69), переход на комплексной плоскости от годографа вектора WiC/to) к годографу вектора АФХ разомкнутой системы WpC/to) осуществляется сдвигом кривой WiC/to) влево на -1, так как W{\iss) = W,{\ii,) - 1.

Выполнив эту операцию, получаем следующую формулировку амплитудно-фазового критерия устойчивости - критерия Найквиста: линейная динамическая, система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФХ разомкнутой системы при изменении частоты от О до °о не охватывает на комплексной плоскости точку с координатами (-1; /0) (рис. 2.7, а).

Более общая формулировка критерия Найквиста относится к системам, имеющим так называемую АФХ второго рода (рис. 2,7, б), когда WpC/to) несколько раз пересекает вещественную ось левее точки / (©)= -1. В этом случае условимся считать положительным переход годографа через вещественную ось, если он совершается сверху вниз, и отрицательным, если он совершается снизу вверх. Тогда формулировка критерия Найквиста принимает вид: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменений астоты от О до -}-оо разность между числом положительных пере-ходов^годографа АФХ разомкнутой системы через участок вещественной оси (-1, -оо) JJ числом отрицательных переходов равна нулю. Из этого условия видно, что система, устойчивая в разомк-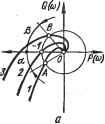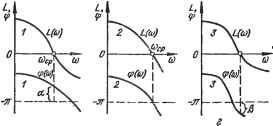

Рис. 2.8. Логарифмический критерий устойчивости

нутом состоянии и имеющая АФХ в форме кривой, показанной на рис. 2.7, б, устойчива и в замкнутом состоянии.

Логарифмический критерий устойчивости. Этот критерий основан на связи свойств устойчивой замкнутой динамической системы с формой ЛАФЧХ разомкнутой системы (рис. 2.8).

В соответствии с критерием Найквиста устойчивая разомкнутая система, имеющая АФХ в форме кривой 1, устойчива с запасом по фазе, равным а. При этом под запасом по фазе понимается угол между отрицательным направлением вещественной оси и прямой, соединяющей начало координат с точкой А - точкой пересечения АФХ разомкнутой системы с окружностью единичного радиуса.

Система, имеющая в разомкнутом состоянии АФХ в форме кривой 2, будучи устойчивой в разомкнутом состоянии, ,в замкнутом состоянии находится на границе устойчивости (запас по фазе равен нулю). Наконец, разомкнутая устойчивая система, имеющая АФХ в форме кривой 5, в замкнутом состоянии будет неустойчивой с недостатком фазы, равном (3. Нетрудно заметить, что этим трем случаям соответствуют логарифмические амплитудно-фазовые частотные характеристики, помеченные теми же индексами, что и АФХ. Анализируя формы ЛАФЧХ для устойчивых и неустойчивых систем, можно сформулировать следующий логарифмический критерий устойчивости: динамическая линейная система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если на всем диапазоне частот, на котором L((b)>0, значение фазы ф(<й)>-180° или (равносильно) на всем диапазоне частот 0< <<а<<аср фазовая характеристика не пересекает линии - я. Под частотой среза Шср понимается частота, при которой L((b) пересекает ось частот.

Для устойчивых разомкнутых линейных систем, имеющих АФХ второго рода (рис. 2.7, б), логарифмический критерий устойчивости может быть сформулирован так: линейная динамическая система, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом, если на всем диапазоне частот, на котором .L (( )>> О, количество положительных переходов фазовой характеристики ф(<а) через линию - я равно количеству отрицательных переходов (рис. 2.9).

Выделение областей устойчивости. Критерий Вышнеградского.