Рис. 2.9. Общий случай логарифмического критерия устойчивости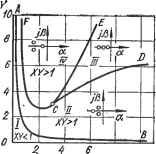

в 10 X

Рис. 2.10. Диаграмма Выш-неградского

наладке и эксплуатации линейных динамических систем возникает необходимость изменять отдельные параметры системы, следовательно, неоднократно проверять систему на устойчивость. Поэтому важное значение имеют методы, позволяющие определить-область изменения тех или иных параметров, допустимую с точка зрения условий устойчивости. Так как коэффициенты характеристического уравнения системы определяются 4ej)e3 ее параметры, то поставленная задача может рассматриваться как задача определения допустимого по условиям устойчивости диапазона изменения коэффициентов характеристического уравнения.

Такая задача для диапазона изменения двух параметров была впервые поставлена и решена русским инженером и ученым И. А. Вышнеградским. Результат решения известен под названием диаграммы Вышнеградского, широко и успешно применяемой в практике анализа и синтеза линейных систем автоматического управления. \

Критерий Вышнеградского обоснован для систем, описываемых линейными уравнениями третьего порядка, но идеи, заложенные в этом критерии, оказали большое влияние на развитие теории устойчивости линейных динамических систем.

Пусть имеется система, характеристическое уравнение которой имеет вид

или

Copf + aip2 4- -f Оз == О

рЗ + cip2 + С2Р + Сз = о,

(2.72) (2.73>

где ci = Ci/co; = azK; Cs = афо-

3 . 3 3

-Делаем подстановки: р = Z-j/cs; ci = X-Cs, = УУс^

или Z = p/y X = У = ЫЩ.

С учетом этих обозначений уравнение (2.73) примет вид Z + XZ-+YZ+l ==0.

Если система находится на границе устойчивости, то уравнение (2.73) будет иметь один действительный отрицательный корень и два мнимых корня:

pi = -а; Р2 = -/Р; рз - - /р.

Левую часть уравнения (2.73) можно разложить на множители:

pS } с,р2 , } + Сз = (р + а) (р - /р) (р + /р) =

= (Р + а) (р2 + Р^) =Р^ + р'а + рр2 + ар2.

Приравнивая в этом уравнении коэффициенты при одинаковых степенях р, находим Cj-сс,С2=р2, Сз=ар2. С учетом этих соотношений справедливо

cicz - сз = 0. (2.74)

Выразив в (2.74) коэффициенты через X nY, получим

XY-l=0,T. е. XY=l. (2.75)

Это уравнение является уравнением гиперболы, коэффициенты которого выражены через коэффициенты характеристического уравнения системы, т. е. через ее параметры. При этом, как следует нз приведенных рассуждений, все точки в плоскости Y, Z, лежащие на гиперболе (2.75), соответствуют таким значениям параметров системы, при которых эта система находится на границе устойчивости. Геометрическое место точек в плоскости параметров линейной динамической системы, описываемой дифференциальным уравнением третьего порядка, соответствующее состоянию системы на границе устойчивости, называется гиперболой Вышнеградского - уравнение (2.75) и рис. 2.10. Гипербола Вышнеградского разбивает плоскость Y, X на две области: XY<1 (область I) и ХУ>>1 (область И). Для выяснения вопроса об устойчивости системы с параметрами, лежащими в областях I и П, примем в уравнении (2.73) Сз=0. Тогда получим: р=0; p+Cip+C2=0. Второе уравнение будет иметь корни с отрицательными вещественными частями при условии Ci>>0; С2>0. Учитывая, что Сз==0, приходим к выводу, что два корня имеют отрицательные вещественные части при условии

cics - Сз > 0. (2.76)

Это условие остается справедливым и в случае, когда сз отличается от нуля, так как при малом изменении Сз корни уравнения (2.73) изменяются мало, согласно теореме о непрерывной зависимости корней характеристического уравнения от его коэффициентов. Следовательно, условие (2.76) является условием устойчивости системы, которое, с учетом значений Ci, с^ и сз, может быть заменено условием

Таким образом, область параметров системы, расположенная выше гиперболы Вышнеградского (рис. 2.10), соответствует области устойчивости, а область, расположенная ниже гиперболы,- неустойчивая область.

На основании сказанного критерий устойчивости Вышнеградского формулируется так: линейная динамическая система, описываемая дифференциальным уравнением третьего порядка, устой-

чива, если при положительных коэффициентах характеристического уравнения выполняется условие XY>1.

Устойчивую область на диаграмме Вышнеградского можно разбить на ряд подобластей с одинаковым характером устойчивого переходного процесса. Например, анализ уравнения (2.73) из условий наличия трех вещественных отрицательных корней позволяет выделить кривую ECD, описываемую уравнением 4(х^+у^) -

- 18хг/-}-27=0, которая на диаграмме выделяет область III.

В пределах этой области параметры системы обеспечивают отрицательные вещественные корни, т. е. обеспечивают апериодический переходный процесс в системе.

Рассуждая аналогично, можно получить уравнение кривой FCE: (2х^ - 9ху -{- 27 = 0), выделяющей в плоскости X, Y область IV с параметрами системы, обеспечивающими один вещественный отрицательный корень и два комплексных корня с отрицательной вещественной частью. При этом вещественные части комплексных, корней по абсолютному значению больше вещественного корня, что-соответствует монотонным переходным процессам. Наконец, в об-jiacTH II имеют место один вещественный отрицательный корень и два комплексных корня с отрицательной вещественной частью. При этом вещественный корень по абсолютному значению больше: вещественной части комплексных корней, что соответствует колебательным переходным процессам.

Таким образом, диаграмма Вышнеградского представляет собой плоскость двух параметров линейной динамической системы третьего порядка с выделенными устойчивыми и неустойчивыми областями параметров системы и областями, соответствующими апериодическим и колебательным переходным процессам. По диаграмме легко определяется диапазон изменения двух параметров линейной динамической системы, обеспечивающий тот или иной переходный процесс в системе.

Выделение областей устойчивости в плоскости параметров линейной динамической системы, описываемой дифференциальным уравнением л-го порядка, осуществляется на базе общего метода -разбиения, рассматриваемого в специальных курсах по теории автоматического управления. Этот метод базируется на анализе характеристического уравнения линейной системы. Он позволяет сравнительно легко определить допустимые с точки зрения устой- чивости диапазоны изменения одного или двух коэффициентов ха- рактеристического уравнения, выражаемых через параметры системы.

2.5. КАЧЕСТВО УПРАВЛЕНИЯ В ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМАХ

Под качеством управления понимается характер переходных процессов в системе, вызванных управляющими и возмущающими воздействиями. Законы изменения величин, характеризующих систему, задаются. Исследование качества процесса управления сводится, таким образом, к определению действительного характера

переходных процессов в системе и сопоставлению его с заданными законами. Если система не удовлетворяет требуемым показателям качества управления, то в нее вводятся дополнительные элементы - корректирующие устройства, которые, не нарущая основного назначения системы, обеспечивают требуемое качество управления.

Для оценки качества управления необходимо располагать количественными или качественными показателями, характеризующими формы переходных процессов в системе.

Оценки качества управления могут быть косвенными или прямыми.

Косвенные оценки получают на основе анализа тех или иных характеристик системы, например частотных. Косвенные методы оценки позволяют получить некоторые параметры переходного процесса, например установить его принципиальный характер - сходящийся он или расходящийся.

Среди косвенных методов оценки качества процесса управления получили распространение корневые, интегральные и частотные методы.

Корневые методы вытекают из наличия связи между формой переходного процесса в системе и характером распределения на комплексной плоскости корней характеристического уравнения. Например, ранее было показано, что если имеется хоть один правый корень, то переходный процесс в системе будет расходящимся. Корневые методы наиболее эффективны, если удается выполнить анализ не только полюсов, но и нулей передаточной функции исследуемой системы. При этом под полюсами понимаются корни знаменателя передаточной функции, т. е. характеристического полинома Н(р)=0, а под нулями - корни числителя передаточной функции, т. е. полинома К(р) =0.

Вместе с тем корневые методы наиболее полно разработаны для систем с передаточными функциями вида W(p)=k/H(p), т. е. с передаточными функциями, не содержащими нулей.

В интегральных методах оценками качества служат определенные интегралы по времени от некоторой функции физических величин, характеризующих системы, вычисляемые без решения дифференциального уравнения системы. Интегральные методы наиболее удобны для сравнительной оценки обобщенных показателей качества в системах управления, близких по некоторым свойствам.

Частотные методы базируются на связи между формой переходного процесса в системе и вещественной частью частотной характеристики. Эти методы позволяют приближенно построить всю кривую переходного процесса, не прибегая к решению дифференциальных уравнений, описывающих исследуемую систему.

К прямым оценкам относятся количественные показатели формы переходного процесса физических переменных в системе при заданных воздействиях на нее. Прямая оценка качества может быть получена лишь после того, как построена интересующая нас зависимость x(t).

Построение переходных процессов операторным методом. Операторный метод анализа качества управления базируется на ис-

пользовании передаточной функции системы, из которой можно получить изображение искомой величины

х(р) =K(p)/Hip)F{p), (2.77)

где F(p)-преобразованная по Лапласу функция воздействия на систему (возмущающего или управляющего).

Располагая изображением искомой переменной х(р) и применяя обратное преобразование Лапласа, можно определить переходный процесс в системе, т. е функцию x(t).

Вь1ражение (2.77) позволяет найти изображение функции переходного процесса лишь при нулевых начальных условиях, что вытекает из определения передаточной функции системы. Как известно, начальные условия будут нулевыми тогда, когда в начальный момент воздействия на систему сама функция x(t) и все ее производные до (л-1)-й включительно равны нулю. Начальные условия зависят от состояния системы в момент приложения возмущающего воздействия и от его формы, которая определяется видом полипома К(р) - полинома числителя передаточной функции сис-те1ы. Можно выделить следующие обстоятельства, обеспечивающие нулевые начальные условия: 1) начальные условия будут нулевыми при любом воздействии на систему, если в момент его приложения система находилась в равновесном состоянии, а полином K(p)-k, т. е. не содержит р; 2) система в момент приложения воздействия находилась в равновесном состоянии, в числе членов полинома К{р) имеются такие, которые содержат р, но все производные функции воздействия на систему, вплоть до т-й включительно, при =0 равны нулю (здесь т - порядок полинома К(р)); 3) система находилась в неравновесном состоянии, полином К(р) содержит члены, содержащие р, но форма возмущающего воздействия такова, что при /=0 каждый член правой части дифференциального уравнения движения системы, содержащий производную воздействия на систему до т-й включительно, уравновешивается соответствующим членом левой части уравнения, содержащим про-. изводную возмущения того же порядка. При ненулевых начальных условиях изображение выходной величины системы имеет вид

К(р) М(р)

где М(р) - полином, учитывающий влияние ненулевых начальных условий.

Для множества случаев изображение функции воздействия на систему имеет вид дробно-рационального выражения F(p) = =-1 (р)/2(р). Тогда (2.78) принимает вид

К(р)Рг(р)+Р2{р)М{р) Р' - H(p)F,(p)

Линейные динамические системы часто исследуются в режиме воздействия в форме единичного скачка /:

О при < О F при f > О

t=f{t)

в этом случае

F(p)=f/p; рЛр)=Г, Ыр)=р-

Тогда (2.78) примет вид

. . K(p)J+pM(p)

-WW)-

Если в (2.79) корни полинома Н(р) = 0 будут простыми (не кратными) и при =0 система находится в равновесном состоянии, то, используя формулу разложения Хэвисайда, получим

где

k=i

Hip) =

ePht, (2.80)

n - порядок полинома Н(р) =0; pi, рг.....Рп - корни полинома

Я(р) = 0; К{0) = К{р) и Я(0) = Я(р) при р = 0.

На основании свойств полинома Я(р) = О, его можно представить в виде Я(р) = ао{р -pi) ... (р -pk) .-Ар -Рп) =

= ОоП (Р -Рь); Н'(р) = (Pft -Pi) ... (Pft -р ) = П iPh - Pq).

Тогда (2.80) можно переписать так:

К(0) ri Kip)

=1 Ph л (Ph - Ря) 3=1, дфк

Выражение (2.81) позволяет построить переходный процесс x(t) в линейной динамической системе при единичном воздействии.

Операторный метод построения переходных процессов становится неудобным для систем высокого порядка, так как требуется большой объем вычислений.

Построение переходных процессов частотным методом. Метод базируется на использовании частотной характеристики Р(<а) - вещественной части выражения передаточной функции W(p) системы при p-ja:

1Г(/ш) =Р(ш)+/Q(£d).

Не останавливаясь на доказательстве, укажем, что между функциями x(t) и Р(а>) имеют место следующие зависимости:

2 г Р(а>)

x(t) = - J --sin Ша (2.82)

о

или

2 f о (о)

x{t) = Р (0) Ч- - J -- COS Ша. (2.83) о

Функции Р(а) и 0((а) имеют сложный характер, вследствие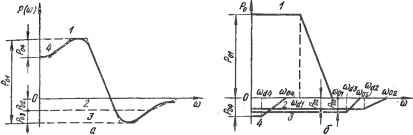

Рис. 2.11. Вещественная частотная характеристика и ее составляющие

чего их трудно описать аналитически. Поэтому переходные процессы непосредственно по выражениям (2.82) и (2.83) на практике не рчссчитываются. Однако расчет существенно упрощается, если -Кривую Р(а) (рис. 2.11) заместить совокупностью трапеций:

Р(С0) =I]Pi(£0), г=1

где i - номер трапеции.

Каждой составляющей Рг(а>) соответствует переходный процесс вида

Xi{t)

sin atda.

Таким образом.

(2.84)

Выражение (2.84) лежит в основе метода расчета переходных процессов в линейных динамических системах с использованием вещественной частотной характеристики Р((а). Для практической реализации метода каждую t-ю трапецию (рис. 2.11) определим следующими параметрами: Рог - высота; cooi - интервал пропускания частот; - интервал равномерного пропускания частот; v=(Bdi/cuoi - коэффициент наклона. Кроме того, вводится понятие типовой единичной трапеции, для которой принято Ро=1, <ао=1 при любом значении v.

Зависимость (2.82) для случая, когда Р((а) замещается типовой единичной трапецией, дает следующее выражение переходного процесса:

hir) =

Jl(l-V)

Si(T) - vSi(vT) -f

COS T-COS VT

(2.85)

где Si(T) - интегральной синус выражения J dr.

Функция /г,-(т) легко преобразуется в соответствующую функцию Xi(t) путем пересчета масштабов по осям. На основании связи

характера функции Р((а) и формы переходного процесса этот пересчет осуществляется так:

Хг (t) = hi (Т) Рог; t = Т/Шог- (2.86)

Значения функции h(x) для различных значений v и т рассчитаны и сведены в таблицы, которые позволяют легко получить точки кривой Xi(t).

На основании изложенного порядок построения графика переходного процесса в линейной динамической системе при единичном воздействии на входе с использованием вещественной частотной характеристики сводится к такой последовательности операций:

1) на основе передаточной функции системы W(p) путем замены р=/<а и отделения вещественной части от мнимой находится характеристика РС<а);

2) функция Р((а) разбивается на трапециевидные составляющие, для каждой из которых определяются параметры Рог, (Иоь Шг и v;

3) с помощью таблиц находятся /i-функции. для относительного времени т;

4) используя соотнощения масштабов, определенные выражениями (2.86), осуществляется переход от функции Ы(г) к функции Xi(t);

5) определяется кривая переходного процесса в системе как алгебраическая сумма кривых Xi(t):

x(t) =txi{t),

где n - число трапеций, которыми замещена характеристика Р(а).

Рассмотренный метод можно распространить на построение переходных процессов при воздействии, отличающемся от единичного, о чем пойдет речь ниже.

Как, отмечалось, переходные процессы в линейных динамических системах строятся обычно для замкнутых систем. Поэтому наиболее трудоемкой частью расчета является определение характеристики Р(а) замкнутой системы. Эта часть расчета существенно упрощается при использовании для определения вещественной частотной характеристики РС<а) замкнутой системы характеристик L((b) и v(tu) разомкнутой системы. В теории автоматического управления широко используются номограммы для определения функции Р((в) замкнутой системы по логарифмическим амплитудно-фазовым частотным характеристикам разомкнутой системы.

От переходного процесса, вызванного единичным входным воздействием, можно перейти к переходному процессу от произвольного воздействия u(t), используя интеграл Дюамеля, или свертки:

x{t) = f u{t-~r)(i> (т)dr (2.87)

о

или

x{t) = f(i>(t-t)u{r)dr, о

,дц момент приложения воздействия u(t); - импульсная

переходная функция.

Импульсная переходная функция ш(и представляет собой переходный процесс в системе, к которой приложено импульсное воздействие в виде б-функции, отвечающей условию

]b{t)dt=\; б(р)=1, (2.88)

о

при этом 6(0 существует только при =0.

Нетрудно убедиться, что между импульсной переходной функцией со ( О и функцией h(t) существует зависимость

со()=Й(0, (2.89)

т. е. ©СО представляет собой первую производную по времени /i-функции - функции переходного процесса при единичном возмущении.

2.6. КОРРЕКЦИЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

Линейную динамическую систему, элементы которой рассчитаны из условий обеспечения статических режимов работы, назовем исходной системой. Исходная система может оказаться неудовлетворительной с точки зрения требований динамики, т. е. неустойчи- вой или устойчивой, но не обеспечивающей требуемых форм переходных процессов. В таких случаях исходная система дополняется специальными элементами - корректирующими устройствами (КУ), которые вводятся в систему с целью придания ей необходимых динамических свойств, не изменяя основного назначения системы, определяемого условиями работы объекта управления.

По характеру включения корректирующих устройств в исходную систему их можно разделить на две группы - последовательные корректирующие устройства (КУ) и параллельные. Первые включаются последовательно с элементами исходной системы, вторые- параллельно каким-либо элементам. Параллельные КУ являются местными обратными связями, которые могут быть как отрицательными, так и положительными.

Остановимся на одном, простом и эффективном способе определения математических моделей КУ и соответствующих этим моделям физических элементов, образующих корректирующие устройства. Способ базируется на использовании так называемых желаемых логарифмических амплитудно-частотных характеристик {Ьш). Желаемой ЛАЧХ называется такая характеристика LCco), которая соответствует линейной динамической системе, полностью отвечающей требованиям, предъявляемым в динамических режимах. Можно сформулировать требования к форме i-m для широкого Круга статических и астатических систем.

Наибольшее влияние на динамику оказывает форма Lh<C<o} в районе частоты среза соср- В связи с этим весь диапазон частот характеристики Ьш(со) (рис. 2.12) разобьем на три части: участок низких частот (0<co<coi); участок средних частот (со2<м<соз); высокочастотный участок (со>из).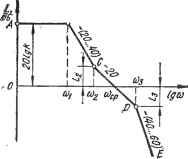

Рис. 2.12. Характеристика Lh<(w)

Построение характеристики -ш(со) начинается с выбора значения частоты соср, которая прямо связана с быстродействием системы. Меньшие значения соср соответствуют меньшему быстродействию системы, т. е. отражают большую длительность переходных процессов. При выборе значительных частот Шср для характеристики Ьш(со) могут возникнуть непреодолимые трудности в практической реализации этой характеристики, так как потребуются очень сложные, вплоть до нереализуемых физическими элементами, корректирующие устройства.

В практике проектирования линейных динамических систем широко используются зависимости, связывающие значения соср с величинами /max и бтах, где /max - максимальное время переходного процесса; бтах - максимальное перерегулирование. Используя эти зависимости, можно выбрать значение соср, обеспечивающее требуемые показатели качества управления в проектируемой системе.

Анализ систем, имеющих высокие динамические качества, показывает, что ЛАЧХ таких систем должна иметь в районе частоты среза наклон -20 дБ/дек. Следовательно, среднечастотный участок характеристики ЬшСсо) представляет собой линию CD (рис. 2.12), проходящую через точку <оср с наклоном - 20 дБ/дек. Границы участка CD определяются ординатами и Lz, соответствующими частотам сог и соз, которые также могут быть определены по заданным значениям бтах.

Участок характеристики L,kCco) правее точки D проводится с таким наклоном, который имеет ЛАЧХ исходной системы в этом диапазоне частот, так как высокочастотный участок характеристики LffiCco) практически не влияет на показатели качества управления.

Низкочастотный участок Ьж(со) для статических систем представляет собой прямую АВ, параллельную оси частот и проходящую на высоте 20 IgA, где k - коэффициент усиления исходной разомкнутой системы. Для астатических систем этот участок характеристики представляет собой прямую линию с наклоном -20 V дБ/дек., где v - порядок астатизма, проходящую через точку с координатами [со -1; /.(со) =20 Igfe]. Наконец, низкочастотный и среднечастотный участки ЛАЧХ сопрягаются отрезком ВС (или более чем одним отрезком). Наклон отрезка ВС выбирается из условия, чтобы перепад наклонов двух соседних отрезков характеристики LhiCco) не превышал 40 дБ/дек. Это требование вытекает из возможностей реальных физических элементов, с помощью которых реализуется характеристика 1жГсо).

Для определения типа и параметров КУ на базе использования характеристики Lm(co) необходимо сравнить эту характеристику с ЛАЧХ Lncxfco) исходной системы и установить вид ЛАЧХ требу-