емого корректирующего устройства, т. е. форму характеристики

Если синтезируется последовательное КУ, то WcAp) Wcx{p)W.y{p),

где Wck(p), Wscx(p) - передаточные функции соответственно скорректированной и исходной систем; К^к.у(р)-передаточная функция последовательного корректирующего устройства.

Переходя от передаточных функций к АФХ, а затем к ЛАЧХ,

получим Z-ck(co) = Lhcx(cu) -f- Ьк.у(со).

Так как цель коррекции сводится к тому, чтобы преобразовать исходную систему в желаемую с точки зрения динамических свойств, то очевидно, что La, (со) =Ьш(со), следовательно, L .y(co) = =:Lffi(co)-Lhcx(co). Таким образом, если из ординат характеристики вычесть ординаты характеристики Lhcx(co), то получим ординаты ЛАЧХ последовательного КУ. Далее по виду Ьк.у(со) можно выбрать физические элементы, реализующие эту ЛАЧХ, т. е. выбрать физическую схему и параметры КУ-

х1ри выборе параллельного КУ

WoMp)W.o(p)

vmp) - 1 + Wo.b(p)W .y(p)

где Woxe(p), Ws.o(p) - передаточные функции части исходной системы соответственно охваченной местной обратной связью (параллельным КУ) и не охваченной ею. Переходя к АФХ, получим

Гожь(/СО)Гн.о(/СО)

Для диапазона частот, в котором ] 11охв(/со) к.у(/со) I 1, имеем WcK(h) та 11н.о(/со)/к-у(/м). Переходя к ЛАЧХ, получим

jfk.y(co) = Lh.o(co) - Lck(co),

Т. е. ЛАЧХ параллельного корректирующего устройства имеет вид

Ьк.у (со) = Lh. о (со) - 1исх (со) .

На основе последнего выражения можно определить логарифмическую частотную характеристику параллельного КУ, выбрать физические элементы и их параметры, реализующие Ьк.у(со). В практике проектирования линейных динамических систем широко используются таблицы, содержащие физические схемы КУ, их передаточные функции и характеристики Ьк.у(со). В таких случаях задача выбора КУ сводится к определению вышеуказанным способом формы Ьк.у(со) и выбору в таблицах необходимого типа корректирующего устройства.

Целесообразно подчеркнуть, что решение задачи выбора КУ неоднозначно, так как одни и те же динамические характеристики можно обеспечить различными физическими элементами, образующими корректирующие устройства. Например, в практике автоматического управления широко используются параллельные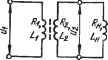

-о^о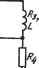

Off в

Рис. 2.13. Корректирующие устройства, реализующие местную гибкую обратную

связь:

а -. стабилизирующий трансформатор: б - динамический мост; е - ЛАХ

КУ, реализующие гибкую обратную связь по различным физическим переменным, подаваемым на вход КУ, с выхода охваченной части линейной системы. Такие КУ имеют передаточную функцию вида

=r2(p)/(r,p-f 1).

Эту передаточную функцию и соответствующую ей Ьк.у(со) можно реализовать с помощью нескольких устройств, часть из которых приведена на рис. 2.13. Постоянные времени и коэффициенты усиления их определяются так:

для стабилизирующего трансформатора

R2-\-Rm

для динамического моста

= Tikyi;

R*

R1 + R2 ~ Ri + R4

Глава 3

НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ

3.1. ОПРЕДЕЛЕНИЕ И ОСОБЕННОСТИ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ

Нелинейными называются системы, содержащие нелинейные элементы (НЭ), т. е. такие элементы, у которых соотнощения между выходными и входными величинами описываются нелинейными уравнениями. Строго говоря, все динамические системы являются нелинейными. В этом смысле линейные методы анализа и синтеза динамических систем управления неприемлемы. Однако линейные модели реальных нелинейных систем во многих случаях могут с достаточным приближением отражать свойства реальных систем. Кроме того, методы исследования нелинейных систем часто базируются наметодах линейной теории с добавлением тех или иных особенностей, учитывающ,их существование нелинейностей. В целом же тео-

я нелинейных систем является более сложной, менее разработан.-Это в частности, объясняется большим разнообразием типов нелинейных систем, что затрудняет разработку универсальных методов для их исследования. Тем не менее, применение существующих методов исследования нелинейных систем во многих случаях дает достаточно эффективный результат.

Широкий круг нелинейных динамических систем содержит нелинейные элементы с типовыми нелинейностями, под которыми понимаются определегшые статические зависимости лгвых =!{хех). Некоторые из этих зависимостей приведены в табл. 3.1. Нелинейные элементы, у которых зависимость л:бых=/(->вх) одинакова как при возрастании величины лгвх, так и при ее убывании, называются не-линейными элементами с однозначными статическими характеристиками. Нелинейные элементы, у которых при возрастании Хвх имеет место одна зависимость л;вых=/(л:вх), а при уменьшении Хвх - другая, называются нелинейными элементами с неоднозначными статическими характеристиками.

Неоднозначные статические характеристики отражают наличие гкс ерезисных явлений в соответствующих устройствах автоматики.

Нелинейные элементы обусловливают существенные отличия свойств нелинейных систем от линейных, что требует разработки иных методов исследования. Характер возможных движений в нелинейных системах более широк, чем в линейных. Действительно, в линейной системе движение может быть либо сходящимся, если система устойчива, либо расходящимся, если система неустойчива. Существование устойчивых колебательных движений в линейных системах недопустимо, так как означает нахождение системы на границе устойчивости. Такой режим работы линейной системы практически невозможен, поскольку при любом незначительном изменении ее параметров движения координат системы станут либо сходящимися либо расходящимися. В нелинейной же системе возможны устойчивые колебательные движения тех или иных переменных при отсутствии внешних периодических возмущений. Такие движения называются автоколебаниями, а системы - автоколебательными. Амплитуда и частота автоколебаний определяются параметрами системы. Следовательно, в одной и той же нелинейной системе могут быть несколько режимов автоколебаний.

Автоколебания могут быть нежелательными или недопустимыми. В таком случае параметры системы выбираются из условий невозможности автоколебательных режимов. Однако автоколебания могут быть необходимыми, обеспечивая принцип работы конкретной динамической системы, например вибратора-уплотнителя какой-либо массы. В этом случае параметры системы выбираются из условий обеспечения требуемых устойчивых автоколебательных режи-

Природа возникновения автоколебаний связана с тем, что коэффициент усиления нелинейной системы на разных участках статической характеристики различен, что вызывает автоматический переход от расходящихся движений к сходящимся и наоборот.

Таблица 3.1

Графическая зависимость

Тип нелинейности

Анэлитическан зависимость

arc tg к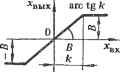

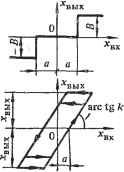
~а2 -в1

п

+ 1 +Д2 вх

Нечувствительность

Ограничение (насыщение)

Релейная

Релейная с зоной нечувствительности

Зазор (гистерезис)

Релейная с гистерезисом

Релейная с нечувствительностью и гистерезисом

Хъык= при лгвых' <а

Хвь,к = ~ + 1<к при ЛГвых^

ьык = -Хвк при х^<-а

,=to при \х^\ < f

вых= при bgl > -вых = --В при < - f-

вых=- при Хз>0

*вых

= -В при лг..<0

bbrx=-S при :<з^>д вых=0 при -fl<Xg<-fl вых = - при х^.<-а

вык = -<вx при лг>д

*bbix = f -<*bx при х'<-а

=0 при <д

л;вых=5 при х^>а Хъых = -В при лгвх<а.

вых= при Хвх>-а %ых = - -В при < - д

л;вых= при Х^>а2 вых = 0 при -с, <Хзх<йг л:вых=-й при лгвх<-а1

л:вых= при x>ai лгвых=0 при -а2<лгз^<а,

bb.x = --g при Ха<-Д2

вх>0

*вх>0

вх<0

в нелинейных системах существенно изменяется постановка и оешение задачи анализа устойчивости. Как было показано в предыдущей главе, устойчивость линейной системы зависит только от свойств системы и не зависит от отклонения переменных в начальный момент. В нелинейной же системе, устойчивой при малых отклонениях, могут возникать неустойчивые режимы при больших начальных отклонениях. В связи с этим для нелинейной системы вводятся понятия устойчивость в малом и устойчивость в большом .

Широкий класс нелинейных динамических систем может быть описан уравнением вида

-=fi{Xi,X2,...,Xn), (3.1)

где Xi - координаты системы; ft, i= I, п - непрерывные или кусочно-непрерывные функции.

Г бенность уравнений типа (3.1) состоит в том, что под знаком нелинейной функции стоят только сами переменные, без производных, а исходная система уравнений, описывающих нелинейную систему, решена относительно первых производных всех координат по времени. К числу систем, описываемых уравнением вида (3.1), откосятся системы с выделенным нелинейным элементом, например элементом с типовой нелинейной статической характеристикой. Такая система может быть представлена как последовательное соединение линейной части (ЛЧ) и нелинейного элемента (НЭ), что в значительной степени упрощает исследование системы.

Точные методы анализа нелинейных динамических систем применимы лишь для ограниченного круга систем, описываемых уравнениями не выше второго-третьего порядка. Поэтому в теории нелинейных систем широко используются различные приближенные методы: численные, графические, графоаналитические. Использование численных методов связано с необходимостью выполнения громоздких вычислений, а графические методы затрудняют анализ влияния отдельных параметров на динамические свойства нелинейных систем.

3.2. ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ МЕТОДОМ ФАЗОВЫХ ТРАЕКТОРИЙ

Метод фазовых траекторий основан на том, что состояние динамической системы характеризуется положением некоторой точки в плоскости (или пространстве) координат, характеризующей систему. Точка в пространстве координат системы, характеризующая со-состояние системы в любой момент времени, называется изображающей точкой. Ее проекция на оси координат в каждый момент времени дает значение той или иной переменной, характеризующей систему. Переменные оси координат выбираются так, чтобы изображающая точка давала наиболее полную информацию о состоянии системы. Например, если процесс рассматривается на плоскости,

т. е. в системе двух осей, координатными осями могут быть величины

л^вых и Хвх или лгвх и лГвх и т. д. Из сказанного ясно, что метод фазовых траекторий дает наиболее простые и наглядные результаты при исследовании систем не выше втор ого-третьего порядка.

Основные идеи метода фазовых траекторий удобно рассмотреть применительно к линейным системам второго порядка, распространив потом результаты на нелинейные системы. Исходя из этого, обратимся к динамической системе, описываемой линейным дифференциальным уравнением второго порядка или двумя линейными дифференциальными уравнениями первого порядка:

dxi dx2

= axi + Ьхг; = cxi -f ех2, (3.2)

где а, b, с,е - постоянные коэффициенты.

Решить систему уравнений (3.2) -это значит определить переменные Xi и Х2 как функции времени и начальных условий Хю, Хго, т. е. определить Xi=fi(t; Хю; Х20); X2=f2{t; х^; Х20) Удобнее, однако, решение системы уравнений (3.2) представить в плоскости л: Х2, называемой фазовой плоскостью, рассматривая время t как параметр. При таком подходе состояние системы в каждый момент времени характеризуется положением изображающей точки Cf на плоскости переменных Xi, Х2 (рис. 3.1). Начальное положение точки Ci определяется значением начальных условий Хю, Х20. Далее, с течением времени изображающая точка движется по некоторой траектории, определяемой свойствами динамической системы. Геометрическое место изображающих точек на фазовой плоскости (или в фазовом пространстве, если координат более двух) называется фазовой траекторией. Каждому значению начальных условий соответ-

Рис. 3.1. Фазовые траектории и особые точки линейных систем: а - траекторий; б -особая точка типа устойчивый узел ; в - устойчивый фокус ; г- неустойчивый узел ; д - неустойчивый фокус ; е - седло

ствует своя фазовая траектория. Вся совокупность фазовых траекторий на фазовой плоскости (или в фазовом пространстве) называется фазовым портретом системы управления.

Уравнение фазовых траекторий получим, поделив второе уравнение (3.2) на первое и исключив таким образом время:

(3.3)

dxi axi + bxz

Очевидно, что в каждой точке фазовой плоскости выражение (3.3) определяет положение касательной к фазовой траектории, соответствующей заданным начальным условиям. Из (3.3) видно, что любой паре значений Xi и xz соответствует одно единственное dx2

значение -, т. е. в каждой точке фазовой траектории можно

провести лишь одну касательную, а это означает, что фазовые тра-ектории линейной системы на фазовой плоскости не пересекаются. Исключение составляет случай, когда Xi=X2==0 - точка начала кооп; /.jiaT фазовой плоскости. В этом случае, как следует из (3.3), dX2=dxi-0 и положение касательной становится неопределенным: в точке можно провести более одной касательной, а следовательно, фазовые траектории в такой точке пересекаются. Точка на фазовой плоскости, в которой фазовые траектории пересекаются, называется особой точкой. Таким образом, на фазовой плоскости линейной динамической системы имеется лишь одна особая точка, которая находится в начале координат.

В зависимости от характера движения изображающей точки к особой точке особые точки получают то или иное название (рис. 3.1). Очевидно, представленные на рис. 3.1, а, б, в формы фазовых характеристик соответствуют устойчивым системам, а на рис. 3.1, г, д,е - неустойчивым.

Таким образом, фазовые портреты линейных динамических систем полностью отражают характер возможных движений переменных, описывающих эти системы.

Распространим категории и понятия аппарата фазовых траекторий на нелинейные динамические системы, ограничившись системами второго порядка. С этой целью обратимся к нелинейной системе, описываемой двумя нелинейными уравнениями первого порядка: dXi dxz

- = fi{xi,X2); - = F2{xi,X2), (3.4)

где Fy (xi, X2) и F2{xu X2) - нелинейные функции.

JTaK же, как и в линейных системах, уравнение фазовых траекторий получим, поделив второе уравнение (3.4) на первое, исключив тем самым время:

dX2 .2(:1,:2)

dxy ~ F,(xuX2) (-

нейнпй* точки в фазовом пространстве рассматриваемой нелинейной системы определяются как общие корни двух уравнений: Pi {Хи Хг) = 0; Fz {xi, xz) = 0. (3.6)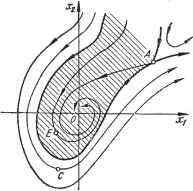

Рис. 3.2. Фазоные траектории нелинейной динамической системы

При этом одна особая точка находится в начале координат, где

Xi = Х2= о и -г- = 0. В линейных dxi

системах функции (3.6) представляют собой прямые линии, которые, пересекаясь в начале координат, естественно, больше в фазовой плоскости нигде не пересекаются. В нелинейных же системах, пересекаясь в начале координат, функции (3.6) в силу нелинейности могут пересекаться также в других точках -фазовой плоскости. Следовательно, на фазовой плоскости нелинейной динамической системы может быть несколько особых точек, а значит, несколько равновесных состояний системы. Особые точки имеют те же названия, что и на фазовых плоскостях линейных систем: узлы, фокусы, седла. На рис. 3.2 в качестве примера приведен фазовый портрет нелинейной системы с двумя особыми точками, одна из которых - устойчивый фокус - находится в начале координат (точка 0), другая - седло (точка А). Как видно из рисунка, характер движения в рассматриваемой системе зависит от начального отклонения ее координат: если начальные отклонения находятся в пределах заштрихованной зоны, движение в системе носит сходящийся характер, а если за ее пределами - движения расходящиеся.

Как отмечалось выше, в нелинейных динамических системах возможны устойчивые автоколебания, т. е. значение переменных, характеризующих систему, может периодически повторяться. Это свойство приводит к возможности появления замкнутых траекторий на фазовых портретах нелинейных систем, которые называются предельными циклами (рис. 3.3). Предельные циклы могут быть устойчивыми и неустойчивыми. В первом случае изображающая точка из любой точки фазовой плоскости стремится попасть на замкнутую траекторию, во втором - уйти от замкнутой траектории либо к началу координат, либо в бесконечность.

Для выяснения устойчивости или неустойчивости предельного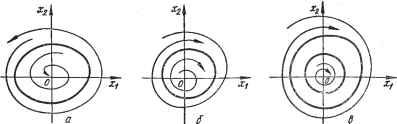

Рис. 3.3. Предельные циклы фазовых траекторий нелинейных систем

цикла необходимо построить две фазовые траектории: одну - внутри предельного цикла, другую - за его пределами и проследить движение изображающей точки по этим траекториям. Предельный цикл, показанный на рис. 3.3, а, является неустойчивым, а сама нелинейная система, имеющая такой фазовый портрет, устойчива в малом и неустойчива в большом. Действительно, если переходный процесс начинается при начальных отклонениях координат xi и Хг, лежащих внутри предельного цикла, то он будет сходящимся. Если начальные отклонения координат находятся за пределами замкнутой траектории, то переходный процесс будет расходящимся.

Рассуждая аналогично, можно убедиться в том, что предельный цикл, представленный на рис. 3.3, б, является устойчивым. Фазовый портрет (рис 3.3, в) содержит два предельных цикла, из которых внешний является устойчивым, а внутренний - неустойчивым. Таким образом, предельные циклы на фазовых портретах нелинейных систем могут играть роль границы устойчивости. При наличии не-ско.: .ix особых точек области устойчивости выделяют незамкнутые кривые, которые называются сепаратрисами. Предельные циклы, особые точки, сепаратрисы определяют топологию фазового портрета конкретной нелинейной системы. При изменениях параметров нелинейной динамической системы в определенных пределах структура фазового портрета может оставаться неизменной. Однако существуют некоторые дискретные значения параметров системы, при которых топологическая структура фазового портрета претерпевает изменения. Эти дискретные значения параметров системы называются бифуркационными.

Полный анализ нелинейной динамической системы включает определение возможных в системе фазовых портретов, бифуркационных границ в пространстве параметров, формы и расположения предельных циклов и сепаратрис по отношению к каждой точке пространства параметров. Однако такой полный анализ нелинейной системы, как правило, выполнить не удается из-за чрезвычайной сложности задачи.

Наиболее часто в инженерной практике встречается задача построения фазовых портретов нелинейных систем, в которых можно выделить нелинейную часть и типовую нелинейность. В этом случае поведение нелинейной системы удается описать совокупностью линейных дифференциальных уравнений, каждое из которых справедливо в пределах соответствующих линейных отрезков типовой нелинейной статической характеристики. После того как определены фазовые траектории, соответствующие линейным дифференциальным уравнениям, на фазовую плоскость наносятся линии переключения , которые представляют собой геометрические места точек фазовой плоскости, где осуществляется переход от фазовых траекторий, соответствующих одному линейному уравнению, к фазовой траектории, обусловленной другим линейным уравнением.

DaTvnuR примера рассмотрим нелинейную систему регулирования темпе-камеры управления ОУ (рис. 3 4), например температуры пропарочной

Температура 6 объекта (рис. 3.4, я) контролируется с помощью электриче-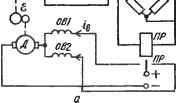

Рис. 3.4. Нелинейная система автоматического регулирования температуры: . а - функциональная схема: б, е - структурные схемы

ской мостовой схемы М, в одно плечо которой включен датчик температуры. При заданном значении G мост уравновешен и напряжение, подводимое к обмотке поляризованного реле ПР, равно нулю. При этих условиях контакт реле ПР занимает среднее положение. При отклонении температуры G от задан-ногб значения контакт ПР замкнет цепь электродвигателя Д на то или иное направление вращения. Двигатель Д через зубчатую передачу воздействует на регулирующий орган РО путем изменения координаты .е, что вызовет изменение подачи теплоносителя х к объекту управления. Направление вращения двигателя определяется тем какая из его обмоток возбуждения - OBi или ОВг - включена, что зависит от положения контакта ПР, а следовательно, от знака отклонения G.

Уравнение объекта управления рассматриваемой системы d%

Т---fG = feoAe или @(р){Тр + \) = kae(p), at

где Т - постоянная времени; ko - коэффициент усиления объекта. Уравнение электродвигателя

e{p)lun(p) =kjp.

Структурная схема, соответствующая написанным уравнениям динамики о учетом характера нелинейности, приведена на рис. 3.4, б.

Объединяя линейные звенья в одну линейную часть (ЛЧ), получим схему, представленную на рис. 3.4, е, откуда видно, что уравнение линейной части системы

р(Тр+1)е(р) =ku(p), (3.7)

где k = о^л - коэффициент усиления линейной части.

Для общности обозначим В == х, а напряжение Мд после включения ПР обозначим Мд = ±В. Тогда, в зависимости от значения Мд, состояние рассматриваемой системы регулирования описывается одним из следующих трех уравнений:

dt dt

= -kB при Мд = -В;

dx dx

dt d4

dt dx

- 0 при Мд = 0;

= kB при Мд = В.

(3.8)

(3.9)

(3.10)

dt dt

Для построения фазового портрета выберем координаты фазовой плоскости