ном временном интервале. Кроме того, хорошее совпадение произ- водных гарантирует и хорошее совпадение самих функций.

В качестве критерия наилучшего совпадения h{t) и f(t) удобно использовать условие минимума среднеквадратичного отклонения сравниваемых величин

min IJl/i {t)-f{t)fdt

(3.2)

Хотя при этом условии несовпадение в отдельных точках может быть значительным, в среднем совмещение должно быть достаточно хорошим.

Для определения условия (3.2) в общем случае можно. юспользо-ваться теоремой Релея, записав

во то-

min { j I /юЯ (/со) - F (/со) \ dco} = min { j \к (/и) - F (/со) Р dco} , (3.3)

t-XX) -СХ)

где Я (/и) и F - спектральные плотности функций h{f)vi f{t) соответственно; К (/оз) - коэффициент передачи (частотная характеристика), представленный в комплексном виде.

Однако вычисление интеграла (3.3) в большинстве случаев сопряжено со значительными трудностями. Поэтому вместо условия (3.2) можно воспользоваться эквивалентным ему соотношением

max/? = max

h(,t)f{t-to)dt

]/]lh(f,]dtju{t-to)]dt

(3.4)

JOTopoe no форме записи аналогично выражению функции взаимной . {орреляции.

Тождественность оценок вида (3.2) и (3.4) можно показать следующим образом. Умножив известную, произвольно смещаемую во времени, функцию / (t- - о) на некоторый лостоянный коэффициент а, запишем новую функцию в виде .

af{t-to)=h(t)+t,(t-to) (3.5)

и подберем величину коэффициента а так, чтобы обеспечивалась ортогональность функций ft (t) и i(t--to) на временном интервале О < то:

то то . то

- ( h{f)Ht-to)dt = ajh (t) f (t -1,) dt - J [ft (/) r dt = 0. (3.6)

Тогда, определив из выражения (3.6) значение h (i) f(t - tg) dt и найдя, что

еж оо оо

f V if - tow *=J i (oi dt+ II (t-t,)r dt, . .:

0 0 0 .

9 R-1id9

после подстановки их в соотнош-ение (3.4) и несложных преобразований получим новое эквивалентное условие

max {R) = max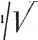

1+ II (t-to)]dt\ lh(t)]dt

(3.7)

Так как в процессе исследования импульсная характеристика остается неизменной, то условие (3.7) сводится к определению

][l(.t-to)Vdt]. (3.8)

Но ? - /о) есть не что иное, как отклонение нормированной определенным образом функции f (t - to) от исследуемой импульсной характеристики:

l(i-to) = af(t-to)-h it).

Следовательно, выражение (3.8) позволяет определить минимум среднеквадратичного отклонения сравниваемых функций. Но зависимости (3.8) и (3.4) тождественны, а значит интегральная оценка (3.4) соответствует условию минимума среднеквадратичного отклонения h(() к af {t - t. При этом произвольный выбор постоянного нормирующего множителя а никак не влияет на условие (3.4).

Соотношение (3.4) по форме записи совпадает с вьфажением функции взаимной корреляции двух случайных зависимостей и, хотя h(,t) Kf{t - to) не являются случайными функциями, отмеченная аналогия дает основания называть метод, базирующийся на оценке (3.4), корреляционным. Однако такое название является чисто условным.

Простая подстановка выражения ft(О и вычисление интегралов в выражении (3.4) не могут являться приемлемыми, так как это не вносит каких-либо упрощений в оценку параметров переходных процессов. Существенных преимуществ можно добиться в том случае, если обойтись без вычисления интегралов и представить их какими-нибудь известными соотношениями, вытекающими из теории линейных цепей. Однако в общем виде при произвольном задании / (t - to) это невозможно. Простота определения выражения (3.4) в значительной степени зависит от удачного выбора аппроксимирующей функции f (t - о)- В представляющих практический интерес системах импульсные характеристики обычно имеют главный всплеск и незначительную протяженность во времени (рис. 3.1). В качестве f (t - to) можно выбрать такую зависимость, которая хорошо бы совпадала с hif) лишь на том интервале времени, где сосредоточена основная энергия переходного процесса.

Наиболее удобно выбрать гармоническую зависимость

/(f~g=cos(o(-g. (3.9)

Хотя функция (3.9) является неограниченно протяженной во времени, фактически сравнение ft (t) будет производиться лишь е одним или несколькими полупериодами. При этом возникает одна

трудность,. связанная с тем, что интеграл j cos и (/ - t) dt = оо

о

расходится и выражение (3.4) обращается в нуль. Чтобы устра нить это затруднение, бесконечно протяженную косинусоиду можно заменить достаточно большим числом ее периодов. При этом бесконечный верхний предел интегрирования будет заменен конечным

Г = 2яп/сй, (3.10)

где п - число периодов. Тогда выражение (3.4) можно переписать в следующем виде:

т

\ h{t)cosm{t-to)dt R ( . h, Т) = , ° / . (3.11)

W (t)]dt [ со& (Л if -to) dt

Для любого конечного значения частоты, вследствие быстрого затухания h{t), всегда можно выбрать такое число периодов п, чтобы разность

т

J h (t) cos fi) ( - Q dt - J n (t) cos fi) ( - Qdt\<e (3.12)

получилась сколь угодно малой. Учитывая сказанное, верхний предел интеграла, стоящего в числителе выражения (3.11), не внося заметной погрешности, можно заменить бесконечным. Вычислив далее величину интеграла

2я/г/и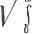

J COS* со ( - to) dt = пп/и

и приняв во внимание, что в процессе исследования число периодов п и дисперсия

ol=lhit)]dt = const

о

остаются неизменными, окончательно запишем

(О cos ait - to) dt [ h (t) e- - dt

R (fi), to) = -77==-= Re

V cl (jw/co) у cl (itn/ro)

= Re (K ejmH {Ml V). (3.13)

Здесь, как и ранее, Я (/со) - спектральная функция переходной характеристики исследуемой системы.

2* * 35

2. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ УСТАНОВЛЕНИЯ И ЗАПАЗДЬвВАИИЯ

Выражение (3.13) позволяет оценить качество совпадения аппрокси мирующей функции (3.9) с исследуемой импульсной характеристи кой. Для обеспечения лучшего совпадения можно смещать коси нусоиду во времени, меняя произвольный временной сдвиг 4, а так же изменять ее период соответствующим изменением частоты со. О качестве совпадения можно судить по величине получающихся значений выражения (3.13). Максимумы его будут соответствовать наилучшему совпадению h(t) с одним или несколькими полупериодами косинусоиды. Отбрасывая постоянные, не влияющие на положение экстремальных точек, сомножители, можно записать

R (со, / ) = Re [ й e j(MH (/(о)] = Re [ ]/ш е'<к (/ш)] =

= У^К (О)) COS + ф ((0)], (3.14)

где

К{а>) = \1< (/(0) I; ф (со) = arg К (/со) (3.15)

- частотная и фазовая характеристики исследуемой системы.

Так как выбранная функция f {t - tf) (3.9) содержит две произвольные величины 4 и (О, то и/ ((0, 4) является функцией этих переменных. Поэтому условие наилучшего совмещения h (t) с f {t- t) соответствует точкам полных максимумов (3.14) при изменении обеих переменных. Одним из условий максимума являете

cos[(o/p-1-ф((о)] = 1, откуда t = 2ntn/(i) - ф((о)/и. (3 16)

Другое условие при этом определяется из выражения

д1д(й[]а>К{(и)] = 0.

Однако вследствие того, что при возведении функции в степень положение ее экстремальных точек не меняется, гораздо удобнее пользоваться условием

d{(D[K((ii)V}dtii=0. (3.17)

Рассматривая процесс совмещения косинусоиды с импульсной характеристикой при постепенном увеличении частоты и, начиная от нуля, легко убедиться, что первый максимум R (и, Q соответствует наилучшему совмещению главного всплескаЛ' (t) с одним полупериодом косинусоиды (рис. 3.2). Несмотря на то что форма главного всплеска h (t) может довольно существенно отличаться от формы полупериода косинусоиды, их продолжительности будут отличатьс'я незначительно. Отклонение длительности полупериода / (Г-t) от длительности главного всплеска ft(О неизбежно должно повлечь уменьшение их взаимной корреляции, т. е. привести к уходу от точки максимума, но длительность главного всплеска h{t) определяет время установления переходной характеристики h (t), следовательно, при выполнении условий (3.16) и (3.17) длительность полупериода косинусоиды может служить критерием для оценки времени установ-

ления переходной характеристики. Можно также приближенно при-нятЬ этот полупериод косинусоиды в качестве аппроксимации глав- яого всплеска импульсной характеристики. Тогда интеграл t

(0-2 J cos - = [1 + sin (Oi it - Q]

(3.18)

явится аппроксимацией фронта переходной характеристики (рис. 3.3), а входящая в данное выражение частота со, является наименьшим положительным корнем уравнения (3.17). Длительность полупериода косинусоиды при и = ©1 равна времени нарастания фронта аппрок-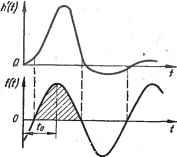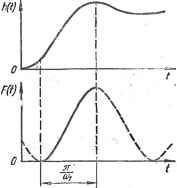

Рис. 3.2. Совмещение h(t) с полупериодом косинусоиды

Рис. 3.3. Аппроксимация фронтальной части h(t) отрезком синусоиды

симирующей функции я)) (f) от нуля до ее максимального значения. Это время нарастания (время установления)

t; = n/(ui (3.19)

отличается от используемого на практике отсчета времени установления на уровнях 0,1 и 0,9. Обращаясь к выражению (3.18) и производя отсчет на указанных уровнях, получаем

ул; 1,85/сй1. . -(3.20)

Это соотношение можно принять в качестве окончательного для приближенного вычисления времени установления.

Абсцисса вершины косинусоиды 4 соответствует времени запаз-; дывания переходной характеристики при отсчете последнего на уровне 0,5. Для вычисления времени запаздывания в выражении (3.16) следует, принять т - 0. Тогда окончательно можно записать

f, = -Ф((й1)/Ш1, (3.21)

Тде со = ©1 потому, что запаздывание также должно определяться лри одновременном выполнении условий (3.16) и (3.17). Знак минус

необходим в этой формуле потому, что используется представление

и, следовательно, фазовая характеристика при такой записи имеет отрицательный угол наклона и сама принимает отрицательные значения. В заключение составим рецепт для практического применения методики приближенного вычисления времени установления и запаздывания. Прежде всего, необходимо получить выражение амплитудно-частотной характеристики К. ((о) исследуемой системы и составить уравнение (3.17). Далее, вычислив наименьший положительный его корень, с помощью выражения (3.19) или (3.20) и (3.21) находят ис-*комые величины. Таким образом, для вычисления времени установления и запаздывания необходимо лишь знание частотной и фазовой характеристик исследуемой системы и вычисление наименьшего положительного корня (3.17).

В случае систем с сосредоточенными параметрами, когда передаточная функция (амплитудно-фазовая характеристика) /((/ю) выражается рациональной дробью полиномов по степеням /ю, условие (3.17) обращается в алгебраическое уравнение, степень которого равна сумме степеней числителя и знаменателя передаточной функции. Хотя степень этого уравнения может оказаться весьма высокой, значение наименьшего положительного корня можно найти приближенно известными способами. Во всяком случае, найти один только наименьший положительный корень уравнения (3.17) всегда значительно легче, чем определить все корни (и притом часто комплексные) характеристического уравнения.

Анализ уравнения (3.17) показывает, что для реальных физически осуществимых систем выражение

]/№/<(©) (3.22)

при значениях ш - О и со = со обращается в нуль, оставаясь неотрицательным при остальных значениях частоты. Поэтому в интервале частот О < (О < схз оно имеет по крайней мере один максимум. Иначе говоря, задача отыскания условия наилучшего совпадения h{t) с косинусоидой всегда имеет хотя бы одно решение. Описанные свойства и непрерывность выражения (3.24) свидетельствуют о том, что оно всегда может иметь только нечетное число экстремальных точек. Первым в направлении возрастания частоты всегда располагается максимум, все нечетные экстремальные точки также являются максимумами, а четные минимумами. Случай кратных корней также можно подвести под это правило. При нечетной кратности корня точка соответствует максимуму или минимуму, в зависимости от того,-за каким по счету предьщущйм корнем она следует. При четной кратности точка соответствует перегибу кривой (3.22) с горизонтальной касательной и, следовательно, не является экстремальной. Четная кратность не нарушает дальнейшего чередования корней, так как несколько их пар просто не участвуют в чередовании максимумов и минимумов.

Еели уравнение (3.17) имеет только один положительный корень, то им и определяются величины времени установления и запаздывания. Случай нескольких корней свидетельствует о более сложном характере исследуемой переходной характеристики, в частности, о наличии на ней наложенных колебаний, частота которых близка к значениям последующих нечетных положительных корней. Наименьший из положительных корней при этом может определять общую продолжительность переходного процесса либо время установления. При наличии нескольких положительных корней целесообразен более тщательный анализ. В частности, определенным критерием может служить значение ординаты частотной характеристики К. (со) в точке, соответствующей первому корню. Если при нормированной по вертикальной оси частотной характеристике значение этой ординаты превышает значение 0,6 ...0,7, то корень определяет время установления. При меньших Значениях ординаты результат становится ненадежным. В последнем случае необходимо бэлее тщательное исследование. В системах, содержащих звенья с распределенными параметрами, может оказаться бесчисленное множество положительных корней. Это свидетельствует о том, что импульсная характеристика состоит из нескольких частей, разнесенных во времени. Первый корень в этом случае, как правило, определяет общую продолжительность переходного процесса.

О точности определения параметров переходного процесса описываемым методом можно судить по остроте экстремумов выражения (3.22), т. е. чем острее и чем выше экстремум, тем лучше совпадение к (t) с f{t -tn) и точнее фиксируется его момент, а значит выше и точность вычислений. Более строгая количественная оценка погрешностей вычисления параметров переходного процесса будет изложена ниже.

Примеры.вычисления времени установления и запаздывания

Наиболее наглядное представление о точности и быстроте получения желаемых результатов с помощью описываемого метода дает рассмотрение практических примеров.

Пример 1. Рассмотрим систему с простейшей передаточной функцией вида

/С (/со) = 1/(1-1-/сот/,

которой является /г-каскадиый усилитель на резисторах. Для удобства и общности анализа введем понятие безразмерной нормированной частоты х = ит, после чего можно записать

к (jx) = 1/(1 -f- jxf или [К (x)P = 1/(1 -f- хТ и ф (X) = - п arctg х.

Составив уравнение (3.17) и взяв производную по х, получим х^ (2п - 1) - - 1 = 0, отауда

Х1 = ш,Тз= 1 2П-1;

<з/Тл = ф (xj)/xi=rtl/ 2n - 1 arctg (l/l/ 2n - 1); ly/x= l,85.jci= 1,85121.

(3.23)

При достаточно большом числе каскадов (и > 3) выражения (3.23) стремятся к известным зависимостям

3 ~ Тв. <у 2,62 Уп%а-

в табл. 2 приведены значения времени установления н запаздывания, вычисленные с помощью выражения (3.23), а также для сравнения указаны их величины, полученные непосредственно из переходных характеристик.

2. Время установления и запаздывания в миогскаскадном усилителе

Приведенная таблица показывает, что точность приближенного вычисления параметров переходной характеристики получается вполне приемлемой и повы-(цается с увеличением числа каскадов. Наибольщую погрещность имеет одиночный каскад ( = 1), так как его импульсная характеристика (имеющая экспоненциальный характер) по своей форме наиболее сильно отличается от полупериода косинусоиды. При этом качество совпадения, а следовательно, и точность оказываюадя низкими. У многокаскадных усилителей импульсная характеристика ближе по форме к полупериоду косинусоиды, что и обусловливает более высокую точность. Этот пример подчеркивает особую пригодность описываемого метода для анализа многокаскадных систем.

Пример 2. Рассмотрим систему с передаточной функцией вида

к их) = [(1 + jkx)/(l + jx - hx)r,

примером которой является многокаскадный усилитель с простой высокочастотной коррекцией. Составив выражения частотной и фазовой характеристик

[К (х)]= = {(1 -f fe,V)/[(l - Кх) + х']Г

и

Ф (х) = п arctg kx - п arctg [х/(1 - kx)], где ki - коэффициент коррекции, в соответствии с формулой (3.17), получим

й*(2п - 1) + З/г^ (2п - 1 + i) X*- - [{l~k) + 2nikl+2k-l)]x~l=0. - (3.24)

Результаты вычислений корня этого уравнения для однокаскадного усилителя (п = 1) при различных величинах коэффициента коррекции ki приведены в табл. 3. Там же указаны значения времени установления и запаздывания, найденные описываемым методом и непосредственно попереходным характеристикам. Особенностью приведенных вычислений времени установления является лишь то, что корреляционный метод дает отсчет его на уровнях 0,1 и 0,9 не от установившегося значения, а от максимального. Указанное обстоятельство учтено и при непосредственном отсчете по переходным характеристикам.

Рассматриваемый случай одиночного каскада также является весьма неблагоприятным с точки зрения качества совмещения h{t) с полу-

3. время установления и запаздывания в усилителе с простой высокочастотной коррекцией

периодом косинусоиды. Но и при этом погрешность вычисления времени установления и запаздывания получается сравнительно небольшой. Для многокаскадного усилителя она должна быть соответственно меньшей. В табл. 4 приведены результаты расчета Бремени установления для многокаскадных усилителей с -простой коррекцией при

4. Время установления в многокаскад.чом усилителе с простой высокочастот.чой коррекцией

различных значениях коэффициента коррекции ki. К сожалению,-их нельзя сопоставить с точными значениями, так как последние получить практически невозможно. Что же касается описываемого метода, то для .многокаскадного усилителя достаточно лишь в уравнение (3.24) подставить соответствующее значение числа каскадов п.

3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ВЫБРОСОВ

. Важным, параметром переходной характеристики является величина выбросов (перерегулирование). В случае немонотонной переходной характеристики импульсная характеристика, как ее производная, оказывается знакопеременной (рис. 3.4). При этом площадь каждого отрицательного участка импульсной характеристики h (t) численно равна разности ординат соседних максимума и минимума переходной характеристики. Иначе говоря, площадь каждого отрицательного участка импульсной характеристики равна величине, суммарного (положительного и отрицательного) выброса. Кроме того, площадь части импульсной характеристики, расположенной ниже горизонталь-

ной Оби, равна общей сумме всех выбросов. Следовательно, величина этой площади является мерой последовательности всех выбросов. Поскольку в большинстве случаев нежелательным является не только наличие первого выброса, но и выбросов вообще, то оценка суммарных выбросов может явиться достаточно надежным критерием качества переходного процесса. К тому же очень часто, вследствие быстрого затухания переходного процесса, наибольшую величину имеет лишь сумма первых положительного и отрицательного выбросов, а последующие выбросы оказьюаются относительно малыми. При этом сумма всех выбросов будет мало отличаться от величины их первой пары.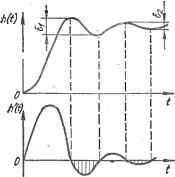

Рис. 3.4. К определению величины выброса по импульсной характеристике немонотонного переходного процесса

Рис. 3.5. Совмещение импульсной характеристики h(t) с колебаниями прямоугольной фор-

Если сравнить площади, ограниченные кривыми \h(t)\ и h{f), то в соответствии с изложенным можно определить суммарную величину всех выбросов, так как разность этих площадей будет равна удвоенной площади отрицательной части импульсной характеристики:

00 00 00

5] в = I [ JI А' (О I dt - j h (t) dt] = i [ j I h (t) \dt~l

(3.25)

Модуль импульсной характеристики можно получить, если h{t) умножить на некоторую функцию F (/), представляющую собой в общем случае непериодические колебания прямоугольной формы с единичной амплитудой, точки изменения полярности которых в точности совпадают с нулями исследуемой импульсной характеристики. На практике, однако, определить такую функцию будет чрезвьмайно трудно. Поэтому для приближенного определения модуля целесообразно использовать в качестЬе функции f {t) периодические колебания прямоугольной формы, наилучшим образом совмещенные с исследуемой импульсной характеристикой (рис. 3.5). Для определе1ия условия наилучшего совпадения этих кривых также можно воспользоваться оценкой вида (3.4), аналогичной определению максимума функ-