ции взаимной корреляции. Причем и здесь F (f) следует ограничить достаточно большим целым числом периодов п. Не повторяя приведенных выше рассуждений [см. (3.9) - (3.12)] и представив F (t) в виде тригонометрического ряда

л 2п -1

. после соответствующих преобразований можно записать

(О = ~ S -5- (2 - 1) ( - д. (3.26)

[h(t)]dt 1 [f

(2n-l)

(3.27).

где А - константа. Далее следует определить условие, наилучшего совмещения прямоугольных колебаний с h{t) по максимуму R (п/Т, to). Строгое решение этой задачи, к сожалению, практически невозможно. Поэтому приходится ограничиться лишь приближенным решением. В первом приближении можно использовать только первый член суммы (3.27). В этом случае условия максимума Ц (п/Т, to) окажутся тождественными с условиями (3.16) и (3.17), так как само выражение (3.27) обращается в (3.12). Следовательно, найденные ранее значения (Oi= n/Ti и 4 могут также использоваться в качестве приближенных условий максимума (3.27).

Пользуясь известными методами, можно было бы найти соответствующие поправки к вычисленным приближенным значениям Ti и to. Однако в этом нет необходимости. Во-первых, ряд (3.27) является абсолютно сходящимся и сходится быстро. Действительно, уже само значение ©1= jx/Ti приходится на область спада частотной характеристики /( (й). Первый же из отбрасываемых членов/( ((3n;/7i)x X cos [3nlTito + ф (3n;7i)]}/3 обычно оказывается значительно меньше оставляемого, так как значение только одного сомножителя К. (Ззг/Ti) приходится на область частотной характеристики с очень малыми ординатами. Следовательно, отбрасываемые члены не могут оказать сколько-нибудь сущестЕенного влияния на пслсженйе экстремальных точек (3.27). Во-вторых, при получающейся замене прямоугольных колебаний косинусоидой и при определении условий (3.16) и (3.17) нули косинусоиды будут располагаться вблизи нулей импульсной характеристики. При этом важно обеспечить хорошее совпадение нулей лишь на том временном интервале, где сосредоточена основная энергия переходного процесса (рис. 3.5).

Поэтому Б качестве условий максимума (3.27) можно использовать условия (3.16) и (3.17). Однако, за счет неточного совпадения ну-

лей h{t) и F (t) величина интеграла J h{t)F {t) dt получится несколь-

ко меньшей площади ограниченной кривой \h(t)\, а значит, и суммарная величина всех выбросов будет найдена с недостатком. Поэтому . можно считать, что выражение (3.25) дает не суммарное значение всех выбросов, а только величину их первой пары.

Итак, определив из условия (3.17) значение частоты ец и вычислив с помощью (3.21) смещение 4= 4. можно найти период колебаний 27 = 2n/(Bi и, приняв во внимание (3.26), записать

h (t) F (t) dt=± S W=T - 1) il cos [Ф [(2n - 1) (0,1.

-(2п-1)ф((о,)}, . a затем определить и величину выбросов

... со -

e[h(t)F(t)dt-l = .

О

- = 4 S ё=Т t(2n- 1) (oJ cos [ф [(2п - 1) coj -

-(2п~1)ц>(щ)}~1. (3.28)

Входящий в формулу (3.28) знакопеременный ряд для физически осуществимых систем сходится не медленнее, чем 1/(2п - 1), а во многих случаях значительно быстрее, т. е. является абсолютно сходящимся. Быстрая сходимость ряда (3.28) позволяет ограничиться для практических вычислений всего лишь одним-двумя первыми членами. При использовании двух членов для выброса получаем формулу

Е^2{К Ы - (1/3) К (3c0i) cos [ф (Зщ) - Зф (со,)] -.(1 /2)}/я, (3.29)

которая также будет давать значение выброса с недостатком. Если же ограничиться одним лишь первым членом, то получается исключительно простая и удобная формула

e[4/<-((0i)/n-1]/2. (3.30)

Последнее выражение дает величину выброса с избытком. При этом избыток будет частично компенсировать недостаток, обусловленный неточностью совпадения нулей.

Использование формулы (3.30) особенно удобно и обеспечивает высокую точность Б случае систем, представляющих каскадное соединение звеньев с одинаковыми частотными характеристиками. Ти-

пичным примером таких систем являются многокаскадные усилители; В этом случае ряды (3.27) и (3.28) сходятся особенно быстро.

При вычислении выбросов по формулам (3.29) или (3.30) следует иметь в виду, что для монотонных переходных процессов

00 00

о о

т. е. значения выбросов, определяемые по этим формулам, получатся отрицательными. Если вычисленная величина выброса оказывается отрицательной, то это свидетельствует о, монотонном характере переходного процесса и об отсутствии выбросов.

При определении величины выброса с помощью формулы (3.29) или (3.30) получается абсолютная ошибка, обусловленная неточностью совпадения нулей h(t) и F (t), а также отбрасьгоанием высших членов, ряда (3.28). В случае меньших значений выбросов одна и та же абсолютная ошибка дает большую относительную погрешность. Кроме того, малые выбросы часто требуется определять с более высокой точностью, чем большие.

Для повышения точности вычисления малых выбросов можно прибегнуть к следующему приему: искусственно увеличить выбросы исследуемой переходнойхарактеристики в известное число раз. Так как выбросы располагаются в более удаленной от начала координат части переходной характеристики, увеличение их масштаба удобно осуществить, вводя дополнительный экспоненциальный множитель к исследуемой импульсной характеристике

. . ha{t)==h{t)e t, . (3.31)

где а - некоторый постоянный положительный коэффициент.

Рассматривая вместо h{t) новую зависимость (3.31) и используя теорему о смещении в комплексной области, передаточную функцию исследуемой системы можем записать в виде

к = к{1<л~а). (3.32)

Коэффициент h следует выбирать так, чтобы сохранялась абсолютная интегрируемость выражения (3.31), т. е. чтобы интеграл

h {f)t dt<.M. имел ограниченную величину. Для этого, воспользовавшись известным соотношением

lim Г/г'(0

dt = lim к (/£0 - й) == /С (/(0) /со= ,

необходимо проследить, чтобы при непрерывном увеличении а, начиная от нуля и вплоть до выбранного значения, выражение (/(о) /м=-й нигде не обращалось в бесконечность. В.. противном случае условие абсолютной интегрируемости не будет соблюдено.

и потребуется соответственно уменьшить выбранное первоначальное значение коэффициента а.

Для вычисления выброса далее необходимо определить модуль и фазу новой передаточной функции (3.32), составить по аналогии с (3.17) уравнение 5 [со /<(/<о -с) Р]/(о = О, найти наименьший его полой^ительный корень и вычислить с помощью (3.30) выброс функции (3.31) е'. При этом в (З.ЗО) вместо /<( ) следует подставлять 1/С(/{о - а)\. Чтобы найти истинную величину выброса е, следует снова ввести поправочный множитель

E = se-, (3.33)

где 1г- абсцисса первого экстремума переходной характеристики. Момент времени складывается из времени запаздывания (3.21) и половины времени установления, отсчитываемого по нулевой и максимальной ординатам (3.19),

= 4 4- 1/2у = -ф (oJ/Oi + n/2cOi = М' - Ф (3.34)

С учетом последнего соотношения для уточненного выброса исследуемой системы получим

е = se-°W2-4< )3/ >. (3.35)

Примеры определения выбросов переходной характеристики

Для иллюстрации результатов, полученных при пользовании описанной методикой, в табл. 5 приведены расчетные и истинные значения выбросов одиночного каскада усилителя с простой высокочастотной коррекцией. Расчет выбросов при различных величинах коэффициента коррекции выполнен по формулам (3.29) и (3.30). Истинные значения выбросов найдены по точному выражению переходной характеристики и даются для сравнения.

6. Величины выбросов в усилителе с простой высокочастотной коррекцией

Приведенные дайные показывают, что точность вычислений выбросов получается достаточно высокой. Причем, она вполне может удовлетворить запросы практики и при использовании простейшей формулы (3.30). Только в области очень малых выбросов относительная (но не абсолютная) погрешность становится значительной. Так, в частности , при ky= 0,33 с помощью выведенных формул выброс обнару жить не удается, тогда как в действительности имеет место выб'-рос 8 = 0,75 %.

Применяя описанный прием уточнения выброса, для передаточной функции получим

(1-M)+Mfei

KUx-a)

(I - а + к^а^) + jx (1 - 2feia).+ ijxf kt

Подставив значение fe, = 0,33, выбрав а = 0,75 и определив модуль К {jx-о), из условия (3.17) находим = 1,07. Далее, с помощью (3.29) определяем е'=> = 0,085. Наконец, с помощью (3.35) получаем

Е = о,085е-(-5/ ->< 2+1-02 = 0.014.

При использовании уточненной методики выброс обнаруить уже удается и его величина оказывается значительно более близкой к истинной. Такой же расчет, проделанный д я fe = 0,25 и при выборе с = 1. дает Xj= 0,608, 6= = -0,05, т. е. при критическом значении коэффициента коррекции ki выброс, как и следовало ожидать, отсутствует.

4. вычисление параметров переходного процесса по графически заданной частотной характеристике

В инженерной практике довольно часто приходится встречаться с графическим представлением частотных характеристик исследуемых систем. Особое значение при этом приобретают частотные характеристики, снятые экспериментально. В большинстве случаев снять частотную характеристику исследуемой системы значительно проще, чем переходную. Поэтому целесообразно рассмотреть методику определения параметров переходных процессов по графически заданным частотным характеристикам.

В отличие от существующих способов, распространение корреляционного метода на случай графического представления частотных характеристик позволяет исключительно просто решить поставленную задачу. При этом определение важнейших параметров - времени установления и выбросов - может производиться непосредственно без каких-либо промежуточных вычислений. Больше того, если частотную характеристику системы можно представить в виде

Хобщ((о) = [/СИ] , (3.36)

где К (ю) - частотная характеристика отдельного звена, то параметры переходного процесса при произвольном числе звеньев можно найти по частотной характеристике одиночного звена. Примером таких систем являются многокаскадные усилители.

При частотной характеристике вида (3.36) уравнение (3.17) для определения условия наилучшего совмещения h(t) и / (/- 4) можно представить как

а(Кй[А:((о)П5(о = 0. (3.37)

Такая запись не нарушает общности выводов, так как для любых других систем, не удовлетворяющих форме записи (3.36), можно просто считать n = 1 и вместо /С (со) подставлять Кобщ (со). V Если /( = /( (со) рассматривать не как частотную характеристику, а как некоторую функцию независимой переменной со, то выражение (3.37) будет представлять собой дифференциальное уравнение, общий интеграл которого запишется в виде

]/Ml/j ==C = const или /С = С/1. (3.38)

Вернемся теперь к решению уравнения (3.37) для исследуемой частотной характеристики. Выполнив дифференцирование и произведя соответствующие преобразования, получим уравнение

((о) = 2псй {дК {(о)/д(о). (3.39)

Тогда графически решения будут представлять точки пересечения частотной характеристики /((со) с кривыми - 2 (о(5/С((о)/5(о). Но и все интегральные кривые вида (3.38) таюке удовлетворяют уравнению (3.37). Следовательно, решения будут обш,ими точками для частотной характеристики и кривых (3.38). Легко убедиться, что в этих точках угол наклона касательных к частотной характеристике и к соответствующей кривой (3.38) одинаков. Действительно, из (3.39) находим

К ((Of) tu==tu. 2n(uf

причем равенство выполняется только в точках, соответствующих одному Из корней (О = (О,-. Для кривых (3.38) получаем

дК/да = д (C/Yм)/(о = -с/(2псо > й) .

Но в точке, соответствующей корню со = со,., С/у^со =(со,.), и, следовательно,

дК1д(й со=со,- = -С/2псо,1>й. = -К ((о.)/2псо.,

т. е. производные в точках со = со оказываются равными.

Итак, решениями уравнения(3. 37), определяющими условия наилучшего совмещения/!(/) и / ( - 4), являются точки касания частотной характеристики f{ (со) с кривыми семейства (3.38). Если частотную характеристику и кривые (3.38) построить в логарифмическом масштабе по обеим осям (рис. 3.6), то кривые семейства (3.38) превратятся в параллельные прямые с угловым коэффициентом

tgcx = -1/2п. (3.40)

Уравнение (3.37) можно решить, прикладывая линейку к частотной характеристике под соответствующим углом.

Таким образом, при графическом задании частотной характеристики положительные корни уравнения (3.17) или аналогичного уравнения (3.37) непосредственно определяются по точкам касания частотной характеристики с семейством параллельных прямых, если по обеим осям величины отложены в логарифмическом масштабе (рис. 3.6).

По горизонтальной оси, кроме частоты , можно отложить в соответствующем масштабе величины времени установления, которые связаны с определяемой частотой со = coi соотношением ty- l,85/coi~0,3 i. Построение этой шкалы также показано на рис. 3.6. При этом определив, как указывалось выше, абсциссу точки касания, можно непосредственно считывать величину времени установления без каких-либо промежуточных вычислений.

Ординату, точки касания, равную К (/i). можно использовать для определения выбросов, с которыми она связана соотношением

в={4/я[К(Ь)Г-1}/2. . (3.41)

Так как это выражение непосредственно связывает ординаты частот характеристики с величиной выброса, его можно использовать для построения на вертикальной оси шкалы, позволяющей по ординате точки касания непосредственно.определять выброс. Правда, для каж-

2 iB

0.9 0.8 0.7 0.6 0,5

BO 50.

- 40

- 30

10 5 0

0,05 0,07 qi 0,2 0,3 0,4 0,5 0,7 1 -2 3 4 5 7 101=Х/2Г

I-I-1--1-! L I I I I I I I L I I I I I I I l J I

5 4 3 Z 1.5 1 0,7 0,5 Ofi 0,3 0,2 0,15 0,07 0fl50fi4 0J33 tg

Рис. 3.6. К определению параметров переходного процесса по заданной частотной характеристике

дого значения п необходимо строить свою шкалу, что создает некоторые неудобства. На рис. 3.6 показан пример построения в логарифмическом масштабе по обеим осям семейства прямых вида (3.38), а также шкалы выбросов для случая п- 1. По этому же графику можно определить координаты точки касания и время, установления при произвольном числе каскадов п, для чего необходимо лишь в соответствии с формулой (3.40) изменить наклон прямых. Для определения выброса необходимо либо построить серию шкал для разных п,либо воспользоваться другим приемом: В частности, удобно пользоваться графиком переюда (рис. 3.7), позволяющим по ординате в точке касания /( (/i) определить величину выброса.

Итак, распространяя корреляционный метод на случай графического представления частотной характеристики исследуемой системы, можно производить непосредственный отсчет времени установления и выбросов, не прибегая к промежуточным вычислениям.

Вследствие того, что графический метод оказывается удобным при анализе переходных процессов в многокаскадных системах с идентичными частотными характеристиками отдельных каскадов, целесообразно определять условия, при выполнении которых выбросы не будут превышать заданной величины. Для этой цели необходимо построить кривые постоянных выбросов и сопоставить их с частотной характеристикой исследуемой системы.

Воспользовавшись выражением (3.41) и разрешив его относительно ординаты частотной характеристики одиночного каскада, получим

К = V (я/4)(1 -Ь28) = Л!/ ,

(3.42)

где Л = (я/4)(1 -f 2е). Хотя для реальных систем физический смысл имеют лишь целые значения допустим на время, что п может изменяться непрерьгоно, принимая любые значения п^1. Тогда на основании (3.42) можно сч итать, что ордината К, соот-вщ) ветствующая заданной величине выброса, является не-Рис. 3.7. График для расчета величины вы- ппепр,тнпй *VHK77Heu К-ппни бросов при различном числе каскадов уси- ПрерьГОНОИ функцией . КОрнИ

лителя уравнения (3..37), определяе-

мые по точкам касания частотной характеристики с кривыми (3.38), будут непрерывно меняться при изменениях п. Следовательно, через переменную п можно выразить абсциссы и ординаты гипотетической частотной характеристики, которая при любом п обеспечивает заданную величину выброса е. Для ординат такой характеристики уже получено выражение (3.42). Для определения же абсцисс необходимо, чтобы каждая ордината (3.42) находилась в точке касания с соответствующей кривой (3.38), т. е. необходимо, чтобы выполнялись условия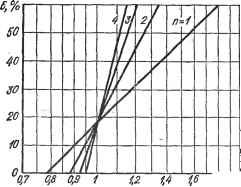

дК1дт = -C/2naV( = -К/2п(о.

(3.43)

Составим выражение производной зависимости абсциссы точки касания от величины п и преобразуем его к виду

. да,/дп = (да/дК) (дК/дп) = (дК/дп)/{дК/д(о).

Тогда, подставляя значения производных дЮдп и дК/да, определяемые соответственно из (3.42) и (3.43), окончательно находим du)/dn = 2(i)]nA/n, откуда = е^л inn

Так как при и = 1 ю = (Oi и /< (01)-= А, то, подставляя эти значения, находим постоянную интегрирования Ci= 1/coi, а после со-

ответствующих преобразований и исключения переменной п записываем

In /С = In Л (со/и1)/2 пл. (3.44).

Это и есть выражение гипотетической частотной характеристики, обеспечивающей при любом п заданную величину выброса .Для сопоставления ее с исследуемой частотной характеристикой одиночного каскада необходимо совместить точку, соответствующую интересующему нас целому значению п (рис. 3.8) с исследуемой частотной характеристикойi((o). При совмещении кривые (рис.3.8) следует сдвигать вдоль горизонтальной оси, но так, чтобы значения ординат этих кривых и частотной характеристики совпадали. Если в точке совмещения частотная характеристика проходит более полого, чем кривая (3.44), то это значит, что точка касания для данного п располагается ниже. Следовательно, ордината меньше ординаты кривой (3.44) при данном значении п, а значит и выброс будет меньше того, для которого рассчитана используемая кривая (3.44). Если частотная характеристика проходит круче, то точка касания расположена выше и выброс будет больше указанного. Приве-, денные рассуждения основываются на том, что кривые (3.44) в любой своей точке касательны к кривым семейства (3.38) для соответствующего значения .Используя последнее свойство кривых (3.44), можно поступать и иначе. Перемещая соответствующую кривую (рис. 3.8) параллельно самой себе, добиваются ее касания с исследуемой частотной характеристикой в точке, соответствующей выбранному . Если ордината точки касания К. (©i) меньше ординаты кривой (3.44), то и выброс будет меньше указанного.

Кривые (рис. 3.8) позволяют определить, является ли выброс в многокаскадной системе большим или меньшим критического. Для этого сначала по частотной характеристике одиночного каскада необходимо найти значение со == 1 и величину его выброса е. Затем, совместить точку для п - 1 кривой (3.44), выброс которой равен найденному, с точкой о ~ oi частотной характеристики. Если частотная характеристика проходит ниже этой кривой и ее наклон при одинаковых значениях ординат не больше чем у кривой (3!44), то выброс в системе будет меньше критического. Иначе говоря, величина выброса с увеличением числа каскадов будет снижаться.

На рис. 3.8 построены кривые (3.44) для значений выбросов е < 13,5 %, при которых Л < 1. Исследование многокаскадных систем с такими.выбросами представляет наибольший интерес. Можно построить аналогичные кривые- и для больших выбросов. Следует

Рис. 3.8. Кривые

БЫб]ЭОСОБ

постоянной величины

лишь отметить, что область их определения при интересующих нас значениях п >1 будет (o/(Oi> 1 и > 1. Это находится в согласии с тем, что пучок прямых равных значений п пересекается в точке с координатами cu/toi= 1 и = 1 и имеет положительный наклон. Методика пользования кривыми для е > 13,5 % остается прежней. Необходимо только подчеркнуть, что из самого характера построения кривых для е> 13,5 % следует ограничение возможных величин критических выбросов. Последние не могут превышать 13,5 %.

5. приближенное вычисление переходных характеристик

Помимо определения параметров переходного процесса, нередко необходимо иметь полную картину протекания переходного процесса. При этом в каждом конкретном случае требуется вполне определенная точность вычислений.. Наиболее ценным окажется тот метод, который позволит получить любую точность и дает возможность оценить погрешности вычислений. Излагаемый ниже метод выгодно отличается, от существующих тем, что при значительно меньшей затрате труда обеспечивает высокую, наперед заданную точность расчетов, а также позволяет просто оценить погрешности.

Описываемый метод основывается на интегральном представлении переходной характеристики исследуемой системы через ее импульсную характеристику

- h (О = J h (т) dx. - (3.45)

Если импульсную характеристику А'(т) умножить на некоторую функцию / (т), представляющую собой прямоугольный импульс с единичной амплитудой и длительностью t, то, не меняя величины интеграла (3.45), можно его верхний предел сделать бесконечным:

h{t)\h (%)f(x)dx. (3.46)

Поскольку интегрирование ведется от нуля в сторону положительных значений т, описываемьй функцией / (т) прямоугольный импульс может быть продолжен в сторону отрицательных величин т. Соображения удобства последующих выкладок делают целесообразным использование в качестве f (т) импульса длительностью 2t, симметричного относительно начала координат (рис. 3.0). Если обратиться к спектральному представлению этого импульса .

/(т)= -i- f [(sm(o/)/(o]e/ dco,